 |
||
Определение параметров регуляризации в задачах построения моделей систем прямыми измерениями входных и выходных сигналов
Р.И.Ивановский
Санкт-Петербургский Государственный технический университет
Abstract - The author considers a choice of parameters of calculations in one of incorrect problems of creation of model of dynamic system. The initial data for creation of model are the input and output signals of system. The example of such choice is given.
Широкий круг задач анализа и синтеза динамических систем в условиях неопреде-ленности априорной информации связан с необходимостью определения параметров динамических звеньев, в качестве которых могут выступать отдельные блоки объекта управления, управляющей части, вся систе-ма в целом. Подобная проблема возникает, в частности, при разработке математических моделей систем и их фрагментов по полученным реакциям на известные входные воздействия [1].
В этих задачах определению подлежат параметры аппроксимирующего выражения, заданного в одной из взаимосвязанных форм: в виде передаточной функции, систе-мы дифференциальных уравнений,
z-пере-даточной функции, разностных уравнений.Среди множества подходов к решению подобных задач выделим методы, позво-ляющие во временной области получить параметры (коэффициенты) каждой из пере-численных выше взаимосвязанных форм представления динамических звеньев. Выбор временной области объясняется уни-версальностью и простотой беспоисковых алгоритмов определения параметров, получаемых в результате. Основу таких алгоритмов составляют обычные операции линейной алгебры.
Рассмотрим особенности реализации процедур решения рассматриваемых задач на простом примере [2]. Пусть дискретное линейное динамическое звено n-го порядка представлено своими входным сигналом u и выходным сигналом y, значения которых определены через интервал дискретности Т. Пусть также z-передаточная функция звена имеет вид
W(z) = H1·(z•En - Ф1) - 1 • Г1; (1)
Ф1
=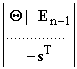 ; Г1 = M -1 d; H1 =
|10..0|;
; Г1 = M -1 d; H1 =
|10..0|;
M =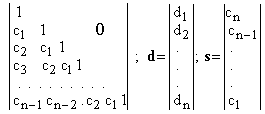 .
.
Неизвестные векторы
c и d содержат коэффициенты полиномов знаменателя и числителя W(z) соответственно. Нулевой вектор Q и матрица E имеют порядок (n –1). Каноническая реализация Rd1 = (Ф1, Г1, H1) с матрицами вида (1) может быть образована из любой другой полностью наблюдаемой реализации Rd = (Ф, Г, H) изменением ее базиса пространства состоя-ний с помощью собственной матрицы на-блюдаемости Nd реализации Rd [1, 2].Таким образом, имеем множество ре-зультатов измерений y
i , ui , i = 0,1,2, ... N, которое необходимо использовать для получения 2n элементов вектора g:gT = | - cT , dT | ; (2)
cT = | c1 , c2 , . . . cn |; dT = | d1 , d2 , . . . dn |
и передаточных функций W(p), W(z), а также матриц разностных и дифференци-альных уравнений. Процедуры пересчета элементов вектора
g в параметры других перечисленных выше форм представления динамического звена основаны на взаимно обратных преобразованиях, которые под-робно рассматриваются в [1, 2] и здесь опущены.Поставленная задача может быть решена с применением ряда подходов, относящихся к классу решений систем линейных алгебраических уравнений. Осно-вой этих подходов служит метод наимень-ших квадратов в форме обобщенного обра-щения матриц или в рекуррентной форме. Проблема существования решения и выбора допустимого вида входного сигнала в рассматриваемой задаче обсуждается в [2].
Для получения решения методом наи-меньших квадратов отметим, что входные и выходные сигналы звена, а также искомый вектор
g связаны очевидным соотношением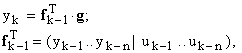 (3)
(3)
где вектор g имеет структуру (2).
Измеряя значения входных сигналов и соответствующей выходной реакции системы через q тактов (q = 1,2,3...), получаем систему L уравнений ( L ?
2n)![]() ; (4)
; (4)
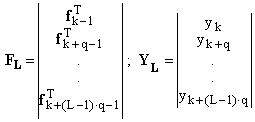 .
.
Решение системы уравнений (22) будем искать в виде
![]() , (5)
, (5)
где:
Известно, что задачи, аналогичные рас-сматриваемой, относятся к некорректным математическим задачам, в которых резуль-таты в сильной степени зависят от качества исходных данных, инструментальных ошибок компьютера, методических и трансформированных ошибок вычислений. К подобным задачам относится большинство задач
линейной алгебры, связанных с обращением плохо обуслов-ленных матриц, задачи регрессионного анализа, аппроксимации и т.д. В общем случае проблема решения некорректных математических задач не всегда сопряжена с возможностью выработки конструктивных рекомендаций по повышению достоверно-сти получаемых результатов. Общий случай рассмотрения таких задач выходит за рамки настоящего материала. Однако для рассмат-риваемой задачи могут быть рекомен-дованы некоторые практические приемы до-стижения и повышения точности решения. Это объясняется тем, что в задачах оценки параметров динамических систем по заданным входным и выходным сигналам имеются возможности для оценки досто-верности получаемых параметров путем сопоставления исходной информации с теми реакциями звена, которые получаются при найденных значениях параметров.Действительно, определяя вектор пара-метров
g и подставляя его оценку в один из этапов взаимно обратных преобразований [1, 2], можно получить, например, переход-ную характеристику звена с найденными параметрами и сопоставить ее значения с исходными (или с реакцией исследуемого звена на единичный скачок) на выбранном временном интервале или в отдельных точ-ках на оси времени. Такое же сопоставление может быть проведено и для других входных сигналов.Ниже без потери общности будем считать известной переходную характери-стику звена, для которого решается задача определения параметров в описанной постановке, а звено – устойчивым. Это означает, что известными являются установившиеся значения y(?) = p и значения у
k в отдельные моменты времени tk. Эти данные могут быть использованы для контроля качества получаемых оценок и выбора параметров регуляризации. Принципиально для контроля качества результатов и выбора параметров регуляри-зации в общем случае может быть исполь-зована любая унимодальная функция от разности ?y(?) между известным (или теоретическим) значением y(?) и значением p(g), полученным подстановкой в (4) результатов оценки вектора g. Однако функция от ?y(?) неприемлема для контроля качества результатов, например, при учете в алгоритме получения g допол-нительных данных в виде значений y(?) = p, поскольку получаемое вариацией e мно-жество вариантов решений будет характе-ризоваться как раз тем, что все решения имеют одинаковые установившиеся значе-ния переходных характеристик, равные р [2]. Поэтому функции этого типа могут использоваться для частичного контроля качества результатов лишь в задачах, в решении которых не учитываются известные y(?).Для контроля качества решений и выбора значений e могут применяться также и другие меры рассогласования полученных решений и исходных (или теоретических) данных, например функции от разностей в отдельных точках на оси времени, на совокупности таких точек в интервале наблюдения и т.д. Следует сказать, что оценка качества по отдельным точкам в диапазоне исследования звена не может служить основой для создания процедуры выбора параметров e . Такие оценки могут носить лишь локальный характер и использоваться для экспресс-анализа чув-ствительности решения к вариациям e
.При выборе параметра регуляризации e представляется целесообразным использо-вать интегральные критерии. Один из вариантов таких критериев имеет вид
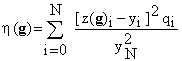 (6)
(6)
и может применяться для проверки качества оценок, получаемых алгоритмом (5). Здесь z(
g) – переходная характеристика звена, параметрами которого являются элементы полученного вектора g; y – заданная переходная характеристика звена; q – весовые коэффициенты; N - максимальное число шагов процесса вычислений (измерений).Выражение (6) - одна из множества унимодальных функций рассогласования истинного и полученного в результате оцен-ки параметров выходного процесса иссле-дуемого звена на выбранном интервале наблюдения. Весовые коэффициенты q при-званы выделить наиболее информативный участок выходных процессов звена. Мини-мальное значение переменной h при вари-ации параметра регуляризации в области его определения позволит локализовать наиболее приемлемое значение e для конкретной задачи.
При поиске значения параметр регуля-ризации ввиду его малости удобно пред-ставлять в виде e
= (0.1b)10-a. Алгоритм поиска e в рассматриваемой постановке мо-жет быть основан на одном из методов по-иска экстремума функций нескольких пере-менных – градиентном, методе наискорей-шего спуска, методе возможных направле-ний, методе деления отрезка пополам и т.д.Рис. 1 и 2 иллюстрируют процедуру применения критерия (6) при выборе пара-метра регуляризации в задаче определения вектора
g для звена с передаточной функциейW(p) = (0.5p + 1)/(p3 + 2.5p2 + 4p + 1).
На рис. 1 приведены результаты выбора показателя степени a параметра регуляриза-ции в диапазоне a = 9..11 при b = 10. Из графика (см. рис.1) видно, что минимум критерия (6) достигается при a = 10 и равен h
= 5.58•10-6. Для найденного параметра регуляризации e = 10-10 с использованием алгоритма (5) был получен вектор g(10) с элементами (1.951, -1.376, 0.368, 0.0368, 0.0162, -0.0146). График, изображенный на рис.2, иллюстрирует высокую степень совпадения полученной z[g(10)] и истинной y1 переходных характеристик.Поиск константы b в диапазоне b = 5..7 при зафиксированном a = 10 позволил най-ти ее значение b = 6 и, тем самым, уточнить значение параметра регуляризации. При окончательном значении e
= 0.6·10-10 минимум функции (6) (h 6 = 4.1·10-6) по сравнению с полученной ранее величиной h 10 изменился незначительно. Расчеты проводились в среде MathCAD 7.0 Pro.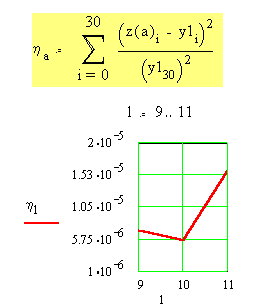
Рис.1. Результаты поиска константы a
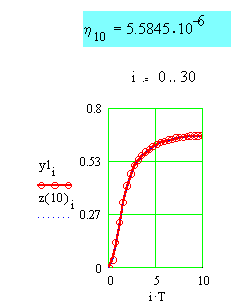
Рис. 2. Сопоставление переходных характеритик
Подход, аналогичный описанному, можно применить и к рекуррентной процедуре получения оценок искомого вектора
g. При этом в качестве параметра регуляризации можно рассматривать интенсивность R шума измерений. В этой постановке модель измеряемых сигналов будет иметь рекуррентную форму![]() g k+1 = g k ; y k+1
= f k g k+1
+ v k+1; (7)
g k+1 = g k ; y k+1
= f k g k+1
+ v k+1; (7)
![]() .
.
В обозначения (7) для большего удоб-ства записи введены незначительные изме-нения. В уравнении измерений добавлен аддитивный член v
k+1, имитирующий слу-чайную помеху типа дискретного белого шума с нулевым математическим ожидани-ем и интенсивностью R, выполняющей роль косвенного коэффициента регуляризации итеративного вычислительного процесса оценки вектора g вида [2]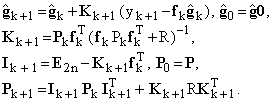
Здесь
Проведенный анализ возможностей повышения точности вычислений в задачах оценки рассматриваемого класса не явля-ется исчерпывающим, однако, дает направ-ление и варианты поиска.
Необходимо отметить, что процедуры поиска параметров регуляризации в рас-сматриваемой задаче требуют значи-тельных объемов вычислений. Поэтому при определении значений e вначале целесо-образно осуществлять грубый поиск этих параметров, чтобы при уточненном их определении предельно сократить число сопоставляемых вариантов.
Литература
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|