2Санкт-Петербургский государственный университет

Отсутствует однозначный выбор правил перехода от отдельных оценок к интегральной оценке. Даже существует мнение [1], что интегральная экологическая оценка геосистем может быть только качественной, чему способствует и не разработанность количественных оценочных параметров. Она во многом определяется опытом и интуицией исследователя. В тоже время отмечается [2], что оценка, безусловно, должна носить количественный характер.

Таким образом, мы сталкиваемся с решением вопросов однозначного определения компонентов вектора исходных характеристик, исследуемого объекта , однозначного задания функции , и определения вектора весовых коэффициентов . Для разрешения этих вопросов нами был использован подход, основанный на идее моделирования неопределенности выбора функций , и вектора весовых коэффициентов из классов функций и класса векторов соответственно.

Данные модели дефицита информации основаны на теории стохастических процессов и полей индуцируемых рандомизированными параметрами Математическая основа этой теории изложена в работе [3]. В рамках этой теории разработаны и программно реализованы в виде метода сводных показателей три блока алгоритмов.

Алгоритмы моделирования неопределенности выбора функций , и вектора весовых коэффициентов .

Самым сложным этапом в методе построения СП является оценка “весов” из-за обычно ограниченной информации об их точных числовых значениях. Как правило, исследователь обладает лишь нечисловой (ординальной) информацией, которая может быть описана системой равенств и неравенств и (или) неточной (интервальной) информацией, которая может быть представлена системой неравенств, определяющих интервалы изменения возможных значений весовых коэффициентов. Также наблюдаются случаи, когда значения некоторых весовых коэффициентов не входят в описанные системы равенств и неравенств. В таких случаях говорится о том, что информация является неполной. По аналогии с этим может использоваться порядковая информация относительно сравнительного предпочтения объектов исследования.

Выбор точности отсчетов h = 1/n весовых коэффициентов позволяет перейти от бесконечного набора всех возможных векторов к конечному набору (дискретному симплексу) всех возможных векторов с дискретными компонентами. Задание дополнительной экспертной информации позволяет перейти от набора всех возможных векторов с дискретными компонентами к набору всех допустимых векторов, удовлетворяющих требованиям экспертной информации.

Моделирование неопределенности выбора конкретного вектора 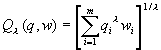из класса допустимых векторов осуществляется при помощи случайной m-мерной величины , равномерно распределенной на множестве . Полученные реализации случайного вектора позволяют отыскать набор всех допустимых функций свертки , получить усредненную оценку состояния объекта в виде математического ожидания , содержащего в неявном виде нечисловую, неточную и неполную информацию. Точность полученной оценки ` определяется стандартным отклонением случайной величины . Сравнение объектов проводится по величине математического ожидания их сводных показателей ` . Достоверность сравнения измеряется вероятностью по парного стохастического доминирования . В качестве свертки можно использовать синтезирующую функцию вида: , где параметр определяет конкретный вид интегрирующей функции. Для апробации метода сводных показателей нами использовался простейший вид сводного показателя – взвешенное арифметическое среднее : .

Метод сводных показателей был использован нами при создании многокритериальной классификации озерных систем, которая учитывала основные факторы, влияющие на потенциал водообмена [4].

Для решения этой задачи было выбрано 230 озерных систем, расположенных в зоне избыточного увлажнения, ограниченной территорией Кольского полуострова, Карелии, Северо-Западной и Нечерноземной частью Российской Федерации, стран Балтии и Беларуси. Эта территория является частью Северного озерного пояса Земли. На ней сосредоточено около 250 000 озер, в том числе более 30 000 с площадью зеркала, превышающей 1 км², в которых сосредоточено свыше 95 % водных ресурсов. Среди озер этого региона крупнейшие водоемы Европы – Ладожское, Онежское, Чудско-Псковское. Все озера сточные, а величина водообмена изменяется от нескольких сотен до 0,08 (Ладога).

Сводный показатель потенциала водообмена j-озерной системы определялся с учетом морфометрического , климатического , гидрологического и фактического потенциалов водообмена, оцененных в условиях современного климата и существующей антропогенной нагрузки. Поскольку значения сводного показателя существенно зависят от дополнительной информации I, задаваемой экспертом и учитывающей разную степень влияния отдельных показателей на сводный, в каждой из однородных групп исходных характеристик задавалось несколько вариантов расстановки приоритетов.

Другой практической сферой приложения метода сводных показателей стали исследования в области экологии человека. Нами была проведена оценка степени благоприятности природных условий для жизни людей[5]. В качестве объектов оценки были выбраны ландшафтные макрорегионы Северо-Запада России. Интегральная оценка проводилась по некоторым характерным показателям состояния. В качестве обучающей выборки был выбран ранжированный по принципу "лучше-хуже" ряд из 42 основных экологических типов геосистем [6]. Для обучающей выборки и для конкретных регионов были построены сводные показатели. В дальнейшем процедура оценивания сводилась к сопоставлению величин сводных показателей для конкретных регионов со значениями ранжированного ряда. В качестве экспертной информации при расчете весовых коэффициентов использовались положения Н.А.Солнцева [7] о том, что во взаимодействии "живой" и "мертвой" природы имеет место принцип неравнозначности в соответствии с положениями в генетическом ряде компонент.

1. Исаченко А.Г., Лавров С.Б., Морачевский В.Г. Методологические основы оценки эколого-географических состояний природной среды//Проблемы эколого-географической оценки состояния природной среды/Под ред. П.П.Арапов, Ю.П.Селиверстова. СПб. 1994.
2. Селиверстов Ю.П. Эколого-географическая оценка: понятия и проблемы//Проблемы эколого-географической оценки состояния природной среды/Под ред. П.П.Арапов, Ю.П.Селиверстова. СПб. 1994.
3. Хованов Н.В. Анализ и синтез показателей при информационном дефиците. СПб. 1996.
4. Догановский А.М., Мякишева Н.В. Многокритериальная классификация озерных систем в условиях неопределенности//Водные ресурсы северо-западного региона России/труды РГГМУ СПб. 1999. Вып.121.
5. Огурцов А.Н., Хованов Н.В. Многокритериальная оценка экологического состояния и устойчивости геосистем на основе метода сводных показателей. III. Оценка степени благоприятности природных условий макрорегионов северо-запада РФ для жизни людей//Вестник СПбГУ. Серия 7. Геология. География. 1997. Вып 2.
6. Исаченко А.Г. Оценка и картографирование экологического потенциала ландшафтов России//Изв. Всесоюз. Географич. Общ. 1991. Т. 123, вып. 6.
7. Солнцев Н.А. О взаимоотношениях "живой" и "мертвой" природы//Вестн. Моск. Ун-та.Сер. 5. География. 1960. №6.