 |
||
МОДЕЛИРОВАНИЕ СОСТОЯНИЯ СЕТИ СПУТНИКОВОЙ СВЯЗИ С НЕЧЕТКО ЗАДАННЫМИ ПАРАМЕТРАМИ
И. Б. Паращук, И. П. Бобрик, С.В. Дьяков
Военный университет связи
Abstract – The report is devoted to formulation of approach to the state modeling of a satellite communication network with inexplicitly prescribed parameters. The analytical model is based on use of the system of modified difference equations of the state for inexplicitly prescribed network parameters. The synthesis algorithm, allowing to transform inexplicit knowledge of a network parameters` state into quantitative values of the elements of transition probability matrices, is presented. Use of the model for the estimation of satellite communication network functioning efficiency permits to take into account both quantative and qualitative characteristics of an object and increase the degree of the validity of making decisions on network control.
В ряде работ, посвященных синтезу математических моделей для дискретных по состоянию, но непрерывных по времени процессов, в виде разрывных марковских последовательностей в форме стохастических дифференциалов [1,2] доказана принципиальная возможность введения унифицированных
моделей показателей качества (ПК) функционирования сети спутниковой связи (ССС) на основе управляемых цепей Маркова в форме разностных стохастических уравнений (УЦМ – РСУ). С точки зрения анализа эффективности функционирования ССС, данная модель, описывающая отклонения параметров ССС от требований, позволяет обеспечить совместное оценивание различных по физическому смыслу и по классу случайных процессов, позволяя получать интегральную (обобщенную) оценку эффективности функционирования сети. Для отдельно взятого ПК![]() ; (1)
; (1)
![]() ; (2)
; (2)
![]() ; (3)
; (3)
![]() , (4)
, (4)
где выражение (1) – уравнение состояния
процесса изменения отклонений ![]() на (k+1) шаге, в котором:
на (k+1) шаге, в котором: ![]() - матрица- строка возможных значений
ПК;
- матрица- строка возможных значений
ПК; ![]()
Предложенная модель состояния ССС на
основе УЦМ – РСУ позволяет получать значения ПК
функционирования сети на каждом ![]() -ом шаге, причем для любого ПК,
входящего в систему ПК, характеризующую сеть в
целом. Проблема заключается в том, что необходимо
идентифицировать элементы матриц переходных
вероятностей
-ом шаге, причем для любого ПК,
входящего в систему ПК, характеризующую сеть в
целом. Проблема заключается в том, что необходимо
идентифицировать элементы матриц переходных
вероятностей ![]() для
различных по классу ПК сети. Если решение данной
проблемы для количественно заданных параметров
сети не вызывает особых трудностей (элементы
матриц можно получить аналитически, опираясь на
интенсивность конкретного процесса и с
привлечением аппарата условных вероятностей), то
процесс идентификации элементов матриц
переходных вероятностей для описания параметров
ССС, заданных качественно (нечетко, с
привлечением лингвистической переменной)
сталкивается с определенными ограничениями.
для
различных по классу ПК сети. Если решение данной
проблемы для количественно заданных параметров
сети не вызывает особых трудностей (элементы
матриц можно получить аналитически, опираясь на
интенсивность конкретного процесса и с
привлечением аппарата условных вероятностей), то
процесс идентификации элементов матриц
переходных вероятностей для описания параметров
ССС, заданных качественно (нечетко, с
привлечением лингвистической переменной)
сталкивается с определенными ограничениями.
Суть возникающих трудностей при описании нечетко заданных параметров ССС заключается в том, что во-первых, в процессе идентификации нечетких исходных данных приходится опираться на мнения экспертов, а они нередко не совпадают, во-вторых, приведенная модель нуждается во введении конкретных количественных значений элементов матриц переходных вероятностей (МПВ), значит необходим математически корректный алгоритм приведения нечеткого множества к ближайшему четкому множеству, что в условиях, когда элементами множеств выступают вероятности, непросто, т.к. стык "вероятность – нечеткость" подразумевает необходимость введения метрики (эквивалента) нечеткого множества.
Таким образом, в рамках анализа эффективности функционирования ССС, очевиден выбор методики, называемой "параллельный анализ", когда ряд характеристик ССС можно оценить параметрически, традиционными методами, а ряд нечетко заданных параметров ССС, путем последовательных преобразований с использованием методов теории нечетких множеств, свести к возможности их относительно параметрической оценки, т.е. перейти от нечетко поставленной задачи к
параметрической. С точки зрения рассмотренной модели, возможно представление динамики изменения состояния ССС в виде набора систем разностных стохастических уравнений, причем описание количественно заданных параметров ССС будет составлять первый блок (систему) УЦМ – РСУ и будет выглядеть традиционно (выражения 1-4), тогда как динамика изменения состояния нечетко заданных параметров ССС может быть описана модифицированными разностными уравнениями и будет составлять второй блок (систему) УЦМ – РСУ. Формально изменится лишь ключевое выражение (2), характеризующее в нашем случае нечеткие знания операторов сети о вероятностях перехода параметров ССС из состояния в состояние:![]() , (5)
, (5)
где ![]() -
транспонированная матрица вероятностей
перехода нечетко заданных параметров ССС,
элементы которой получены с помощью экспертов.
Данная трактовка модели обязывает разработчика
(пользователя) ввести алгоритм
последовательного сведения нечетко заданных
характеристик (исходных данных) к виду,
обуславливающему возможность параметрической
оценки качества и эффективности
функционирования ССС.
-
транспонированная матрица вероятностей
перехода нечетко заданных параметров ССС,
элементы которой получены с помощью экспертов.
Данная трактовка модели обязывает разработчика
(пользователя) ввести алгоритм
последовательного сведения нечетко заданных
характеристик (исходных данных) к виду,
обуславливающему возможность параметрической
оценки качества и эффективности
функционирования ССС.
Для решения задачи объединения мнений экспертов о значениях элементов МПВ, нечетко заданных параметров ССС, предлагается воспользоваться одной из простейших операций над нечеткими множествами – операцией дизъюнктивного суммирования [3]. В этом случае дизъюнктивная сумма, например двух нечетких множеств (по количеству экспертов), определяется в терминах объединений и пересечений следующим образом:
![]() , (6)
, (6)
где ![]() - нечеткое
множество, характеризующее мнение первого
(второго) эксперта о вероятности перехода
нечетко заданного параметра ССС из состояния в
состояние
- нечеткое
множество, характеризующее мнение первого
(второго) эксперта о вероятности перехода
нечетко заданного параметра ССС из состояния в
состояние ![]()
![]() . Опираясь на алгоритм
вычисления дизъюнктивной суммы, рассмотрим
пример иллюстрирующий операции объединения и
пересечения двух нечетких множеств,
характеризующих степень уверенности экспертов в
количественных значениях элементов МПВ. Пусть
нечетко заданный параметр ССС может находиться в
трех состояниях: S1, S2, S3. Тогда МПВ имеет вид:
. Опираясь на алгоритм
вычисления дизъюнктивной суммы, рассмотрим
пример иллюстрирующий операции объединения и
пересечения двух нечетких множеств,
характеризующих степень уверенности экспертов в
количественных значениях элементов МПВ. Пусть
нечетко заданный параметр ССС может находиться в
трех состояниях: S1, S2, S3. Тогда МПВ имеет вид:
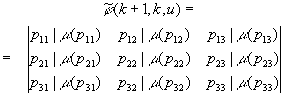 (7)
(7)
Для удобства формализованного описания модели и опроса экспертов, введем таблицу соответствий:
Таблица 1
|
0 |
0,1 |
0,2 |
… |
0,8 |
0,9 |
1 |
Элемент нечеткого множества |
|
|
|
… |
|
|
|
Данная таблица позволяет обратиться к
экспертам с вопросом: "с какой степенью
достоверности (уверенности) переход параметра
(ПК) из состояния i в состояние j произойдет с
вероятностью ![]() ?".
Тогда мнения двух экспертов о значениях
вероятностей перехода из первого состояния в
любое другое можно представить в виде двух
систем нечетких множеств, например:
?".
Тогда мнения двух экспертов о значениях
вероятностей перехода из первого состояния в
любое другое можно представить в виде двух
систем нечетких множеств, например:
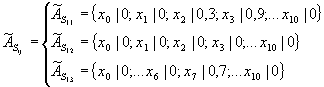 (8)
(8)
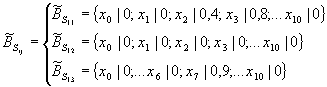 (9)
(9)
Для случая, когда определяется значение вероятности того, что параметр ССС на данном шаге функционирования сети был и останется в состоянии (i=1, j=1), т.е. S
11, определим дополнения нечетких множеств![]()
![]()
В соответствии с алгоритмом дизъюнктивного суммирования [3] для рассмотренных исходных данных получим:
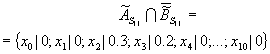
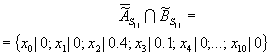
Мнения экспертов о количественных значениях вероятности того, что параметр ССС был и останется в состоянии S
11 окончательно определяется по закону дизъюнктивного суммирования нечетких множеств: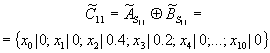
Аналогично определяются нечеткие множества, характеризующие мнения экспертов о количественных значениях вероятностей перехода из первого во второе и третье состояние (S
12 и S13):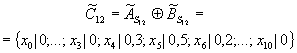
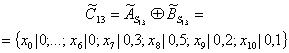
Для предварительного выбора
количественных значений элементов МПВ ![]() предлагается
воспользоваться функцией:
предлагается
воспользоваться функцией:
![]() , (10)
, (10)
характеризующей максимальную функцию
принадлежности (степень уверенности)
интегрированного мнения экспертов по каждому из
нечетких множеств ![]() ,
описывающих элементы МПВ. В соответствии с
выражением (10) и таблицей 1, получаем
предварительные количественные значения
вероятностей перехода для первой строки МПВ (7):
,
описывающих элементы МПВ. В соответствии с
выражением (10) и таблицей 1, получаем
предварительные количественные значения
вероятностей перехода для первой строки МПВ (7):
![]()
![]() .
.
Однако, обязательным условием идентификации элементов МПВ является условие нормировки, т.е. суммарное значение вероятностей в любой строке МПВ не должно превышать 1. Условие нормировки реализуется с помощью выражения:
![]() , (11)
, (11)
где ![]() - сумма
полученных предварительных значений
вероятностей перехода всех элементов данной
строки МПВ. Окончательный результат:
- сумма
полученных предварительных значений
вероятностей перехода всех элементов данной
строки МПВ. Окончательный результат:![]()
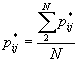 , (12)
, (12)
где N – количество одинаковых значений
функции принадлежности ![]() для нечеткого множества
для нечеткого множества ![]() . Например, для произвольно взятого
случая:
. Например, для произвольно взятого
случая:
![]() ,
,
используя выражение (12) получим: ![]()
Если функции принадлежности ![]() для различных
для различных ![]() совпадают, воспользуемся
положением, оговоренным в работе [4] и
доказывающим возможность получения степеней
принадлежности, опираясь на вероятность выбора
элемента. Например, пусть в двух нечетких
множествах из трех функций принадлежности
совпали и результатом решения уравнения (10)
явились предварительные значения:
совпадают, воспользуемся
положением, оговоренным в работе [4] и
доказывающим возможность получения степеней
принадлежности, опираясь на вероятность выбора
элемента. Например, пусть в двух нечетких
множествах из трех функций принадлежности
совпали и результатом решения уравнения (10)
явились предварительные значения:
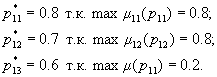
Предлагается воспользоваться модифицированным выражением для выполнения условий нормировки:
![]() . (13)
. (13)
В этом случае: ![]()
![]() , что
значительно больше соответствует физическому
смыслу вероятностей
, что
значительно больше соответствует физическому
смыслу вероятностей ![]() ,
чем, если бы воспользовались рассмотренным ранее
выражением (11).
,
чем, если бы воспользовались рассмотренным ранее
выражением (11).
Таким образом, сформулирован подход к моделированию состояния ССС с нечетко заданными параметрами ориентированный на "параллельный анализ" эффективности функционирования сети и основанный на использовании: систем разностных стохастических уравнений для количественно заданных характеристик ССС; систем модифицированных разностных уравнений состояния, в которых нечеткие знания о поведении
некоторых параметров сети путем математически корректных последовательных преобразований, трансформируются в количественные значения элементов МПВ – одной из основных составляющих модели. Предложенный алгоритм синтеза аналитической модели состояния ССС позволяет наиболее полно учесть весь спектр исходных данных (как на количественном, так и на качественном уровне) в интересах оценки эффективности функционирования сети, что в конечном итоге повышает степень обоснованности принимаемых решений по управлению структурой, параметрами и режимами работы сетей спутниковой связи.Литература
1.Терентьев В.М. Автоматизированные системы управления сетями многоканальной радиосвязи. –Л.: ВАС,1986.-116с.
2.Терентьев В.М., Паращук И.Б. Теоретические основы управления сетями многоканальной радиосвязи. – СПб.: ВАС,1995.–195с.
3. Кофман А. Введение в теорию нечетких множеств: Пер. с франц. – М.: Радио и связь,1982.-432с.
4. Нечеткие множества и теория возможностей. Последние достижения: Пер. с англ./ Под ред. Р.Р.Ягера.- М.: Радио и связь. 1986.-408с.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|