 |
||
НОВЫЕ МЕТОДЫ ФОРМИРОВАНИЯ ПРИЗНАКОВ РАСПОЗНАВАНИЯ ОБРАЗОВ С ПОЗИЦИЙ СТОХАСТИЧЕСКОЙ ГЕОМЕТРИИ
Н.Г. Федотов, Л.А. Шульга
Пензенский государственный университет
Abstract – Проанализировано применение методов стохастической геометрии в распознавании образов. Рассуждения проводились на базе введенного авторами Тгасе-преобразования исходных изображений в изображения на листе Мебиуса. Предложен новый подход к формированию признаков распознавания
, не зависящих от движений изображений, а также от их линейных деформаций. Отличительной чертой группы рассматриваемых признаков является представление каждого из них в виде последовательной композиции трех функционалов.Введение. В распознавании образов традиционно выделяют формирование признаков и решающую процедуру. В кибернетической литературе исторически сложилось так, что подавляющее большинство работ по распознаванию образов посвящено решающим правилам и практически нет работ по формированию признаков. По общепринятому мнению это объясняется тем, что процесс формирования признаков является эмпирическим и зависит от интуиции проектировщика распознающей системы.
Подход с позиций стохастической геометрии, развитый в [1], позволяет восполнить этот пробел и, наряду с конструктивной теорией признаков, дать практические методы генерации большого числа новых признаков распознавания изображений. Столь мощное смещение акцента с решающих правил на новые признаки распознавания сближает данный подход с нейрокомпьютингом.
В работе [1] предложено в качестве признаков распознавания изображений использовать вероятности геометрических событий, под которыми понимают результат взаимодействия геометрических объектов: пересечения, покрытия и т. п. Роль геометрических объектов выполняют, с одной стороны, сложные траектории сканирования со случайными параметрами (отрезки, линии, кривые, фигуры и т. п.), с другой — фрагменты распознаваемого изображения. Рассматривается структура подобных распознающих систем, примеры конкретных технических реализаций. Рассмотрены также возможные расширения базисного метода распознавания, основанного на стохастической геометрии. Одно из расширений связано с усложнением наблюдений случайного события — пересечения линии развертки с изображением, т. е
. с применением более сложных признаков распознавания.В статье представлены начала новой теории формирования признаков распознавания, не зависящих от движений изображений, а также от аффинных преобразований. Отличительной чертой группы рассматриваемых признаков является представление каждого из них в виде последовательной композиции трех функционалов.
Рассмотрим входную сетчатку
распознающего устройства, под которой будем
понимать сканируемую часть плоскости
изображения. В этой части плоскости
располагается некоторое изображение, тогда как
оставшаяся часть плоскости — фоновая. Таким
образом, изображение финитно. Рассмотрим
случайную прямую ![]() ,
которая может пересекать изображение.
Предположим, что пересечение прямой
,
которая может пересекать изображение.
Предположим, что пересечение прямой ![]() и изображения позволяет нам
вычислить некоторое число
и изображения позволяет нам
вычислить некоторое число ![]()
Математическая сторона рассмотренной
процедуры интенсивно исследовалась в
стохастической геометрии. Было выяснено, что при
некоторых условиях характеристика ![]() может иметь явный геометрический
смысл. Для нас важно, что, легко реализуясь в
устройствах, эта идея может служить исходной
точкой для получения новых признаков
распознавания образов как в теоретическом
анализе, так и в практической сфере.
может иметь явный геометрический
смысл. Для нас важно, что, легко реализуясь в
устройствах, эта идея может служить исходной
точкой для получения новых признаков
распознавания образов как в теоретическом
анализе, так и в практической сфере.
В [1] приводятся формулы, на основе которых строятся критерии распознавания. Рассматриваются только бинарные изображения (черные фигуры на белом фоне).
1. Рассмотрим изображение в виде
кусочно-дифференцируемой кривой, которая может
быть границей фигуры. Пусть ![]()
2. Рассмотрим изображение в виде
выпуклой фигуры. Это может быть выпуклая
оболочка некоторой другой фигуры. Пусть ![]()
Тгасе-преобразование. Приведенные выше формулы и их многочисленные аналоги имеют для распознавания образов следующие недостатки: 1) число этих формул ограничено, поскольку ясно выраженных геометрических характеристик не так много, а признаков требуются тысячи и более;
2) формулы применимы только для бинарных изображений. К достоинствам следует отнести возможности параллельных вычислений (одновременно обрабатывается несколько прямых сразу) и стохастической реализации, последнее позволяет оборвать процесс при достижении нужной точности, кроме того, вычисленные признаки не зависят от движений объектов. Известно, что обычно признаки сильно зависят от поворота и сдвига объекта, в то время как во многих задачах распознавания поворот и сдвиг объектов совершенно неинформативны.В данной работе мы предлагаем обобщение приведенного выше подхода с целью преодоления его недостатков и с сохранением достоинств, причем это обобщение в некотором смысле полное.
Обозначим буквой ![]() финитное изображение. Если дана прямая
финитное изображение. Если дана прямая ![]() , то число
, то число ![]() , характеризующее взаимное
расположение прямой
, характеризующее взаимное
расположение прямой ![]() и
изображения, будем вычислять согласно
некоторому правилу
и
изображения, будем вычислять согласно
некоторому правилу
Аналогично, как и в стохастической
геометрии, определена случайная величина ![]() , распределение которой не
зависит от сдвигов и поворотов изображения.
Поэтому числовые характеристики этой случайной
величины опять могут служить признаками
изображений, которые определяются специальными
техническими устройствами и системами.
Недостаток нового семейства признаков —
первоначальное отсутствие ясного
геометрического смысла, и заранее не известна их
различающая сила. Однако для распознавания
образов это не так важно, ибо решающей все-таки
является экспериментальная проверка.
, распределение которой не
зависит от сдвигов и поворотов изображения.
Поэтому числовые характеристики этой случайной
величины опять могут служить признаками
изображений, которые определяются специальными
техническими устройствами и системами.
Недостаток нового семейства признаков —
первоначальное отсутствие ясного
геометрического смысла, и заранее не известна их
различающая сила. Однако для распознавания
образов это не так важно, ибо решающей все-таки
является экспериментальная проверка.
Отметим еще одно свойство вполне
инвариантного функционала ![]() (Тгасе): он не обязательно определяется
лишь сечением прямой изображения. Для его
вычисления может быть привлечена также и другая
информация, например, свойства окрестности этого
сечения.
(Тгасе): он не обязательно определяется
лишь сечением прямой изображения. Для его
вычисления может быть привлечена также и другая
информация, например, свойства окрестности этого
сечения.
Чтобы понять, что предложенное
обобщение в некотором смысле исчерпывает все его
возможности, изложим теорию
Тгасе-преобразований (или Тг-преобразований).
Прямая ![]() , если введены
полярные координаты на плоскости,
характеризуется расстоянием
, если введены
полярные координаты на плоскости,
характеризуется расстоянием ![]() от начала координат до нее и углом
от начала координат до нее и углом ![]() (с точностью до 2
(с точностью до 2![]()
![]() ,
, ![]() ,
,
где ![]()
![]() .
.
Таким образом, множество всех
направленных прямых, пересекающих круг радиусом ![]() с центром в начале
координат (“сетчатку”), однозначно
параметризуется множеством
с центром в начале
координат (“сетчатку”), однозначно
параметризуется множеством
![]()
при условии, что параметры ![]() и
и ![]() задают
одну прямую. Видно, что множество прямых на
сетчатке есть в топологическом смысле не что
иное, как лист Мебиуса [2]. Множество чисел
задают
одну прямую. Видно, что множество прямых на
сетчатке есть в топологическом смысле не что
иное, как лист Мебиуса [2]. Множество чисел ![]()
Будем считать дополнительно, что если
прямая ![]() не пересекает
изображения, то
не пересекает
изображения, то ![]() есть
заданное число (например, 0), или другой
фиксированный элемент, если функционал
есть
заданное число (например, 0), или другой
фиксированный элемент, если функционал ![]() нечисловой. В этом случае
первоначальному изображению
нечисловой. В этом случае
первоначальному изображению ![]() соответствует Tr (
соответствует Tr (![]()
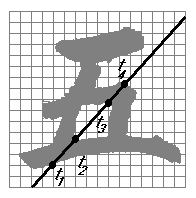
Рис. 1.а
Рис. 1.а объясняет вычисление Trace -
преобразования. Здесь показано получение
бинарной функции ![]() действительной
переменной при сканировании прямой
действительной
переменной при сканировании прямой ![]() . Функция
. Функция ![]() равна
1 в интервалах
равна
1 в интервалах ![]() и
и ![]() , и принимает значение 0
для других. Рассмотрим функционал
, и принимает значение 0
для других. Рассмотрим функционал

Рис. 1.б
Заметим, что известное преобразование Радона [3 ] может рассматриваться как пример Тг-преобразования.
Кратко остановимся на том, как
меняется изображение ![]() при
сдвигах и вращениях исходного изображения
при
сдвигах и вращениях исходного изображения ![]()
На рис. 2 представлены изображение Японского иероглифа и результат его Тг-преобразования — Тг-трансформанта, на рис. 3,4 — изображение этого же иероглифа при сдвигах и соответствующие Тг-трансформанты, на рис. 5 — изображение иероглифа, претерпевшее масштабное преобразование, и соответствующая ему расширенная Тг-трансформанта, на рис. 6 — повернутое изображение данного иероглифа

 Рис.2
Рис.2

 Рис.3
Рис.3

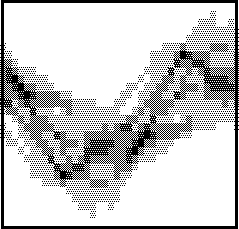 Рис.4
Рис.4
и ее Тг-трансформанта, сдвинутая по горизонтальной оси.
Обычная евклидова мера ![]() листа Мебиуса инвариантна к
указанным преобразованиям, поэтому плотность
распределения всякой функции, заданной на листе
Мебиуса, в данном случае функции изображения Tr(
листа Мебиуса инвариантна к
указанным преобразованиям, поэтому плотность
распределения всякой функции, заданной на листе
Мебиуса, в данном случае функции изображения Tr(
 Р
Р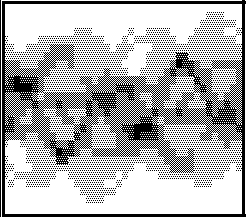 ис.5
ис.5

 Рис.6
Рис.6
Триплексные признаки. Рассмотрим формирование триплексных признаков, представляющих
последовательную композицию трех функционалов:
![]() .
.
Каждый функционал (![]()
Для распознавания ![]() объектов требуется порядка
объектов требуется порядка ![]() признаков, следовательно, мы
получаем возможность распознавать очень большое
число изображений, например идеограмм.
признаков, следовательно, мы
получаем возможность распознавать очень большое
число изображений, например идеограмм.
Функционал ![]()
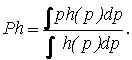
Результат применения функционала ![]() ("Norm") Trace - матрицы
(рис.1.б) - 2
("Norm") Trace - матрицы
(рис.1.б) - 2![]() -
периодическая кривая, показанная на рис.7
-
периодическая кривая, показанная на рис.7
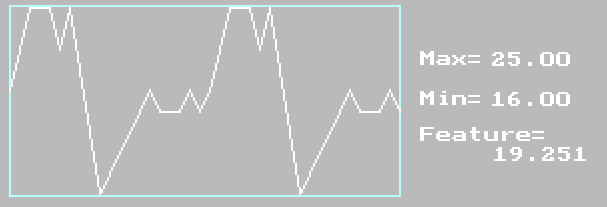
Рис. 7
Следующий этап должен выполнить
преобразования на кривой с помощью ![]() функционала, который мы называем
круговым. Функционал "Log" был использован в
качестве варианта кругового функционала
функционала, который мы называем
круговым. Функционал "Log" был использован в
качестве варианта кругового функционала ![]()
![]()
Вывод. Описанная теория триплетных признаков дает возможно генерировать большое число, фактически тысячи, которые доказывает лишь ценность для задач распознавания образов с множественной структурой классов, скажем, для задачи распознавания иероглифов. Полученные признаки можно обобщить и для распознавания полутоновых и цветных изображений.
Рассмотренные триплексные признаки распознавания могут быть вычислены в высшей степени параллельном процессе. Подобно признакам, формируемым нейронными сетями, данные признаки не имеют наперед заданного смысла, их отбор осуществляется в ходе машинного эксперимента, принимая во внимание исключительно лишь их полезность для классификации.
Литература
1. Федотов Н. Г. Методы стохастической геометрии и распознавании образов. М.: Радио и связь, 1990.
2. Масси У., Столлингс Дж. Алгебраическая топология. Введение. М.: Мир, 1977.
3. Хелгасон С. Преобразование Радона. М.: Мир, 1983.
4. Kadyrov A.A and Fedotov N.G. Triple Features Pattern Recognition and Image Analysis, vol. N4, 1995.
5. Fedotov N.G. and Tuzilov I.V. Neural Computing Procedures to Make Decisions in systems with Pattern Recognition Feature Automatic Generations. Proceedings International Conference on Soft Computing and Meassurements (Russia, S.-Petersburg, 22-26 June 1998), vol.1, S.-Petersburg, 1998, pp.337-340.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|