Хорошо известны трудности применения формулы Байеса в задачах медицинской диагностики. Одна из них связана с оценкой вероятности P(x/D_k ), где x – n-мерный вектор лабораторных и инструментальных признаков, а D_k (k = 1, 2, …, m) – клинические состояния. Обычно эта трудность преодолевается предположением о независимости признаков и применением формулы Байеса для каждого признака отдельно. Получаемые апостериорные вероятности затем складываются и решение принимается либо по средней арифметической этих вероятностей либо по их сумме [1].

Другая принципиальная трудность обусловлена необходимостью знать априорные вероятности клинических состояний D_k.

Ниже излагается методология введения вероятностной меры в пространстве клинико-лабораторных признаков и алгоритм, опирающийся на формулу Байеса, в котором отсутствие знания об априорных вероятностях не существенно, а необходимая оценка P(x/D_k) по эмпирическим данным обеспечивается наилучшим образом.

Пусть вектор х = {x¹, x² ,…, xⁿ} – набор из n значений количественных и качественных признаков, элемент n-мерного пространства. Векторы x₁, x₂, …, x_N содержат информацию о состоянии N пациентов (или информацию о состоянии одного пациента в N моментов времени). Множество векторов {x}={x₁, x₂, …, x_N}, обусловленных клинической ситуацией D, будем называть образом в пространстве признаков и обозначать {х}_D.

Пусть Q(x_i), i=1, 2, …, n – диапазон допустимых значений признака х_i, совместимых с жизнью организма (для перечислимых признаков это не диапазон, а дискретное множество).

С точки зрения системного подхода, {x}_D = {x₁, x₂, …, x_N} в теоретическом, идеальном случае может быть представлено как подмножество прямого произведения Q(x₁) ґ Q(x₂) ґ … ґ Q(x_n) [4 ].

Если вместо оценки средних и коэффициентов корреляции (в случае медицинских данных приводящих к большим потерям информации) использовать вероятностные меры для всех Q(х_i) и для всех бинарных отношений Q(x_i)ґ Q(x_j), то принципиально расширяются возможности описания информации по сравнению с многомерной нормальной моделью.

Другими словами, предполагается, что основная информация об {x}_D содержится в подмножестве S множества одномерных и двумерных элементов. Т.е. мы имеем отображение

{x}_{D ®} S (*)

1. основную информацию о n-мерном многообразии любой сложной структуры свести к информации, заключенной в одномерных и двумерных объектах, для которых становится реальным введение вероятностной меры;
2. использовать адекватные методы анализа частот при анализе разнотипных клинико-лабораторных данных (числа, перечисления и др.).

Введение вероятностной меры в n-мерном пространстве досталось ценой значительного увеличения числа признаков, так как вместо одного n-мерного образа анализируются n одномерных и n(n – 1)/2 двумерных множеств. Но уже само введение вероятностной меры позволяет эффективно оценить значимость информации, заключенной в элементах множества (*), а затем значительно сократить их число [2,3]. Поэтому, на самом деле, наиболее важную информацию о клинической ситуации удается экономно представить в виде небольшого числа частотных распределений – интервальных и бинарных (матричных) структур.

Пусть x = {х¹, х², …, хⁿ} – описание одного пациента в n–мерном пространстве клинико-лабораторных признаков – точка в n-мерном абстрактном пространстве; {x}_D1, {x}_D2,, …, {x}_Dm – множества векторов – образов, индуцируемых клиническими ситуациями D_1,, D₂,, ..., D_m, которые отражают цели, стоящие перед исследователем.

Введем разбиение d диапазона [a, b] на небольшое число (не больше четырех) отдельных диапазонов, длины которых заранее не предопределены. Обозначим через р_s (x/D_k) частоту попадания значения признака х (х – любое значение признака х) в s-й диапазон.

Для двух референтных условий D_k и D_l в качестве наилучшего разбиения диапазона [а,b] выбирается разбиение, обеспечивающее функционалу Кульбака J(D_k:D_l, x) [2] значение, близкое к наибольшему, т.е такое разбиение d , при котором можно наилучшим образом использовать дифференциально-диагностические возможности признака х для пары референтных условий D _k и D _l.

Интервалы, образующие разбиение, вместе с вероятностями появления значения признака в каждом из этих интервалов будем называть интервальной структурой.

Для двух признаков x_i и x_{j ,} зная разбиения d ₁ и d ₂ для каждого из них, естественным образом строятся оценки р (xⁱ,x^j /D_k) – частоты попадания пары значений признаков хⁱ и х^j в соответствующие прямоугольники. Множество прямоугольников вместе с оценками p (xⁱ,x^j /D_k) предлагается называть бинарной (матричной) структурой, а соответствующую пару признаков – двумерным признаком.

Интервальные и бинарные структуры – удобные инструменты формализации медико-биологических знаний и источник информации для эффективных диагностических алгоритмов, использующих статистические стратегии распознавания образов.

При построении интервальных и бинарных структур появляется возможность отбирать такие одномерные и двумерные признаки, которые содержат информацию для решения дифференциально-диагностических задач – информативные признаки. На основании величины функционала Кульбака и числа наблюдений, участвующих в формировании интервальных и бинарных структур, признаки упорядочиваются по возрастанию уровня значимости различий P [2, 3]. Те из них, для которых P > 0.1, исключаются из описания информационного образа клинической ситуации. Так, при n = 100 формируется 5050 одномерных и двумерных признаков. Если решается сложная дифференциально-диагностическая задача, в результате отбора обычно остается не более 50 информативных признаков.

При разработке решающего правила нет необходимости использовать все информативные признаки. Всегда существуют подмножества информационно-ценных признаков (вообще говоря, различные для разных стратегий распознавания), которые обеспечивают более высокие результаты. Алгоритм поиска таких подмножеств будет рассмотрен в п.5.

4. Многошаговый байесовский процесс

Пусть х₁, х₂, …, х_n – упорядоченные по убыванию информативности признаки, как одномерные, так и двумерные, отобранные для решения интересующей нас задачи. Для простоты изложения ограничимся тремя клиническими ситуациями D₁, D₂, D₃.

1. На первом шаге формула Байеса применяется для наиболее информативного признака х₁ и _.гипотезы считаются равновероятными.

2) На втором шаге полученные вероятности используются как априорные для признака x₂.

3) На третьем шаге для признака х₃ в качестве априорных вероятностей используются полученные на втором шаге:

5. Отбор подмножества информационно-ценных признаков

Второй вариант – более трудоемкий – отличается тем, что на каждом шаге при выборе очередного признака просматриваются все оставшиеся признаки, а не только те, которые на предыдущем шаге улучшали результат. Этот вариант поиска информационно-ценных признаков приводит к подмножеству, дающему лучшие результаты. Число информационно-ценных признаков значительно меньше числа информативных.

6. Применение

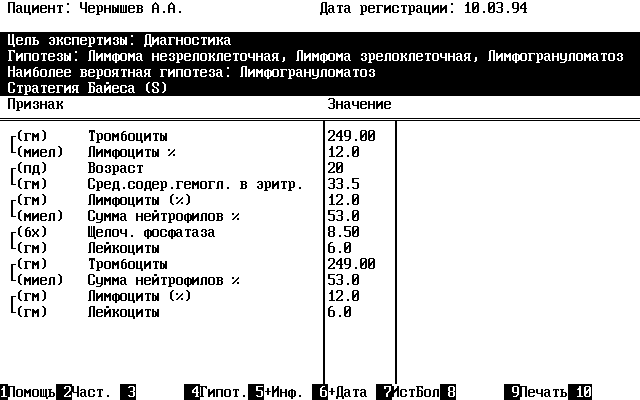
Последовательная байесовская стратегия, наряду со стратегиями Неймана-Пирсона, Вальда, классической байесовской процедурой и др., используется при разработке решающих правил в программном комплексе ОМИС в различных областях медицины [5]. В качестве иллюстрации ниже приведен фрагмент экрана экспертного модуля с вероятностями гипотез на заключительном шаге последовательного байесовского алгоритма при распознавании лимфогранулематоза, зрелоклеточной и незрелоклеточной лимфом, у одного из пациентов без гистологической и цитологической информации.

[1] Ластед Л. Введение в проблему принятия решений в медицине – М. Мир, 1971.

[2] Кульбак С. Теория информация и статистика – М. Наука, 1967.

[3] Колмогоров А.Н. Предисловие редактора перевода книги [2].

[4] Клир Дж. Системология. Автоматизация решения системных задач – М. Радио и связь, 1990.

[5] Генкин А.А. Новая информационная технология анализа медицинских данных – СПб. Политехника, 1999.