В. В. Губарев, В. А. Третьяков

Новосибирский Государственный Технический университет

В науке и практике модели реальных объектов часто строят по экспериментальным данным. Такой подход к построению моделей называется идентификацией. В этом случае для построения модели исследователь использует информацию о входных воздействиях на объект и реакциях этого объекта на данные входные воздействия.

Под объектами типа Гаммерштейна – Винера принято понимать объекты, состоящие из последовательно соединённых статических нелинейных объектов (СНЭ) и динамических линейных элементов (ДЛЭ) и имеющие одну из структур, изображённых на рис. 1.

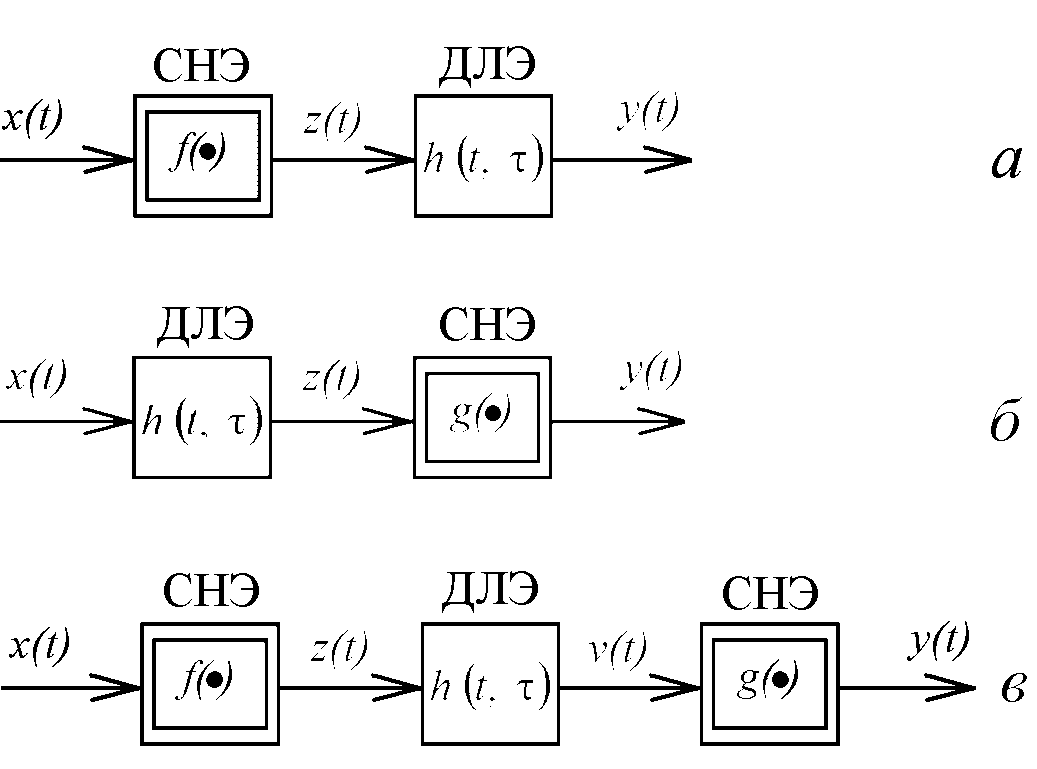
Рис. 1. Структурные схемы последовательного соединения нелинейного и линейного звеньев:

а) объект Гаммерштейна; б) объект Винера;

в) объект Гаммерштейна – Винера

Основная сложность в построении моделей таких объектов заключается в том, что внутренние сигналы и являются недоступными для измерения.

Одним из основных требований к моделям является их адекватность, то есть соответствие объекту, целям, задачам и условиям моделирования, а так же исходным данным для моделирования [1].

В настоящей работе вводятся новые модели объектов типа Гаммерштейна - Винера, полученные на основе конкорреляционных методов идентификации [2, 4, 6], оперирующих классом нетрадиционных характеристик связи случайных процессов конкорреляционных функций, описывается подход для исследования адекватности введённых моделей, и приводятся некоторые результаты этих исследований.

Кроме того, полуконкорреляционные функции (ПККФ), это:

Для объектов Гаммерштейна, предложенные нами модели, изображены на рис. 2,

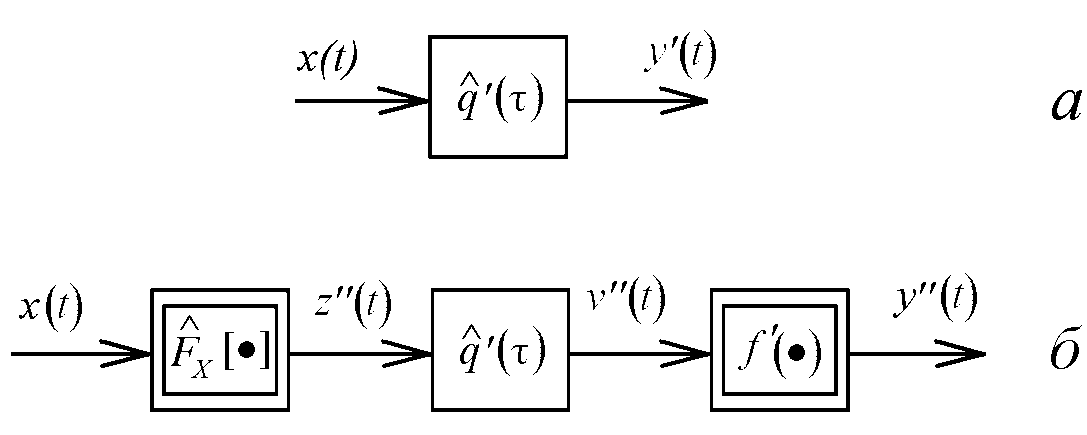
Рис. 2. Модели объектов Гаммерштейна

Для объектов Винера были предложены модели, изображённые на рис. 3,

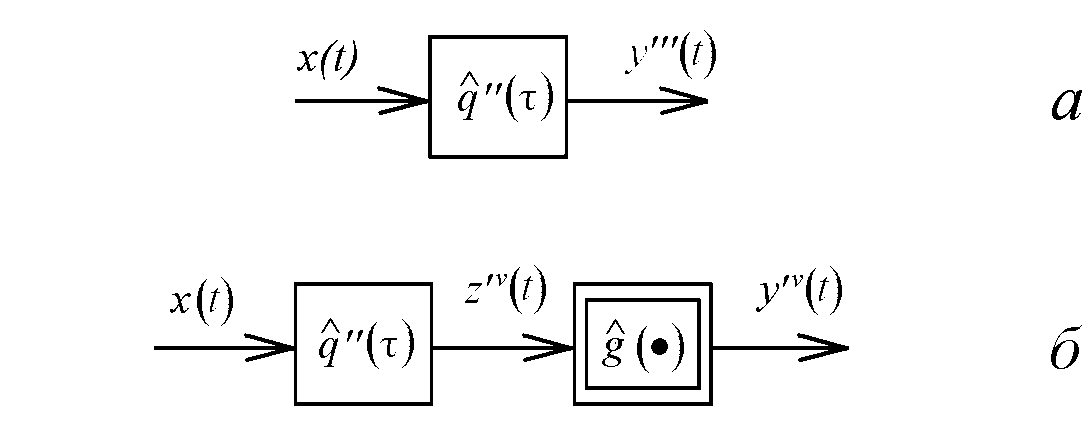
Рис. 3. Модели объектов Винера

где - оценка полуконимпульсной характеристики, получаемая на основе соотношения

Для объектов Гаммерштейна - Винера были предложены модели, изображённые на рис. 4,

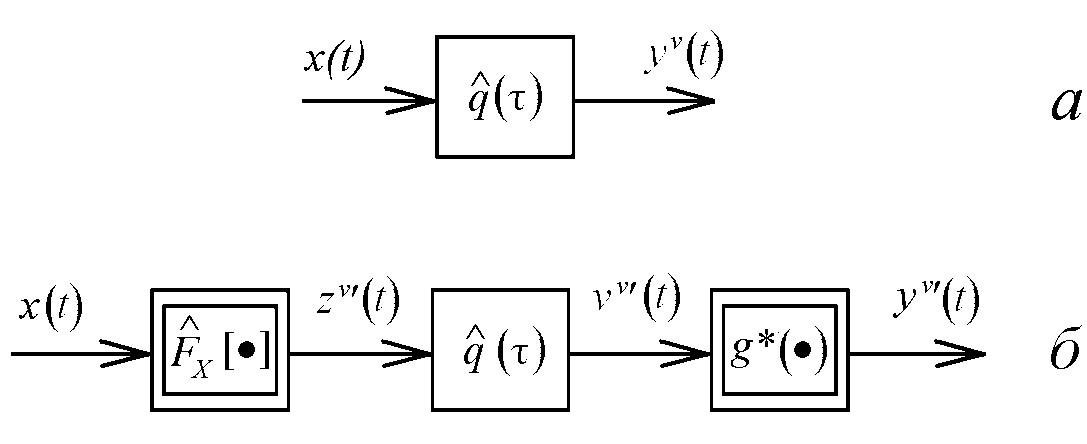
Рис. 4. Модели объектов Гаммерштейна – Винера

Для введённых нами моделей с помощью машинного экспериментирования необходимо было оценить, насколько они адекватны тем объектам, для которых они были построены. Для этого была создана программная экспериментальная система. Проверка адекватности моделей на этой экспериментальной системе проводилась по методу образцового объекта, путём сопоставления сигналов, КФ и ККФ на выходе объекта с сигналами, КФ и ККФ на выходах моделей при одинаковых входных воздействиях.

Созданная экспериментальная система позволяет решать следующие задачи:

1. Оценка адекватности введённых моделей по отношению к самим входным и выходным сигналам.

2. Оценка адекватности введённых моделей по отношению к характеристикам входных и выходных сигналов (в частности, по отношению к КФ, ККФ, СПМ, КПМ, законам распределения ЗР.

Машинные эксперименты с моделью, изображённой на рис. 3, б показали адекватность этой модели по отношению к конкорреляционным характеристикам (ККФ, КПМ) на выходе. То есть, при подаче на вход объекта и модели идентичных сигналов, ККФ и КПМ выходных сигналов совпадают до вычислительных и статистических погрешностей.

Машинные эксперименты с моделями, изображёнными на рис. 2, б; рис. 3, б; рис. 4, б показали в адекватность этих моделей по отношению к самим сигналам на выходе и их КФ и СПМ.

С помощью созданной экспериментальной системы планируется продолжить исследования поведения введённых в этой работе моделей.

Работа выполняется в рамках гранта по информатике и кибернетике.