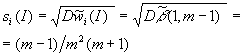БАЙЕСОВСКАЯ МОДЕЛЬ ОБРАБОТКИ
НЕЧИСЛОВОЙ, НЕТОЧНОЙ И НЕПОЛНОЙ ИНФОРМАЦИИ О
ВЕСОВЫХ КОЭФФИЦИЕНТАХ
В.В. Корников, И.А. Серегин, Н.В. Хованов
Санкт-Петербургский государственный
университет
Abstract – A method for non-numeric,
non-exact and non-complete information (nnn-information) treatment is proposed. The
method is based on Thomas Bayes' conception, which may be named "randomization of
uncertainty". In accordance with this conception an uncertain choice of a weight-vector
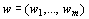 ,
, 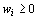 ,
, 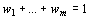 , from a fixed set
, from a fixed set 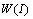 is modeled by a random choice which leads to a
random weight-vector
is modeled by a random choice which leads to a
random weight-vector 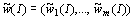 distributed on the
set
distributed on the
set 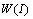 . The set
. The set 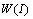 being determined by a nnn-information
being determined by a nnn-information 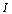 , the vector
, the vector 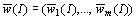 , where
, where 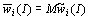 ,
, 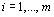 , are mathematical expectations of the
corresponding randomized weight-coefficients, may be treated as a "numeric
image of nnn-information
, are mathematical expectations of the
corresponding randomized weight-coefficients, may be treated as a "numeric
image of nnn-information 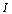 ". Some
applications of these models and conceptions to decision-making under uncertainty are
demonstrated.
". Some
applications of these models and conceptions to decision-making under uncertainty are
demonstrated.
Во многих задачах теории принятия
решений при неопределенности фигурируют так
называемые весовые коэффициенты,
представляющие собой неотрицательные величины
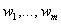 ,
связанные нормирующим соотношением
,
связанные нормирующим соотношением 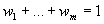 . Иными
словами, вектор весовых коэффициентов
("весовой вектор", "вектор весов")
. Иными
словами, вектор весовых коэффициентов
("весовой вектор", "вектор весов") 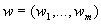 представляет собой точку
представляет собой точку 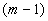 -мерного симплекса
-мерного симплекса 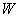 , лежащего
в
, лежащего
в 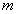 -мерном
евклидовом пространстве
-мерном
евклидовом пространстве 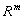 .
.
Мы будем ориентироваться на следующие
три основные задачи теории принятия решений,
связанные с применением весовых коэффициентов.
- Задача построения сводного показателя
качества
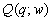 , определяемого каким-либо
обобщенным средним
, определяемого каким-либо
обобщенным средним
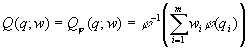 ,
,
где
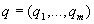 - вектор отдельных
показателей качества,
- вектор отдельных
показателей качества, 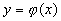 - непрерывная строго
возрастающая функция, а
- непрерывная строго
возрастающая функция, а 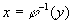 - функция, обратная к
функции
- функция, обратная к
функции 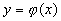 [1]. В этом случае весовой коэффициент
[1]. В этом случае весовой коэффициент 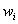 есть мера
относительной значимости отдельного показателя
есть мера
относительной значимости отдельного показателя 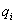 для
сводной оценки
для
сводной оценки 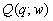 .
Задача распределения единичного ресур-
.
Задача распределения единичного ресур-
са по
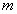 позициям с оценкой варианта
распределения по формуле
позициям с оценкой варианта
распределения по формуле
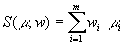 ,
,
где
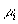 - эффективность
единицы ресурса, распределенного на
- эффективность
единицы ресурса, распределенного на 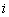 -ю позицию.
В этом случае весовой коэффициент
-ю позицию.
В этом случае весовой коэффициент 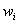 указывает долю единичного ресурса,
распределенного на
указывает долю единичного ресурса,
распределенного на 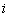 -ю позицию. В частности,
-ю позицию. В частности, 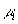 можно
интерпретировать как ожидаемую доходность
денежной единицы, вложенной в
можно
интерпретировать как ожидаемую доходность
денежной единицы, вложенной в 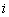 -й финансовый
инструмент, а
-й финансовый
инструмент, а 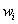 - как долю общего объема инвестиций,
приходящуюся на этот финансовый инструмент.
Тогда
- как долю общего объема инвестиций,
приходящуюся на этот финансовый инструмент.
Тогда 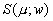 есть ожидаемый доход всего
инвестиционного портфеля [2].
Задача определения вероятности некоторого
события
есть ожидаемый доход всего
инвестиционного портфеля [2].
Задача определения вероятности некоторого
события 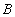 по известной формуле полной
вероятности
по известной формуле полной
вероятности 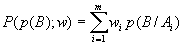 , где
, где 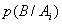 - вероятность события
- вероятность события 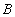 при
условии, что произошло альтернативное событие
при
условии, что произошло альтернативное событие 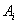 (
(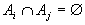 ,
, 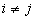 ,
, 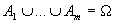
). В этом случае весов-
вой коэффициент
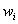 есть вероятность
есть вероятность 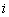 -й
альтернативы
-й
альтернативы 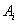 [3].
[3].
Все три указанные задачи приходится
решать, как правило, в условиях дефицита
числовой информации о весовых коэффициентах
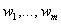 . Дело в
том, что обычно исследователь обладает лишь нечисловой
информацией о весовых коэффициентах,
выражаемой сравнительными суждениями типа
"отдельный показатель
. Дело в
том, что обычно исследователь обладает лишь нечисловой
информацией о весовых коэффициентах,
выражаемой сравнительными суждениями типа
"отдельный показатель 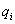 более важен для
определения сводной оценки качества, чем
отдельный показатель
более важен для
определения сводной оценки качества, чем
отдельный показатель 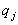 ", "в
", "в 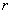 -й финансовый
инструмент надо инвестировать меньше денег, чем
в
-й финансовый
инструмент надо инвестировать меньше денег, чем
в 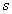 -й
финансовый инструмент", "вероятность
альтернативы
-й
финансовый инструмент", "вероятность
альтернативы 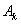 практически равна вероятности
альтернативы
практически равна вероятности
альтернативы 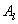 " и т.п. Такая ординальная
(порядковая) информация может быть
представлена в виде системы
" и т.п. Такая ординальная
(порядковая) информация может быть
представлена в виде системы 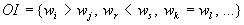 равенств и
неравенств для соответствующих весовых
коэффициентов. Аналогично, неточная
(интервальная) информация о весовых
коэффициентах может быть представлена в виде
системы
равенств и
неравенств для соответствующих весовых
коэффициентов. Аналогично, неточная
(интервальная) информация о весовых
коэффициентах может быть представлена в виде
системы 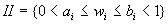 неравенств, определяющих границы
интервалов
неравенств, определяющих границы
интервалов 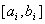 ,
, 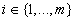 , варьирования
соответствующих весовых коэффициентов.
Учитывая, что зачастую не для всех весовых
коэффициентов
, варьирования
соответствующих весовых коэффициентов.
Учитывая, что зачастую не для всех весовых
коэффициентов 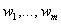 удается задать равенства и
нетривиальные неравенства, ограничивающие
область их варьирования, можно сказать, что в
подобных случаях мы имеем дело с неполной
информацией о весовых коэффициентах. Такая нечисловая,
неточная и неполная информация (ннн-информация)
удается задать равенства и
нетривиальные неравенства, ограничивающие
область их варьирования, можно сказать, что в
подобных случаях мы имеем дело с неполной
информацией о весовых коэффициентах. Такая нечисловая,
неточная и неполная информация (ннн-информация) 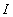 о весовых
коэффициентах
о весовых
коэффициентах 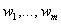 хотя и сужает область допустимых
весовых векторов
хотя и сужает область допустимых
весовых векторов 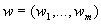 с исходного симплекса
с исходного симплекса 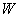 до
некоторого его подмножества
до
некоторого его подмножества 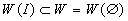 , но не может, как
правило, однозначно выделить единственный
вектор весовых коэффициентов
, но не может, как
правило, однозначно выделить единственный
вектор весовых коэффициентов 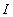 . Иными словами имеет
место неопределенность (дефицит числовой
информации о весовых коэффициентах) - вектор
весовых коэффициентов известен лишь "с
точностью до множества
. Иными словами имеет
место неопределенность (дефицит числовой
информации о весовых коэффициентах) - вектор
весовых коэффициентов известен лишь "с
точностью до множества 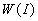 ", содержащего не менее
двух элементов.
", содержащего не менее
двух элементов.
Следуя известной работе Томаса Байеса,
посмертно опубликованной в "Трудах
Королевского общества" в 1763 году, будем
моделировать неопределенность выбора
конкретного вектора весовых коэффициентов
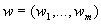 из
множества всех допустимых весовых векторов
из
множества всех допустимых весовых векторов 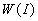 при
помощи рандомизированного (случайного) вектора
весовых коэффициентов
при
помощи рандомизированного (случайного) вектора
весовых коэффициентов 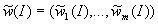 , задаваемого при помощи
некоторого вероятностного распределения на
множестве
, задаваемого при помощи
некоторого вероятностного распределения на
множестве 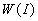 [4]. Тогда в качестве искомой оценки
[4]. Тогда в качестве искомой оценки 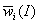
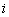 -го весового коэффициента можно
взять, например, математическое ожидание
-го весового коэффициента можно
взять, например, математическое ожидание 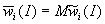 соответствующего рандомизированного весового
коэффициента
соответствующего рандомизированного весового
коэффициента 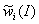 . Теперь вектор полученных оценок
. Теперь вектор полученных оценок 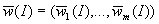 можно
интерпретировать как числовой образ
ннн-информации
можно
интерпретировать как числовой образ
ннн-информации 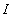 . Мерой точности оценки
. Мерой точности оценки 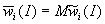 может
служить стандартное отклонение
может
служить стандартное отклонение 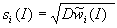
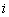 -го случайного весового
коэффициента.
-го случайного весового
коэффициента.
В качестве вероятностного
распределения, моделирующего полное отсутствие
у исследователя информации о значениях весовых
коэффициентов (
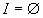 ), можно использовать, следуя,
например, принципу максимальной энтропии [5], равномерное распределение на
симплексе
), можно использовать, следуя,
например, принципу максимальной энтропии [5], равномерное распределение на
симплексе 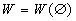 . Тогда получаем естественные оценки
весовых коэффициентов
. Тогда получаем естественные оценки
весовых коэффициентов 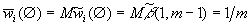 и стандартные отклонения
и стандартные отклонения
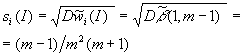
где
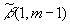 есть случайная величина
есть случайная величина 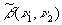 , имеющая
бета-распределение с параметрами
, имеющая
бета-распределение с параметрами 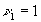 ,
, 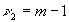 .
.
Посмотрим, как влияет на оценки
весовых коэффициентов наличие у исследователя
нечисловой (ординальной) информации
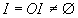 ,
представляющей собой систему неравенств
,
представляющей собой систему неравенств 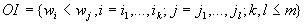 .
Представим эту систему в виде совокупности
следующих цепочек неравенств:
.
Представим эту систему в виде совокупности
следующих цепочек неравенств: 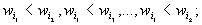
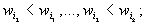
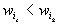 , где
, где 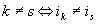 .
Координаты
.
Координаты 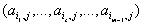 вершины симплекса
вершины симплекса 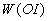 задаются формулой
задаются формулой 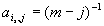 при
при 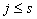 ;
; 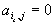 при
при 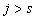 . Эти же вершины
составляют столбцы матрицы
. Эти же вершины
составляют столбцы матрицы 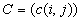 аффинного
преобразования, переводящего симплекс
аффинного
преобразования, переводящего симплекс 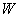 в
симплекс
в
симплекс 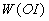 . Отсюда получаем искомые оценки
. Отсюда получаем искомые оценки 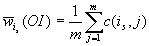 , весовых
коэффициентов и довольно громоздкие формулы для
стандартных отклонений
, весовых
коэффициентов и довольно громоздкие формулы для
стандартных отклонений 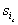 ,
, 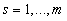 [1].
[1].
Попробуем теперь учесть неточную
(интервальную) информацию, задаваемую системой
неравенств
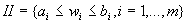 . Заметим, что границы интервалов
варьирования весовых коэффициентов должны быть
предварительно согласованы. Действительно,
нетрудно показать, что из неравенств
. Заметим, что границы интервалов
варьирования весовых коэффициентов должны быть
предварительно согласованы. Действительно,
нетрудно показать, что из неравенств 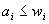 ,
, 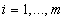 , следуют неравенства
, следуют неравенства 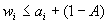 , где
, где 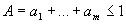 ; а из
неравенств
; а из
неравенств 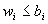 ,
, 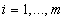 -
неравенства
-
неравенства 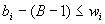 , где
, где 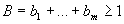 . Поэтому согласованные границы
. Поэтому согласованные границы 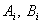 интервалов варьирования весовых коэффициентов
определяются формулами
интервалов варьирования весовых коэффициентов
определяются формулами 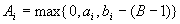 ,
, 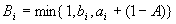 .
.
Случайный вектор
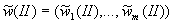 , равномерно
распределенный на симплексе
, равномерно
распределенный на симплексе 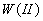 , состоящем из
векторов весовых коэффициентов, удовлетворяющих
системе неравенств
, состоящем из
векторов весовых коэффициентов, удовлетворяющих
системе неравенств 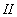 , можно получить в результате
преобразований
, можно получить в результате
преобразований 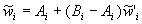 ,
, 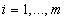 ,
компонент вектора
,
компонент вектора 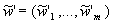 , равномерно распределенного на
симплексе
, равномерно распределенного на
симплексе 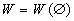 . Отсюда имеем искомые оценки
весовых коэффициентов
. Отсюда имеем искомые оценки
весовых коэффициентов 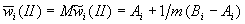 и стандартные отклонения
и стандартные отклонения 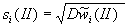 ,
, 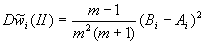 .
.
Итак, изложенная стохастическая
байесовская модель неопределенности задания
весовых коэффициентов позволяет использовать
нечисловую, неточную и неполную информацию
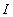 (
(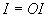 ,
, 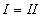 ,
, 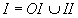 ) для получения числовых
оценок
) для получения числовых
оценок 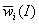 ,
, 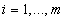 , этих
коэффициентов и для вычисления стандартных
отклонений
, этих
коэффициентов и для вычисления стандартных
отклонений 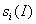 ,
, 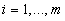 , служащих
показателями точности полученных оценок. В
результате исследователь имеет числовой образ
, служащих
показателями точности полученных оценок. В
результате исследователь имеет числовой образ
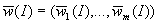 нечисловой,
неточной и неполной информации
нечисловой,
неточной и неполной информации 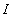 , точность
которого определяется вектором стандартных
отклонений
, точность
которого определяется вектором стандартных
отклонений 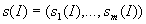 .
.
Подстановка рандомизированного
вектора весовых коэффициентов
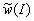 вместо
детерминированного вектора
вместо
детерминированного вектора 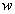 в формулу для
сводного показателя качества
в формулу для
сводного показателя качества 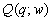 дает
рандомизированный сводный показатель качества
дает
рандомизированный сводный показатель качества 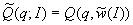 ,
синтезирующий как информацию о значениях
отдельных показателей
,
синтезирующий как информацию о значениях
отдельных показателей 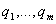 , так и ннн-информацию
, так и ннн-информацию
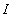 о
значимости этих отдельных показателей качества.
Тем самым, задача сравнения многокритериальных
оценок
о
значимости этих отдельных показателей качества.
Тем самым, задача сравнения многокритериальных
оценок 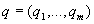 ,
, 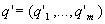 качества
двух сложных объектов сводится к задаче
выявления какого-либо вида стохастического
доминирования между двумя случайными величинами
качества
двух сложных объектов сводится к задаче
выявления какого-либо вида стохастического
доминирования между двумя случайными величинами
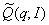 ,
, 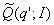 соответственно [3,6].
соответственно [3,6].
Аналогично, подстановка
рандомизированного вектора весовых
коэффициентов
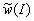 в оценку варианта распределения
ресурса
в оценку варианта распределения
ресурса 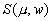 (в оценку
(в оценку 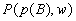 вероятности события
вероятности события 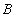 )
порождает рандомизированную оценку варианта
распределения
)
порождает рандомизированную оценку варианта
распределения 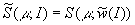 (рандомизированную оценку
(рандомизированную оценку 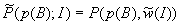 вероятности события
вероятности события 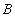 ).
).
Описанная стохастическая байесовская
модель обработки нечисловой, неточной и неполной
информации о весовых коэффициентах служит
основой для так называемого АСПИД-метода (АСПИД -
аббревиатура для "Анализ и Синтез Показателей
при Информационном Дефиците"), реализованного
на ПЭВМ в виде оболочки системы поддержки
принятия решений (ОСППР) АСПИД-3
W [7]. Эта ОСППР нашла широкое применение
для решения разнообразных задач оценки
эффективности и качества многопараметрических
объектов различной природы и назначения (сложных
технических систем, вариантов организационных и
управленческих решений высокого уровня,
коммерческих банков, страховых компаний,
инвестиционных проектов и т.д.) (см., например, [1,3]).
Литература
Хованов Н.В. Анализ и синтез показателей при
информационном дефиците. СПб., 1996.
Первозванский А.А., Первозванская Т.Н.
Финансовый рынок: расчет и риск. М., 1994.
Хованов Н.В. Математические модели риска и
неопределенности. СПб., 1998.
Bayes Th. An essay towards solving a problem in the doctrine of chances // Biometrika.
1958. Vol.45. N3-4.
Levin R. (ed). The Maximum Entropy Formalism. Cambridge, 1979.
Bawa V. Stochastic dominance: a research bibliography // Management Sci. 1981. Vol.28.
Хованов К.Н., Хованов Н.В. Программа для ЭВМ
АСПИД-3W.
Свидетельство РосАПО №960087. 1996.

![]() ,
, ![]() ,
, ![]() , from a fixed set
, from a fixed set ![]() is modeled by a random choice which leads to a
random weight-vector
is modeled by a random choice which leads to a
random weight-vector ![]() distributed on the
set
distributed on the
set ![]() . The set
. The set ![]() being determined by a nnn-information
being determined by a nnn-information ![]() , the vector
, the vector ![]() , where
, where ![]() ,
, ![]() , are mathematical expectations of the
corresponding randomized weight-coefficients, may be treated as a "numeric
image of nnn-information
, are mathematical expectations of the
corresponding randomized weight-coefficients, may be treated as a "numeric
image of nnn-information ![]() ". Some
applications of these models and conceptions to decision-making under uncertainty are
demonstrated.
". Some
applications of these models and conceptions to decision-making under uncertainty are
demonstrated. ![]() ,
,![]() ,
,