С.В.Романов

Санкт-Петербургский государственный электротехнический университет “ЛЭТИ” им.В.И.Ульянова (Ленина)

Разнообразие альтернатив в развитии процесса анализа данных, которые может выбрать исследователь на основании изучения изображений , указывает на поисковый характер решений, на необходимость творческого осмысливания результатов работы любого алгоритма обработки данных.

Большинство специалистов по обработке экспериментальных данных сходятся в том, что разнообразные задачи анализа информации могут быть сведены к трем: классификации исходных данных, выбору информативных признаков, идентификации неизвестных наблюдений. В докладе будут рассмотрены особенности использования структурно – графического интерактивного подхода (1) к реализации двух первых задач анализа.

Схема информационных преобразований данных в классификационной задаче приведена на рис.1.

В общем случае эмпирические данные могут быть сведены в таблицу . Используя различные модели , лежащие в основе методов классификации, исследователь преобразует описание таблицы в вид адекватный этим моделям. В рамках геометрической модели таблицу можно представить в виде совокупности “векторов – строк” (объектов) в признаковом пространстве . Структура “векторов – строк” меняется в зависимости от моделей описания данных . В качестве описаний могут выступать матрицы близости, сходства, подобия (2).

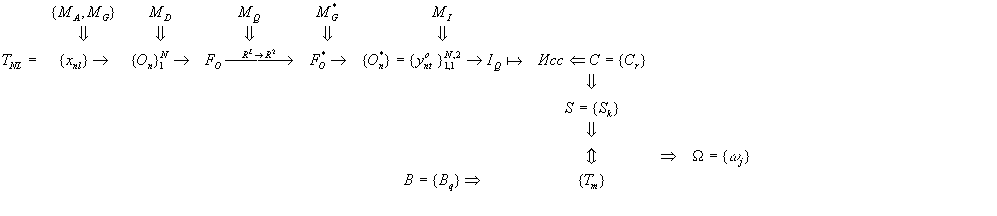
Рис.1

Условием построения образов в пространстве решения является минимальное искажение структурных связей при отображении векторов из пространства в . Условие преобразования исходной структуры в структуру ее образов формализуется в виде:

При проведении научных исследований (особенно в медицине и биологии) в распоряжении исследователя, как правило, имеется обучающая выборка данных, представленная таблицей , а также мнения экспертов о ее возможной классификации . Мнения экспертов могут носить самый общий характер об анализируемом множестве данных (количество ожидаемых классов) или детально интерпретировать принадлежность каждого наблюдения к конкретной группе . В зависимости от этого осуществляется различный уровень сопоставления сформированных классов и априори выделенных групп , а также последующего выбора альтернативных действий по перестройке последовательности информационных преобразований таблицы исходных данных.

Классический подход к оценке информативности параметров исходного описания данных в задаче классификации сводится к следующей процедуре:

- из исходной совокупности параметров

Использование структурно – графического анализа позволяет отказаться от последовательного перебора параметров описания данных в задачах классификации. Такая возможность существует в силу

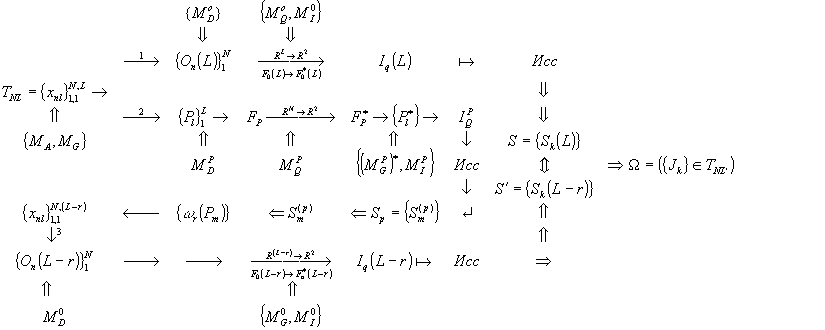
Рис.2

Схема информационных преобразований для оценивания информативности параметров в задаче классификации приведена на рис.2. Эта задача носит многоэтапный характер. На первом этапе во множестве исходных параметров осуществляется разбиение совокупности векторов – объектов на однородные классы в соответствии с методикой описанной ранее.

На втором этапе совокупность исходных параметров разбивается исследователем на однородные группы параметров . В зависимости от моделей описания структур векторов – параметров , алгоритмов преобразования структуры в структуру образов, алгоритмов описания геометрической структуры , моделей и алгоритмов формирования геометрического изображения исследователь формирует совокупность групп однородных параметров . Основным критерием преобразования совокупности параметров в совокупность однородных групп является сохранение близости (коррелированности) исходных векторов – параметров в графическом представлении их образов. В каждой однородной группе параметров исследователь выявляет параметры, стоимость получения которых высока, и исключает их из исходного описания данных. Выбор избыточных для классификационной задачи параметров можно осуществлять одновременно по нескольким однородным группам и совокупности . Наряду со стоимостью получения, могут быть использованы и другие критерии формирования множества избыточных параметров.

На третьем этапе осуществляется отображение в пространство принятия решения совокупности векторов – объектов описанных редуцированным набором параметров . По структуре образов с сохранением ранее использованных алгоритмов и методик строится изображение образов векторов – объектов. Оно разбивается на классы . Сравнивая совокупности классов и , исследователь принимает решения о множестве информативных параметров . Реализация третьего этапа может осуществляться несколькими итерациями. Особенностью этого этапа является то, что, наряду сформированием совокупности информативных для классификации параметров, можно осуществлять отбор параметров ответственных за сохранение структуры классов.

Предложенная методика использовалась для решения широкого класса задач в различных областях науки. В основе ее лежали нелинейные алгоритмы преобразования структур многомерных данных (2).На рис.3 приведен пример иллюстрирующий результат использования предложенной методики для решения реальной задачи медицинской диагностики состояний сердечно-сосудистой системы у детей с нормальным и избыточным весом (две группы пациентов, по 20 человек в каждой). Каждый объект исследования описывался 23 параметрами. На рис.3а представлен графический образ 40 векторов – объектов, описанных в исходном 23-мерном пространстве параметров.

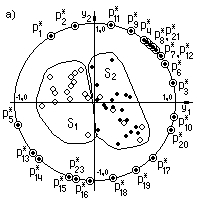
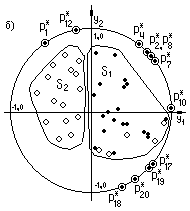
Рис.3

В качестве алгоритмов отображения использовались mapping – алгоритмы 3 типа (2). На основе изучения графического образа подструктуры параметров представленного на рис. 3а, были удалены как неинформативные и избыточные двенадцать из них. Отображение данных, описанных минимизированным объемом параметров (номера их сохранены) представлено на рис.3б. Видно, что удаление избыточных параметров не повлияло на группируемость объектов.

1. Романов С.В. Структурно-графический анализ как метод изучения структур многомерных данных. Настоящий сборник.

2. Романов С. В. Визуализация структур многомерных данных в человеко-машинных распознающих системах. Сборник докладов международной конференции по мягким вычислениям и измерениям SCM-98, T 1, с., 143-147.