A. Yu. Vlasov

Federal Radiological Center, IRH

Mira Street 8, St.-Petersburg, Russia

J.?von?Neumann is considered as one of “fathers” of modern computers due to his theoretical works and elaboration of computer EDVAC at 1945–50, but already 20 year before it, at 1926–31 he participated in drawing yet another kind of logic — logic of quantum mechanics and only now the different areas of research of one scientist seem going to meet and born new family of ultrascale cybernetic devices — quantum computers.

Currently the quantum information science exists mainly as theoretical area of research and size of quantum registers does not exceed of 3-5 quantum bits (qubits), but in the paper is considered question: does the quantum logic has some useful application as an abstract mathematical model in computer science? Such applications of physical models nowadays are not unusual, for example Boltzmann machines and other methods came to area of artificial neural networks from statistical physics [1, 2].

It is also useful to draw some analogy with fuzzy sets and logic [3]. Here is used discrete representation of 2D sets on some lattice due to understanding analogy with bit-map pictures.

Let us introduce few data types in some “Pascal-like” notation to come from fuzzy sets to quantum registers. Here n and N = 2ⁿ are integer numbers.

1) x : dot = [1 .. N,1 .. N];

Here x is represented as point on 2D space for simplicity, because of digitization we can consider space of any dimension as interval of natural numbers x : 1 .. N ². In this example x is visual model for n + n = 2n-bits register.

2) I : set_2D = set of dot;

or

I : set_2D = array [dot] of Boolean;

The set, “image” can be considered as black and white picture - black set on white sheet. It is necessary 2^N·N i.e. 2­ (2­ (2n)) bits for the set.

3) F : fuzzy_set = array [dot] of real;

The real is interval [0.0 .. 1.0] of real numbers represented with some finite precision d. It can be considered as an analogue of gray-scaled picture. The fuzzy set also can be standardized by condition a _xF[x] = 1 where a _x in example under consideration is double sum:

(1)

(in continuous case an integration used instead of the summation and distributions F(x) are used instead of arrays).

The condition (1) is used in statistical interpretation of fuzzy set, when it is suggested to choose some point of set with probability proportional of adequacy function F[x], and sum of all the probabilities is unit. Let us use notation p[x] for the probabilities.

Now let us introduce notion of quantum set (it is not standard term, mathematical object discussed further corresponds to 2n-qubit register in quantum information science [6] or quantum mechanical system with N² states [7]):

4) Q : qu_set = array [dot] of complex;

Where complex is q = u + iw, |q|? 1. Instead of standardization condition here is used normalization : a _x|Q[x]|² = 1 i.e. :

(2)

for example under consideration.

In quantum mechanics the complex numbers q[x] are called amplitudes, related with classical probabilities as p = |q|² = u² + w², i.e. there is standardized fuzzy set related with given normalized quantum set via formula: p[x] = |q[x]|².

It is possible for simplification to consider case with real amplitudes (w = 0), and let us explain why an “auxiliary” fuzzy set with has some independent useful application.

Let us consider two sets p₁[x], p₂[x] and look for some likelihood function H(p₁,p₂) with properties: H(p₁, p₂) < 1 for p_1? p₂, H(p,p) = 1 [1, 3]. For standardized sets such function can be chosen as H(p₁,p₂) = a _x(p₁[x] p₂[x])^1/2. If we use quantum sets q₁, q₂ (p₁=q₁², p₂=q₂²), the formula is H(q₁, q₂) = a _xq₁[x] q₂[x].

In our example x was chosen as multi-index of 2D array mostly for simple visualization and any array can be described as one-dimensional. Here x = (i, j) can be substituted by index of the 1D array like K = (i -1) N + j, K I [1 .. N²], then formula can be written as:

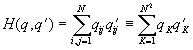(3)

and it shows, that H(q,q? ) is simply scalar product of two vectors with N² elements and unit lengths (due to normalization condition) and so the function really can be unit only for equivalent vectors.

It should be mentioned also, that the formula (3) is given for real q_K for simplicity and in complex case it contains terms with complex conjugation: . It is Hermitian norm [7]. Such case also has applications, for example then we work with complex Fourier transform of some image.

The discussed property of quantum set as “square root of fuzzy set” makes clear, why it can be useful in such abstract area, as image recognition [4, 5], quite far from initial appearance in quantum mechanics.

Let us discuss now some question related with “hardware”. We had few data structures:
1) x : dot, 2) I[x] : set_2D, 3) p[x] : fuzzy_set
It is sequence with more and more complicated structure with occupation of more and more computer memory. But let us suggest, that register x is permanently changing its value by such a law, that after enough period of time T it can be found, the x had value v during time t[v] and .

The algorithm can be implemented by software, but it also can be considered as some hardware register (like implementation of random number generator in some computers with main difference, that p[v] depends on v ; or input port of some analog-to-digital converter is scanning some “physical model” of fuzzy set p).

Then each access to the register produces some value of x with probability p[x], so one 2n-bits stochastic register is enough to implement statistical model of standardized fuzzy set discussed earlier.

Now let us come to qu_set data type. Why it can be modeled by one quantum register? The example with stochastic register as model of fuzzy set is some analogy (see also [8]). But procedure of access to such register due to laws of quantum mechanics has some differences with classical statistical register discussed below.

Let us consider some value q I qu_set of the register, it is array of numbers q[x], we may not read all the numbers, but if we access to the register, we read number x with probability p[x] = |q[x]|² and it coincides with functionality of stochastic register described above.

It should be mentioned only, that any access to q destroys the quantum register by substitution instead of q new array with 1 in element with index x and with all other is 0, and so the register should be reset (preparation in terminology of quantum mechanics) in q after each access (quantum measurement).

But the quantum register has other useful property, it is possible instead of simple access described above to perform another operation, we prepare some given q? I qu_set and read the register q with using q? as some “quantum bit-mask”, then with probability |H(q,q? )|² (see Eq. 3) operation is successful and so by repeating it more times we may found |H| with more precision.

Because the |H| has useful application as likelihood function, the quantum register can be used as some hardware accelerator for image analysis. Currently such hardware is not accessible and so it was interesting to research advantages and disadvantages of the particular function |H| in usual software applications.

It is promising not only because such kind of software would suffer giant speed-up after creation specific quantum hardware, but also because the used mathematical constructions and methods of linear algebra are quite convenient and powerful.

It should be mentioned, that similar mathematical methods already was used in models of associative memory [9] and formal neural network [10] without any relation with quantum mechanical models. Only noticeable difference was using real linear spaces instead of complex and Euclidean norm (Eq. 3) instead of Hermitian (with complex conjugation).

Let us now consider some operations with fuzzy and quantum sets, discuss fuzzy and quantum logic.

For usual sets we have basic operations for A, B : set_2D, - intersection:, union: , complementation: A^c. With using presentation of set as Boolean array the operations in components can be written: (a^c)[x] = not a[x], [x] = a[x]U b[x], [x] = a[x]U b[x].

Similarly it is possible to define operations with fuzzy sets by definition of real analogs of Boolean operations not (¬), and (U ), or (U ).

For example ¬a ®  1-a, aU b ®  min(a,b), aU b ®  max(a,b) is a good choice, but here is used a second one, more algebraic aU b ®  a? b, aU b ®  a+b-ab.

But qu_set introduced above is not directly used in quantum logic — the linear operators are used here instead of vectors:

L: qu_map = array [dot,dot] of complex;
It is matrix for linear map: qu_set ®  qu_set:

or (4)

where indexes I, K are used instead of multi-indexes [i,j] and [k,l] (let us for simplicity use further the indexes like I, K : [1 .. M], M=N²).

The operators A, B,... I qu_map form an algebra with usual matrix multiplication C=AB:

(5)

A special kind of operators, projectors, make possible comparison of the algebra with logic, i.e. Boolean algebra. The projector is operator with property P² = P. Let us consider set of orthogonal projectors, i.e. P_iP_j = 0, i? j, then the operators produce Boolean algebra in respect of operations:

¬P ?  1-P, P/\R ?  PR, P\/R ?  P+R-PR (6)

Elements of the algebra have form P_(S) there S : set of 1 .. M:

(7)

There is relation between qI qu_set and some projector P_qI qu_map : P_q[I,J]=q[I]q[J]. To describe properties of the projector it is convenient together with q considered as row with M elements to consider transposed column q⁺ (conjugated for complex case).

Then P_q= q⁺q and q·q⁺ = H(q,q) = 1 (the row q can be considered as 1? M matrix, column q⁺ as M? 1 matrix and due to law of multiplication the q·q⁺ is 1? 1 matrix i.e. number and q⁺q is M? M matrix) and P_qP_q= q⁺q q⁺q = q⁺1q = q⁺q = P_q.

If we consider family of nonintersected sets q₁, q₂,..., q_k then P_i = q_i⁺q_i are orthogonal projectors and so quantum sets in such representations have rather relations with usual logic than with fuzzy one.

For more clear explanation of properties of P_i it is possible to use existence of some orthogonal (unitary for complex case) matrix U same for all P_i such, that all P? _i = UP_iU ^-1 are diagonal and have very simple form: P? ₁ = diag(1,0,...,0), P? ₂ = diag(0,1,...,0), etc. .

The classical Boolean structure of the operators P_i and their sums P_(S) (see Eq. 7) is because of all the operators commute [11]. If to choose projectors P, R: PR? RP the Eq. 6 do not produce Boolean algebra, but it is other kind of non-Boolean logic, than fuzzy one.

It should be mentioned, that more direct relation with fuzzy set have so-called mixed quantum states R = a _iw_iP_i, a _iw_i = 1 where w_i have statistical nature and so here is written analog of standardized fuzzy set.

A representation of some kind of fuzzy operations is example with family of commuting operators [12], but not projectors. They are described by diagonal matrices: D_q[I,I] = q[I], D_q[I,J] = 0, I? J and already shown Eq. 6.

Bibliographical notes: In addition to references [7, 11] some general handbook on quantum mechanics like [13] is appropriate for most text of the paper. New area of quantum computation is presented in [6, 14–17]. The ‘quant-ph’ and ‘math’ after ‘Report No.’ are quantum physics and mathematics electronic archives of Los Alamos National Laboratory respectively. Two works of J. von Neumann devoted to quantum logic [18] and electronic computers [19] are included for completeness.

1. G. Winkler, Image Analysis, Random Fields and Dynamic Monte Carlo Methods, Springer, 1995
2. B. Kosko, Neural Networks and Fuzzy Systems, Prentice-Hall Int., 1992
3. T. Terno, etc. (editors), Applied Fuzzy Systems, M. Mir, 1993 [Russian, transl. Japanese, Tokyo, 1989]
4. A. Yu. Vlasov, “Quantum Computations and Images Recognition,” Conference QCM’96, Full paper: Report No. quant-ph/9703010
5. A. Yu. Vlasov, “Analogue Quantum Computers for Data Analysis,” Report No. quant-ph/9802028
6. C. H. Bennett, “Quantum Information and Computation,” Physics Today 48 (1995) 24
7. A. I. Kostrikin, Yu. I. Manin, Linear Algebra and Geometry, M. Nauka, 1986 [Russian]
8. R. R. Zapatrin, “Logic Programming as Quantum Measurement”, Int. J. Theor. Phys. 34 (1995) 1813
9. T. Kohonen, Associative Memory: A System- Theoretical Approach, Springer 1978 [M. Mir 1980]
10. E. N. Sokolov, G. G. Vatkyavichus, The neuro-intelligence: from neuron – towards neurocomputer, M. Nauka 1988 [Russian]
11. A. A. Grib, Violation of Bell’s Inequalities and Problem of Measurements in Quantum Theory, JINR preprint P2-92-211, Dubna 1992 [Russian]
12. A. Yu. Vlasov, “Representation and Processing of Information in Quantum Computers,” Tech. Phys. Lett. 20 (1994) 992 [“Представление и обработка информации в квантовых компьютерах,” Письма Ж. Тех. Физ. 20 (1994) 45]
13. Landau and Lifshitz, Course of Theoretical Physics, III (Quantum Mechanics) M. Nauka 1989 [Russian]
14. R. P. Feynman, “Quantum-Mechanical Computers,” Found. Phys. 16 (1986) 507 [Р. Ф. Фейнман, “Квантовомеханические ЭВМ,” УФН 149 (1986) 672]
15. D. Deutsch, “Quantum Theory, the Church-Turing Principle and the Universal Quantum Computer,” Proc. R. Soc. London A 400 (1985), 97
16. D. Deutsch, “Quantum Computational Networks,” Proc. R. Soc. London A 425 (1989), 73
17. D. Deutsch, A. Ekert, R. Lupacchini, “Machines, Logic and Quantum Physics,” (09/11/1999) Report No. math/9911150
18. G. Birkhoff, J. v. Neumann, “The logic of quantum mechanics,” Ann. Math. 37 (1936) 823
19. A. Burks, H. Goldstine, J. v. Neumann, Preliminary discussion of the logical design of an electronic computing instrument, Princeton 1946