 |
||
ЗНАКОВОЕ ДИСКРЕТНОЕ ИЗМЕРЕНИЕ КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ СЛУЧАЙНЫХ ПРОЦЕССОВ
В.Н.Якимов
Самарский государственный технический университет
Abstract - The report describes the algorithms of measurement of autocorrelation function and cross-correlation function of casual processes. These algorithms are based on stochastic sign conversion using evenly distributed auxiliary signal. The result of conversion is considered as analog-to-digital time lags conversion. The time lags are determined as intervals between successive fronts of sign signal.
Экспериментальный анализ случайных процессов во многих случаях требует измерения корреляционных и взаимных корреляционных функций. В настоящее времени разработано достаточно большое количество методов и средств корреляционных измерений. При этом широкое распространение получили цифровые методы измерения. Однако алгоритмы измерения корреляционных характеристик, разработанные на основе классических цифровых методов преобразования реализаций исследуемых случайных процессов, не всегда позволяют вести качественную оперативную обработку исходных данных. В соответствии с этим все возрастающий объем экспериментальных исследований и объективная необходимость сокращения времени их проведения требуют постоянного повышения эффективности корреляционного анализа.
Один из путей решения указанной проблемы связан с разработкой цифровых алгоритмов первичного дискретного преобразования непрерывных процессов не только позволяющих повысить скорость получения результатов измерения чисто технически за счет простого увеличения производительности обработки дискретных выборок, но и осуществляющих предварительную обработку исходной информации на стадии формирования цифровых отсчетов.
Упростить процедуры цифровой обработки случайных процессов позволяет знаковые методы измерения корреляционных зависимостей с использованием вспомогательных случайных сигналов
[1,2]. При этом задача знакового преобразования сводится к воспроизведению знака реализации первичного процесса, взвешенной относительно вспомогательного сигнала на интервале времени измерения. Такое преобразование эквивалентно первичному цифровому преобразованию с ограниченным двухуровневым стохастическим квантованием.Пусть сформированы знаковые сигналы
![]() (1)
(1)
![]() (2)
(2)
где
Sgn{...} - оператор функции знакового преобразования;Вспомогательные сигналы
Основную сложность при практической реализации знакового преобразования представляет генерирование вспомогательных сигналов с заданным законом распределения. Наиболее просто и реально получение вспомогательных сигналов с равномерным законом распределения. В этом случае мгновенные значения вспомогательных сигналов
![]() и
и ![]() (3)
(3)
где
Оценку
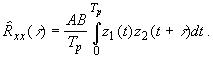 (4)
(4)
Длительности знаковых сигналов
Результат знакового преобразования можно рассматривать
как поток фронтов прямоугольных импульсов со случайной флуктуацией интервалов их длительности. Данному потоку фронтов будет свойственна зависимость их временного положения от совпадения по уровню мгновенных значений реализации исследуемого случайного процесса и вспомогательного случайного сигнала [3]. Тогда в процессе преобразований (1) и (2) достаточно знать только мгновенные значениеПусть известны моменты времени, в которые сигналы
![]() - для сигнала
- для сигнала ![]() ; (5)
; (5)
![]() - для сигнала
- для сигнала ![]() ; (6)
; (6)
![]() (7)
(7)
Учитывая, что сигнал
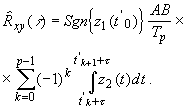 (8)
(8)
Введем обозначения
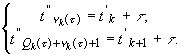 (9)
(9)
Величины
С учетом обозначений (9) сигнал
![]() (10)
(10)
которые принадлежат множеству (6).
Принимая во внимание, что сигнал
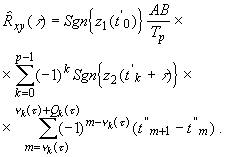 (11)
(11)
В последнем выражении внутренняя сумма представляет собой сумму интервалов
Значения величин
![]() (12)
(12)
где
T0 - период следования тактовых импульсов.В результате будем иметь:
![]() и
и ![]() - цифровые эквиваленты значений
моментов времени
- цифровые эквиваленты значений
моментов времени ![]() и
и ![]() ;
;
![]() - задержка в целочисленном коде.
- задержка в целочисленном коде.
В соответствии с этим для (9) справедливо следующее
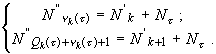 (13)
(13)
В свою очередь, целочисленные значения величин из множества (10) будут равны
![]() (14)
(14)
Тогда если одну из величин
A, B, Tp или T0 выбрать таким образом, чтобы при целом n выполнялось условие![]() (15)
(15)
то оценка взаимной корреляционной функции (11) примет вид
 (16)
(16)
Внутренняя сумма в выражении (16) может быть частично просуммирована. В результате этого будем иметь
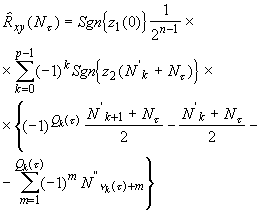 (17)
(17)
Алгоритмы (16) и (17) измерения взаимной корреляционной функции
Следует также отметить, что вся процедура вычисления взаимной корреляционной функции
Методика измерения корреляционной функции
Rxx(t ) случайного процессаЛитература
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|