 |
||
ОПТИМИЗАЦИЯ НЕЧЕТКОГО АЛГОРИТМА УПРАВЛЕНИЯ МОТОРОМ С ПОМОЩЬЮ НЕЙРОСЕТИ
А.Н.Аверкин
1, К.В.Сулин21
Вычислительный центр Российской академии наук,2
Московская государственная академия приборостроения и информатикиAbstract – The optimization of fuzzy control algorithm for motors using neural network model is considered.
Применение нечеткого управления, основанного на эвристическом подходе в формировании закона управления к системам невысокого порядка, обеспечивает простую и быструю реализацию и настройку системы управления. Желаемое качество переходного процесса регулирования может быть достигнуто как изменением внутренних параметров регулятора, так и за счет изменения входных и выходных коэффициентов усиления регулятора. В ряде случаев нечеткий регулятор обеспечивает более высокие показатели качества переходных процессов по сравнению с классическими законами. К большому преимуществу нечеткого управления следует отнести его ориентацию на цифровую реализацию.
Системы подобного рода обладают достаточно большой гибкостью и хорошими качествами переходного процесса — минимального времени выхода рабочего органа на заданную позицию с минимальным перерегулированием. Однако результаты работы регулятора заметно ухудшаются, если параметры системы активно изменяются во времени.
В настоящее время существует несколько методов настройки и адаптации нечетких регуляторов к системам, в которых они используются. Одним из наиболее прогрессивных является метод, основанный на применении нейросетевых моделей. Наиболее широко распространена генерация функций принадлежности переменных с помощью нейросетей [1], [2].
Однако, в системах, работающих в режиме реального времени существует необходимость обучения и адаптации управляющего блока в зависимости от режима работы. В этом случае генерация функций принадлежности в процессе работы может привести к ухудшению контроля над системой в силу сложности вычислительного алгоритма и замедления реакции на изменение входных параметров. Кроме того, аппаратная реализация такого метода потребует довольно мощных вычислительных ресурсов и, соответственно, увеличит себестоимость системы регулирования.
Более перспективным с точки зрения быстроты настройки является алгоритм, основанный на использовании многозначных нечетких логик, позволяющий настроить нечеткий регулятор на логику пользователя или близкую к ней без изменения функций принадлежности и блока правил. В основе многозначных логик лежат обобщенные операторы конъюнкции и дизъюнкции, получившие название Т-норм и Т-конорм [3]. Существует достаточно большое количество подобных операторов и их семейств, поэтому актуальна задача их подбора для конкретных реализаций нечетких регуляторов. Практика показала, что изменение логики работы контроллера ощутимо сказывается на результатах управления и значительно менее требовательно к аппаратным ресурсам, чем методы, описанные выше.
Рассмотрим более подробно задачу управления электроприводом. На данный момент уже существуют реализации моделей фаззи-контроллеров, работающих с использованием t-нормы и двойственной ей t-конормы Минимума ТМ
и МаксимумаSМ : TM(x,y) = min (x,y); SM(x,y) = max(x,y);
Произведения Т
P и Вероятностной суммы SP : TP(x,y) = x Ч y, SP(x,y) = x + y - x Ч y;t-нормы
TL и t-конормы SL Лукасевича :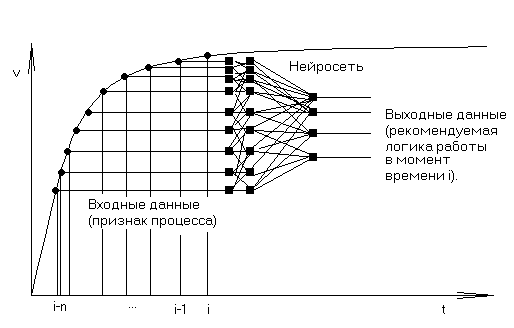 TL(x,y) =
max(x + y - 1,0), SL(x,y) = min(x + y,1);
семейства t-норм
TL(x,y) =
max(x + y - 1,0), SL(x,y) = min(x + y,1);
семейства t-норм ![]()
и t-конорм ![]() Франка
:
Франка
:
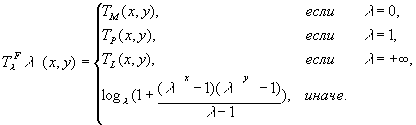
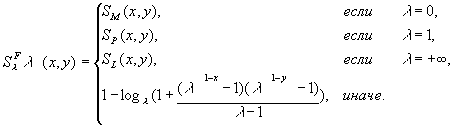 Разработка оказалась вполне
жизнеспособной, однако моделирование регулятора
определило новый круг задач, связанных с
оптимизацией подбора Т-норм и Т-конорм. Наиболее
значимыми из них являются следующие:
Разработка оказалась вполне
жизнеспособной, однако моделирование регулятора
определило новый круг задач, связанных с
оптимизацией подбора Т-норм и Т-конорм. Наиболее
значимыми из них являются следующие:
Представляется, что можно выделить 5 скоростных режимов работы электропривода: а. Начальный разгон (запуск); б. Полный останов; в. Ускорение; г. Замедление; д. Стабильный режим (с постоянной скоростью).
Для определения режима работы системы можно воспользоваться данными о скорости вращения ротора, снимаемыми с датчиков через определенные интервалы времени. Имея некоторое количество таких значений, можно сделать вывод о состоянии системы. Для решения этой задачи можно воспользоваться нейросетью, входными значениями которой будет n последних показаний датчика, а выходными – рекомендуемая логика работы (Рис.1).
Рис. 1. Анализ текущего скоростного режима с помощью нейросети.
Разумеется, нейросеть должна быть заранее обучена на различных выборках показаний датчиков скорости ротора. Для обучения можно использовать алгоритм обратного распространения без привлечения экспертов. Критерием оптимальности использования той или иной логики работы регулятора в заданном скоростном режиме является наибольшее соответствие требуемой и реальной угловой скорости ротора.
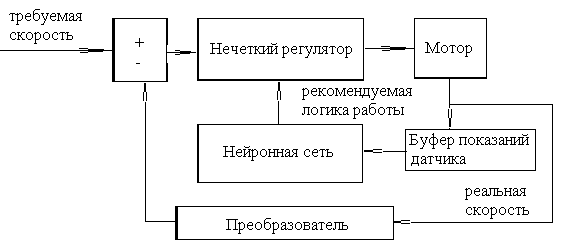
Рис.2.
Предлагаемая реализация системы управления электроприводом.![]()
![]() Учитывая
вышеперечисленные пункты, проводится
моделирование системы в реальном времени и
разрабатывается программное обеспечение,
представляющее собой экспертную систему,
позволяющую создавать и обучать нейросетевые
структуры для распознавания скоростных режимов,
визуализировать процесс работы системы
посредством построения графиков скорости
ротора, а так же позволяющую давать
сравнительные характеристики для разных логик
работы регулятора в различных скоростных
режимах.
Учитывая
вышеперечисленные пункты, проводится
моделирование системы в реальном времени и
разрабатывается программное обеспечение,
представляющее собой экспертную систему,
позволяющую создавать и обучать нейросетевые
структуры для распознавания скоростных режимов,
визуализировать процесс работы системы
посредством построения графиков скорости
ротора, а так же позволяющую давать
сравнительные характеристики для разных логик
работы регулятора в различных скоростных
режимах.
![]()
![]()
![]()
![]()
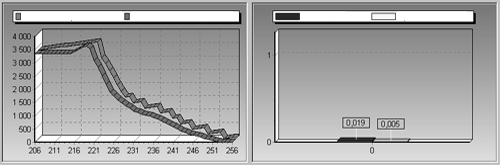
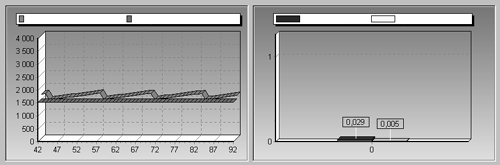 Рис.
3. Графики требуемой и реальной скоростей ротора.
Режим постоянной скорости. Вероятностная логика.
Рис.
3. Графики требуемой и реальной скоростей ротора.
Режим постоянной скорости. Вероятностная логика.
![]()
![]() Рис. 4. Графики
требуемой и реальной скоростей
ротора. Режим замедления. Логика Лукасевича.
Рис. 4. Графики
требуемой и реальной скоростей
ротора. Режим замедления. Логика Лукасевича.
Как видно из приведенных графиков, качество управления действительно зависит от используемой логики работы и скоростного режима. Это подтверждает то, что существующие алгоритмы управления еще далеки от совершенства и созданные на их основе контроллеры нуждаются в доработке.
Таким образом, можно сделать вывод о том, что применение нейросетевых моделей в автоматическом управлении электроприводом в сочетании с уже используемыми методами, основанными на нечетких алгоритмах даст положительный результат и позволит существенно улучшить точность и надежность функционирования управляемой системы.
Литература
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|