2Санкт-Петербургский государственный университет

линейной непрерывной стационарной системы обусловлена нечеткостью коэффициентов А_к характеристического многочлена А(р), являющихся нечеткими числами А_к = a m (a _ki)/ a _ki

Необходимое условие устойчивости такой системы состоит в положительности всех коэффициентов А_к. Это означает, что в случае устойчивости среди элементов a_ki множеств А_к отсутствуют положительные и все a _ki > 0

Если n= 3, то согласно известным критериям Рауса и Гурвица [1] условие устойчивости кроме (2) выражается равенством А₁ А₂ – А₀ А_{3 >} 0 или

А₀ = 0,5/4 + 1/5 + 0,5/6,

А₂ = 0,5/2 + 1/3 + 0,5/4,

А₁ = 0,5/8 + 1/10 + 0,5/12,

А₃ = 0,5/0,5 + 1/1 + 0,5/1,5. (3)

Получив нечеткие произведения П₁ = А_{1 ·} А₂ и П ₂ = А_{0 ·} А₃ , найдено нечеткое множество (3) в виде нечеткого частного П₁ / П₂ = y . Нечеткие множества П₁ и П₂

- это декартовые произведения А₁ · А₂ , А₀ · А₃ с элементами a_1i a_2j, a_0i a_3j и функциями принадлежности m (a_1i a_2j) = m (a_1i) U m (a_2j), m (a_0i a_3j) = m (a_0i) U m (a_3j). Нечеткое множество y - это декартово произведение П₁ х П₂ с элементами I_1i : I_2j и функциями принадлежности m (I_1i : I_2j) = m (I_1i) U m (I_2j).

Если согласно (3) множества А_к трехэлементные, то П₁ и П₂ множества девятиэлементные, а y = { y _1…. y _81} - множество с числом элементов равным 9².

Различны элементы y нечеткого множества y соответствуют различным динамическим системам. Таким образом, нечеткая передаточная функция (1) данными нечеткими коэффициентами (5) описывает множество С= { ©₁,…, ©_81} различных систем с. Для заключения об устойчивости этих систем при А_к > 0 необходимо и достаточно:

В случае n=3 и (3) имеем miny = 1,8 > 1.

Условия устойчивости систем ©, составляющих множество С, описываемое нечеткой передаточной функцией (1) по Раусу или Гурвицу, резко усложняется с увеличением n и числа элементов нечетких множеств А_к. Поэтому в общем случае при n = 4 рекомендуется применение грубого критерия устойчивости [2, 3], требующего составления ряда отношений четких и нечетких коэффициентов характеризиристического многочлена А(р)

и ряды вторичных отношений

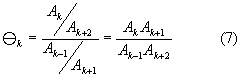Согласно этому критерию необходимым условием устойчивости являются неравенства Ак > 0, y _к > 1

Достаточными условиями устойчивости являются неравенства, при n = 4:

y _к ? 2; к = 1,2 , при n ? 5: y _к ? 2,15; к = 1, n -1 ,

Условиями достаточными для устойчивости в случае Ак > 0 при n = 4 являются неравенства:

min y _{к >} 2, к = 1,2;

и при n ? 5 – неравенства:

min y _к ? 2,15, к = 1, (n-1).

А₀ = 1/6 + 0,5/7 А₄ = 1/8 + 0,6/10

А₁ = 0,8/4,8 + 1/5,2 А₅ = 0,7/0,6 + 1/0,7

А₂ = 0,3/28 + 1/29 А₆ = 0,5/0,25 + 1/0,6

А₃ = 1/6 + 0,8/8

min y ₁ = 2,4, min y ₂ = 3,2

min y ₃ = 2,4 min y ₄ = 2,4

min y ? 2,015

Если оказывается, что среди (8) имеется хоть одно значение min y ₅ в пределах от 1 до 2,15, то это означает, что среди © есть хоть один элемент, расположенный в относительной близости к границе устойчивости.

1. Постинков М.М. Устойчивые многочлены. – М.: Наука, 1981. – 176 с.
2. Соколов Н.И., Липатов А.В. О некоторых достаточных условиях устойчивости и неустойчивости линейных непрерывных стационарных систем // Автоматика и телемеханика, № 9 , 1978. с-30-37.
3. Лебедев А.Н. Грубый критерий устойчивости. – Л: ЛЭТИ, 1981. Депонировано в ВИНИТИ, № 624 – 82 Деп+. – 52 с.