 |
||
О нахождении минимального представления контура изображения как решение задачи нечеткой кластеризации
А.Е. Лепский
Таганрогский государственный радиотехнический университет
Abstract - The most important field in the image processing is a problem of classification the contours of gray-level imagines. An effective approach to solve this problem is to use control points that gives us the vector description of the contour. The most task in the image analysis is a problem of extraction the minimal set of control points. The image may be considered as a fuzzy set. In this paper the task finding of minimal representation of control points set is solved with the help of fuzzy clustering (by E.Ruspini).
Важной областью в теории
искусственного интеллекта является задача
классификации контуров плоских бинарных
изображений. Один из способов решения этой
задачи состоит в выделении на распознаваемом
контуре ![]() некоторого
упорядоченного подмножества точек
некоторого
упорядоченного подмножества точек ![]() . Этому множеству точек ставятся в
соответствии упорядоченные наборы (векторы)
признаков
. Этому множеству точек ставятся в
соответствии упорядоченные наборы (векторы)
признаков ![]() выделенных
точек. В процессе обработки и интерпретации
контурных изображений приходится сталкиваться с
тем или иным типом неясностей. Источниками
неясностей могут быть расплывчатость исходных
изображений, дискретизация изображений в
процессе их обработки и.д. Поэтому множество
точек контура
выделенных
точек. В процессе обработки и интерпретации
контурных изображений приходится сталкиваться с
тем или иным типом неясностей. Источниками
неясностей могут быть расплывчатость исходных
изображений, дискретизация изображений в
процессе их обработки и.д. Поэтому множество
точек контура ![]() можно
рассматривать как нечеткое множество с функцией
принадлежности
можно
рассматривать как нечеткое множество с функцией
принадлежности ![]()
Конкретизируем эту задачу для
получения минимального представления множества
признаков контура. Под контуром ![]() будем понимать нечеткое множество
точек с односвязным носителем, на котором задано
отношение порядка. В первую очередь на контуре
стараются выделить так называемые угловые
(контрольные) точки, то есть точки, имеющие
большую кривизну. Если
будем понимать нечеткое множество
точек с односвязным носителем, на котором задано
отношение порядка. В первую очередь на контуре
стараются выделить так называемые угловые
(контрольные) точки, то есть точки, имеющие
большую кривизну. Если ![]() -
гладкий контур, заданный параметрически
-
гладкий контур, заданный параметрически ![]()
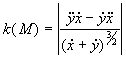 .
Кривизну дискретного контура можно оценить
косвенно, например (см. [2]), следующим образом. На
универсальном множестве
.
Кривизну дискретного контура можно оценить
косвенно, например (см. [2]), следующим образом. На
универсальном множестве 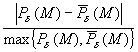 назовем весом точки
назовем весом точки Заметим, что ![]() .
Далее, для некоторого фиксированного значения
.
Далее, для некоторого фиксированного значения ![]() выделим множество
выделим множество ![]()
![]() .
Множество
.
Множество ![]() является
некоторым представление контура
является
некоторым представление контура ![]() . Возникает задача выбора значений
параметров
. Возникает задача выбора значений
параметров ![]()
Вычисление минимального представления нечеткого множества является задачей нечеткой кластеризации. Основные пути решения задач нечеткой классификации были рассмотрены в ряде работ E.H.Ruspini (см. обзор в [4, стр.114-132]). Один из подходов к нечеткой кластеризации состоит в определении на множестве всех возможных представлений некоторых функционалов, которые затем оптимизируются для получения желаемой кластеризации.
Будем рассматривать представление ![]() контура
контура ![]()
![]() .(1)
.(1)
Эффективность такой кластеризации
зависит от используемого нечеткого отношения
похожести ![]() , а выбор
этого отношения определяется признаками, по
которым осуществляется классификация. В
частности, в качестве отношения похожести можно
использовать функцию
, а выбор
этого отношения определяется признаками, по
которым осуществляется классификация. В
частности, в качестве отношения похожести можно
использовать функцию ![]()
![]() , где
, где ![]()
![]()
![]() (2)
(2)
Нетрудно показать, что если ![]() , то (2) заведомо
выполняется. Таким образом, задача состоит в
максимальном уменьшении мощности множества
, то (2) заведомо
выполняется. Таким образом, задача состоит в
максимальном уменьшении мощности множества ![]() (при увеличении
(при увеличении ![]() ) до тех пор, пока (2) не
перестанет выполняться. Так как (2) верно для всех
) до тех пор, пока (2) не
перестанет выполняться. Так как (2) верно для всех ![]() , то, учитывая, что
, то, учитывая, что ![]() , если
, если ![]() , имеем
, имеем
![]()
![]() . (3)
. (3)
Поэтому представление ![]() должно удовлетворять следующему
условию
должно удовлетворять следующему
условию
![]()
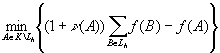 . (4)
. (4)
В частности, если ![]() - четкое множество (
- четкое множество (![]() для всех
для всех ![]() ) и
) и ![]() , то (4) приобретает вид
, то (4) приобретает вид
![]() , (5)
, (5)
где ![]() -
мощность множества
-
мощность множества ![]() .
Непосредственно из определения нечеткого
.
Непосредственно из определения нечеткого ![]() представления множества
представления множества ![]() и оценки (2) следует
справедливость следующих предложений
и оценки (2) следует
справедливость следующих предложений
Предложение 1. Если ![]() является нечетким
является нечетким ![]() представлением множества
представлением множества ![]() с отношением похожести
с отношением похожести ![]() , то справедлива оценка
, то справедлива оценка
![]() . (6)
. (6)
Предложение 2. Если ![]() для всех
для всех ![]() и для
некоторого множества
и для
некоторого множества ![]() выполняется
(6), то
выполняется
(6), то ![]() - нечеткое
- нечеткое ![]() представление множества
представление множества ![]() с отношением похожести
с отношением похожести ![]()
Будем говорить, что неравенство (6)
выполняется точно на ![]() ,
если для любой функции
,
если для любой функции ![]() ,
такой что существует
,
такой что существует ![]()
![]() . (7)
. (7)
Предложение 3.
Если (6) выполняется точно для нечеткогоДоказательство непосредственно
следует из определения точной оценки (7) и
неравенства (2), где ![]()
Через ![]()
![]() обозначим подмножество
нечеткого
обозначим подмножество
нечеткого ![]() представления
представления
![]() множества
множества ![]() , имеющее наименьшую мощность.
, имеющее наименьшую мощность.
Предложение 4. Пусть ![]() - четкое множество. Справедливо следующее
утверждение:
- четкое множество. Справедливо следующее
утверждение: ![]() для всех
для всех ![]() тогда и только тогда,
когда
тогда и только тогда,
когда ![]()
Доказательство. Необходимость. Если ![]() для всех
для всех ![]()
Достаточность.
ПустьРассмотрим алгоритм нахождения
минимального представления ![]() . Пусть
. Пусть ![]() -
множество точек контура
-
множество точек контура ![]()
![]() и
и ![]()
![]()
для ![]() . Тогда,
согласно (4), минимальное
. Тогда,
согласно (4), минимальное ![]() , для которого
, для которого ![]() ,
будет определять границу разбиения множества
,
будет определять границу разбиения множества ![]() на два класса
на два класса ![]() и
и ![]() . Если
. Если ![]() - четкое
множество, то алгоритм нахождения минимального
представления
- четкое
множество, то алгоритм нахождения минимального
представления ![]() значительно
упрощается. Пусть
значительно
упрощается. Пусть ![]() и
и ![]()
![]() ,
, ![]() . Тогда наименьшее
. Тогда наименьшее ![]() , для которого
, для которого ![]() будет определять границу представления
будет определять границу представления ![]() .
.
Пример: пусть ![]() - четкое множество и
- четкое множество и ![]() , где
, где ![]()
![]()

Замечание. В качестве отношения
похожести можно использовать также функцию ![]()
![]() ,
, ![]() , которая, в силу справедливости
неравенства
, которая, в силу справедливости
неравенства ![]() для
для ![]() , удовлетворяет всем
условиям отношения похожести. Так как
, удовлетворяет всем
условиям отношения похожести. Так как ![]() при
при ![]() , то очевидно, для минимального
, то очевидно, для минимального ![]() представления
представления ![]() будет справедливо
включение
будет справедливо
включение ![]() , если
, если ![]() .
.
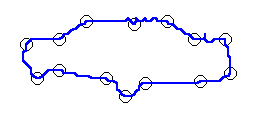
При практическом использовании предложенного метода для выделения контрольных точек контура нужно дополнить алгоритм проверкой некоторых дополнительных условий. Например, желательно, чтобы контрольные точки контура не располагались близко друг к другу. Результат работы алгоритма нахождения минимального представления методом нечеткой кластеризации показан на следующих рисунках: рис.1 – исходное изображение объекта, отделенное от фона; рис.2 – внешний контур объекта; рис.3 – контрольные точки контура, выделенные методом нечеткой кластеризации.

Литература
1. Каркищенко, А.Н., Броневич А.Г. Вероятностные и возможностные методы классификации случайных последовательностей/ Таганрог: ТРТУ, 1996. 193 с.
2. Каркищенко А.Н., Лепский А.Е., Безуглов А.В. Об одном способе векторного и аналитического представления контура изображения// Известия ТРТУ. Тематический выпуск. Интел. САПР, Таганрог: ТРТУ, 1998, №2(8), с.107-111.
3. Лепский А.Е. Кривизна и вес точки контура плоского изображения объекта// Материалы Всерос. науч.-техн. конф. “Компьютерные технологии в инж. и упр. дяетельности, Таганрог: ТРТУ, 1999, с. 21-22.
4. Нечеткие множества и теория возможностей. Последние достижения/ под ред. Р.Р.Ягера, М., Радио и связь, 1986.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|