КОМПОЗИЦИЯ НЕЧЕТКИХ МНОЖЕСТВ И ЕЕ
ПРИМЕНЕНИЕ К ПРИНЯТИЮ РЕШЕНИЙ
В.И. Левин
Пензенский технологический институт
Abstract - A Generalization of Operations
with fuzzy Sets is considered. Application of new Operation to Decision making is given.
Использование непрерывной логики (НЛ)
с несущим множеством
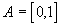 и логическими операциями
и логическими операциями 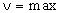 (дизъюнкция),
(дизъюнкция), 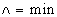 (конъюнкция) и отрицание
(конъюнкция) и отрицание 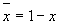 позволяет обобщить теоретико-множественные
операции на случай нечетких множеств [1]
позволяет обобщить теоретико-множественные
операции на случай нечетких множеств [1]
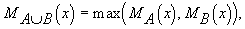
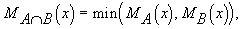 (1)
(1)
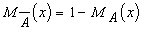 .
.
Здесь
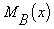 - мера принадлежности
элемента
- мера принадлежности
элемента 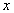 множеству
множеству 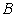 . Операции объединения и
пересечения нескольких нечетких множеств
вводятся аналогично (1).
. Операции объединения и
пересечения нескольких нечетких множеств
вводятся аналогично (1).
Операции объединения и пересечения
нечетких множеств (1) есть обобщение на случай
нечетких множеств операций объединения и
пересечения обычных множеств, путем
использования известных операций НЛ - дизъюнкции
и конъюнкции. Использование новых операций,
обобщающих НЛ - логических определителей (ЛО)
дает семейство новых операций над нечеткими
множествами, не имеющих аналогов среди операций
над обычными множествами и более полно отражает
расплывчатый характер границ нечетких множеств.
Введем конечное множество
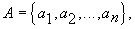 (2)
(2)
в котором
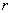 -й по величине элемент есть
-й по величине элемент есть
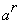 ,
так что
,
так что 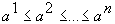 . Функцию
. Функцию
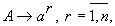 (3)
(3)
назовем порядковым ЛО ранга
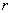 и
обозначим
и
обозначим 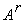 или
или 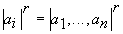 . ЛО
. ЛО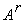 является числовой характеристикой
множества
является числовой характеристикой
множества 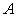 , напоминающей определитель
квадратной матрицы. Он выражается через свои
элементы при помощи операций НЛ в виде (2)
, напоминающей определитель
квадратной матрицы. Он выражается через свои
элементы при помощи операций НЛ в виде (2)
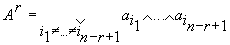 .(4)
.(4)
Рассмотрим конечную совокупность
нечетких множеств
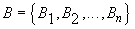 . (5)
. (5)
Введем над этой совокупностью
семейство операций
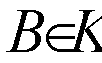 , (6)
, (6)
определяемых следующим соотношением
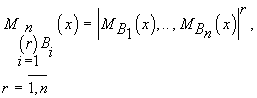 (7)
(7)
Введенную операцию
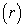 назовем
назовем 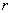 -композицией
нечетких множеств
-композицией
нечетких множеств 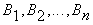 . Таким образом, мера принадлежности
элемента
. Таким образом, мера принадлежности
элемента 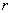 -композиции нечетких множеств
определяется как порядковый ЛО ранга
-композиции нечетких множеств
определяется как порядковый ЛО ранга 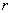 от
совокупности мер принадлежности этого элемента
отдельным множествам. В частном случае
от
совокупности мер принадлежности этого элемента
отдельным множествам. В частном случае 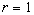 получаем
1-композицию множеств, совпадающую с их
пересечением. В другом частном случае
получаем
1-композицию множеств, совпадающую с их
пересечением. В другом частном случае 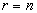 получаем
получаем 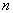 -композицию
множеств, совпадающую с их объединением. В общем
случае, при
-композицию
множеств, совпадающую с их объединением. В общем
случае, при 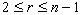 (который реализуется, если
(который реализуется, если 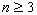 )
) 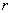 -композиция является новой
операцией, существенно отличающейся как от
объединения, так и от пересечения нечетких
множеств. Точнее говоря, эта операция занимает
промежуточное положение между операциями
объединения и пересечения, что вытекает из
очевидных неравенств
-композиция является новой
операцией, существенно отличающейся как от
объединения, так и от пересечения нечетких
множеств. Точнее говоря, эта операция занимает
промежуточное положение между операциями
объединения и пересечения, что вытекает из
очевидных неравенств
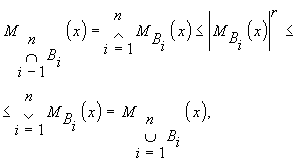 (8)
(8)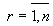
Как видно из (8), операция
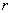 -композиции
нечетких множеств сильнее операции их
объединения, но слабее операции их пересечения
(т.е.
-композиции
нечетких множеств сильнее операции их
объединения, но слабее операции их пересечения
(т.е. 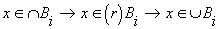 ). При этом по мере увеличения
). При этом по мере увеличения 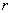 от 1 к
от 1 к 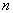 "сила"
"сила" 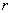 -композиции уменьшается,
приближаясь к силе операции объединения
множеств, а по мере уменьшения
-композиции уменьшается,
приближаясь к силе операции объединения
множеств, а по мере уменьшения 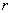 от
от 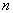 к 1 эта "сила"
возрастает, стремясь к "силе" операции
пересечения множеств.
к 1 эта "сила"
возрастает, стремясь к "силе" операции
пересечения множеств.
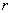 -композиция нечетких множеств,
являясь обобщением операций объединения и
пересечения таких множеств, может быть в то же
время представлена в виде суперпозиции
указанных операций. Действительно, раскрыв ЛО в
правой части (7) согласно (4), получаем
-композиция нечетких множеств,
являясь обобщением операций объединения и
пересечения таких множеств, может быть в то же
время представлена в виде суперпозиции
указанных операций. Действительно, раскрыв ЛО в
правой части (7) согласно (4), получаем
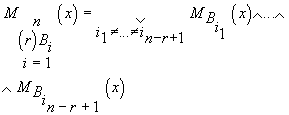
(9)
Но согласно (1) конъюнкции (дизъюнкции)
НЛ мер принадлежности элемента нечетких
множеств соответствует пересечение
(объединение) этих множеств. Поэтому из (9) следует
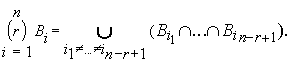 (10)
(10)
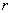 -композиция нечетких множеств
удовлетворяет распределительному закону
относительно пересечения и объединения и закону
сложной (повторной) композиции [3].
-композиция нечетких множеств
удовлетворяет распределительному закону
относительно пересечения и объединения и закону
сложной (повторной) композиции [3].
Введенная операция
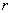 -композиции нечетких
множеств не является обобщением операций с
обычными множествами и не переходит в них при
переходе нечетких множеств в четкие. Она
является новой операцией, не имеющей аналогов
среди обычных теоретико-множественных операций.
Операция
-композиции нечетких
множеств не является обобщением операций с
обычными множествами и не переходит в них при
переходе нечетких множеств в четкие. Она
является новой операцией, не имеющей аналогов
среди обычных теоретико-множественных операций.
Операция 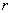 -композиции показывает, что между
объединением и пересечением множеств нет
пропасти, обе они -
-композиции показывает, что между
объединением и пересечением множеств нет
пропасти, обе они - 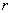 -композиции с различными значениями
индекса
-композиции с различными значениями
индекса 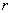 . Благодаря существенной новизне
операции
. Благодаря существенной новизне
операции 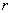 -композиции появляется возможность
более эффективного логического вывода и
принятия решений.
-композиции появляется возможность
более эффективного логического вывода и
принятия решений.
Рассмотрим вопрос подробнее. Пусть
имеется коллектив из
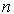 экспертов, оценивающих
одну и ту же ситуацию количественно, в условиях
неполной информации. Предположим, что оценка
ситуации, даваемая одним экспертом, имет вид
нечеткого подмножества
экспертов, оценивающих
одну и ту же ситуацию количественно, в условиях
неполной информации. Предположим, что оценка
ситуации, даваемая одним экспертом, имет вид
нечеткого подмножества 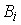 множества всех
альтернатив и характеризуется соответствующей
мерой принадлежности
множества всех
альтернатив и характеризуется соответствующей
мерой принадлежности 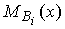 . Тогда задача состоит в
объединении (агрегировании) оценок различных
экспертов в единую, коллективную оценку
изучаемой ситуации. Обычным подходом при
объединении индивидуальных оценок в
коллективную оценку является пересечение
нечетких подмножеств
. Тогда задача состоит в
объединении (агрегировании) оценок различных
экспертов в единую, коллективную оценку
изучаемой ситуации. Обычным подходом при
объединении индивидуальных оценок в
коллективную оценку является пересечение
нечетких подмножеств 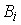 , с получением нового
нечеткого множества
, с получением нового
нечеткого множества
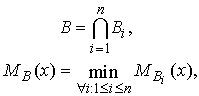 (11)
(11)
которое и принимается за коллективную
оценку ситуации
[4].
недостаток оценки (11) в узости и разреженности
(малой мере 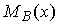 ) получаемого оценочного множества,
которое может оказаться и пустым, если
индивидуальные оценки
) получаемого оценочного множества,
которое может оказаться и пустым, если
индивидуальные оценки 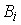 сильно различаются.
Возможный выход из положения заключается в том,
чтобы отказаться от требования выбирать в
качестве коллективной оценки общую часть всех
индивидуальных оценок (как это принято в (11)), и
заменить его более мягким условием выбора в
качестве коллективной той индивидуальной
оценки, которую дает наиболее
"представительный" эксперт. В качестве
такого эксперта естественно выбрать того, чья
оценка достаточно удалена от крайних оценок,
имеющихся в данном коллективе. Таким образом,
предлагаемый подход означает объединение
индивидуальных оценок в коллективную путем
операции
сильно различаются.
Возможный выход из положения заключается в том,
чтобы отказаться от требования выбирать в
качестве коллективной оценки общую часть всех
индивидуальных оценок (как это принято в (11)), и
заменить его более мягким условием выбора в
качестве коллективной той индивидуальной
оценки, которую дает наиболее
"представительный" эксперт. В качестве
такого эксперта естественно выбрать того, чья
оценка достаточно удалена от крайних оценок,
имеющихся в данном коллективе. Таким образом,
предлагаемый подход означает объединение
индивидуальных оценок в коллективную путем
операции 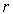 -композиции над ними с подходящим
значением ранга
-композиции над ними с подходящим
значением ранга 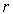
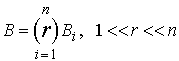 . (12)
. (12)
Результат этой операции и принимается
за коллективную оценку изучаемой ситуации.
Наш подход можно назвать ранговым. Как
следует из (10), ранговый подход эквивалентен
выделению всевозможных "представительных
подмножеств" экспертов по
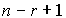 эксперту в каждом, и
принятию в качестве коллективной наилучшей (с
максимальным
эксперту в каждом, и
принятию в качестве коллективной наилучшей (с
максимальным 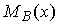 ) из оценок, полученных в
подмножествах по правилу (11).
) из оценок, полученных в
подмножествах по правилу (11).
Литература
Заде Л. Понятие лингвистической переменной. - М.:
Мир, 1978.
Левин В.И. Структурно-логические методы
исследования сложных систем с применением ЭВМ. -
М.: Наука, 1987.
Левин В.И. Обобщенные операции над
нечеткими множествами// International Conference
on Soft Computing and Measurements. Proceedings of Conference. Vol.1. S-Petersburg. 1999.
Bellman R.E., Zadeh L.A. Decision making in Fuzzy Environment// Management
Science. 1970. V.17. №4.

![]()
![]() (1)
(1)![]() .
.![]() (2)
(2)![]() (3)
(3)![]() .(4)
.(4)![]() . (5)
. (5)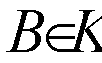 , (6)
, (6)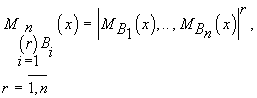 (7)
(7)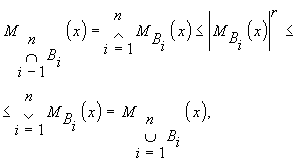 (8)
(8)![]()
![]() -композиция нечетких множеств,
являясь обобщением операций объединения и
пересечения таких множеств, может быть в то же
время представлена в виде суперпозиции
указанных операций. Действительно, раскрыв ЛО в
правой части (7) согласно (4), получаем
-композиция нечетких множеств,
являясь обобщением операций объединения и
пересечения таких множеств, может быть в то же
время представлена в виде суперпозиции
указанных операций. Действительно, раскрыв ЛО в
правой части (7) согласно (4), получаем 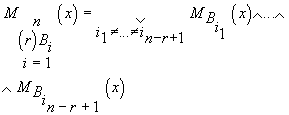
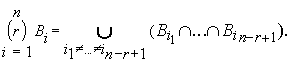 (10)
(10)![]() -композиция нечетких множеств
удовлетворяет распределительному закону
относительно пересечения и объединения и закону
сложной (повторной) композиции [3].
-композиция нечетких множеств
удовлетворяет распределительному закону
относительно пересечения и объединения и закону
сложной (повторной) композиции [3].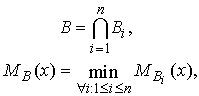 (11)
(11)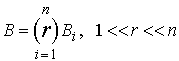 . (12)
. (12)