L.V. Utkin, I.B. Shubinsky

St. Petersburg Forest Technical Academy

Cai Kai-Yuan et al. [1] have introduced the profust (probabilistic behavior - fuzzy states) reliability theory. According to the theory, systems cannot be simply viewed as failed or non-failed in a large variety of cases. Therefore, the system success and failure should be characterized by fuzzy [10] states. At any time the system can be viewed as being in one of the two fuzzy states. At the same time the system failure behavior is fully characterized in the context of the probability measures. To analyze such systems the fuzzy state is described by a membership function [2] which can be determined in advance according to some appropriate, e.g. objective manner. The approach presented in [1] assumes that probabilities of the system crisp states are known. However, it is difficult sometimes to obtain these probabilities and only bounds of levels of performance are known. Moreover, results of [1] are based on condition of the component independence. This judgement is a strong structural constraint that should be justified and not taken for granted as often takes place. Therefore, new methods are needed to analyze the reliability of such systems taking into account the partial ignorance about state probabilities and absence of information about independence of the system components.

One of the most promising tools for reliability and risk assessments by partial information is the Walley’s theory of coherent imprecise probabilities [8] (also called the theory of lower previsions, the theory of interval statistical models [3]). A general framework for the theory of imprecise probabilities is provided by upper and lower previsions of gambles. They can model a very wide variety of kinds of uncertainty, partial information, and ignorance. Upper and lower previsions can be regarded as upper and lower expectations of gambles. The rules used in the theory of lower previsions, which are based on a general procedure called natural extension, can be applied to various measures, including possibility and probability measures.

Some results concerning the imprecise reliability have been shown in [4-7]. In the present paper, application of the imprecise probability theory to reliability of systems with fuzzy states are studied.

Let us briefly review the basic concepts of the theory of imprecise probabilities. All definitions and results introduced in this section can be found in [8,9]. A gamble is a bounded real-valued quantity whose value is uncertain. The lower prevision of , denoted by , is a real number which is interpreted as a supremum buying price for . An upper prevision can be defined by and is interpreted as an infimum selling price for . It is often natural to regard and as lower and upper bounds for some ideal price that is not known precisely. Upper and lower probabilities of an event are defined to be upper and lower previsions of its indicator function. They are related by , where denotes the complement of . Upper and lower previsions can be regarded as generalizations of upper and lower probabilities. To model complete ignorance the vacuous previsions and are used.

Natural extension is a general mathematical procedure for calculating new previsions from initial judgements. For computing new previsions and from an available set of previsions and , , the natural extension can be used in the form:

,

subject to

,

and

,

subject to

.

It should be noted that inequalities must be valid for all values .

In fact, the natural extension can be regarded as a linear programming problem with variables , .

Suppose that a component has m non-fuzzy states . On the set of all states we can define a fuzzy operating (success) state and a fuzzy failed state . Thus, each state S_i  can be considered both success and failed. For the membership functions of the component there holds . The probability that the component is in the operating state at instant t is determined as follows:

,

where p_i(t) is the probability that the component is in state S_i  at time t and E is the expectation operator.

The probability that the component is in the failed state at instant t is determined as follows:

,

Suppose that we do not know the state probabilities p_i(t). However, we can obtain lower  and upper bounds of mean levels of component performance or lower and upper probabilities of the fuzzy operating state from experts. Thus functions and  can be regarded as gambles. The functions  and can be regarded as lower and upper previsions, i.e. ,, , . To model complete ignorance the vacuous previsions  and can be used.

A complex system may consist of n components with fuzzy states. This implies that the system reliability measures can be determined by means of the natural extension. For computing the lower prevision  from an available set of the component previsions  and , i=1,...,n, the natural extension can be used in the following form:

, (1)

subject to

.

Here  is a membership function of a system fuzzy operating state. Note that the above problem is dual one to the following linear optimization problem:

subject to

, .

Here the infimum is taken over the set of all probability distributions that are consistent with the given information, i.e. they satisfy the above constraints. The presented problem is more explainable from the probabilistic point of view.

If the system components are independent, then . However, the optimization problem becomes nonlinear in this case. The above explains why problem (1) allows us to take into account the lack of information about the component independence.

For computing the upper prevision from an available set of the component previsions  and , i=1,...,n, the natural extension can be used in the following form:

, (2)

subject to

.

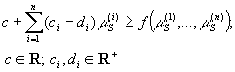So, new previsions  and can be computed as a solution to the linear programming problem. However, the linear programming computations will become impracticable when the number of components in the system is large. Therefore, we will consider several special cases, for which natural extensions can be computed explicitly, without linear programming.

It should be noted that previsions  and are obtained without the judgement of conditional dependence or independence of the system components. This possibility can be important when we are ignorant about conditional dependence. Indeed, it is difficult sometimes to decide in advance whether components are dependent or not.

In the following, we shall omit variable t for brevity.

A system is said to be typical if the system failure and the component failures satisfy some typical relationship. This definition can be naturally extended to systems with fuzzy states [1]. The system with fuzzy states is said to be typical if some typical relationships lie between the system failure membership function and the component failure membership functions and between the system success membership function and the component success membership functions. Define a parallel, series, and mixture systems.

A system is referred to as a series system if it satisfies the following relation:

.

Theorem 1. For the series system, there hold

,

.

Proof: It follows from constraints of problem (1) that inequality holds. Let us write a tangent equation to the surface at the point , , as

.

Hence for any value of i there hold

, , .

Then the objective function can be written as . By substituting into constraints, we can conclude that . Let us show that there exists a solution for which . The solution is

,.

The upper bound is proved similarly.

Another way for representing the system membership function of a series system is

.

Theorem 2. For the series system, there hold

,

.

The proof of Theorem 2 can be found in [7].

A system is referred to as a parallel system if it satisfies the following relations:

.

Theorem 3. For the parallel system, there hold

,

.

Another way for representing the system membership function of a parallel system is

.

Theorem 4. For the parallel system, there hold

,

.

A system is taken to be a mixture system if it satisfies the following relation:

.

Theorem 5. For the mixture system

,

.

The proofs of Theorems 3,4,5 are obvious and follow from proofs of Theorems 1,2.

From the above results, the following conclusion can be made. For the series, parallel, mixture systems, the lower and upper mean levels of system performance are independent of the membership functions of the component fuzzy states.

The research of this work was partially supported by the Ministry of Education of the Russian Federation.

1. K.Y.Cai, C.Y.Wen, M.L.Zhang. Fuzzy states as a basis for a theory of fuzzy reliability. Microelectronics and Reliability. 33, 2253-2263, 1993.
2. D.Dubois and H.Prade. Possibility Theory: An Approach to Computerized Processing of Uncertainty. Plenum Press, New York, 1988.
3. V.P.Kuznetsov, Interval Statistical Models. Radio and Communication, Moscow, 1991. (in Russian).
4. L.V.Utkin. General reliability theory on the basis of upper and lower previsions. Fuzzy Logic and Intelligent Technologies for Nuclear Science and Industry. Proc. of the 3^rd Int. FLINS Workshop. Antwerp, Belgium, 36-43, 1998.
5. L.V.Utkin, S.V.Gurov. Steady-state reliability of repairable systems by combined probability and possibility assumptions. Fuzzy Sets and Systems. 97, 193-202, 1998.
6. L.V.Utkin, S.V.Gurov. New reliability models on the basis of the theory of imprecise probabilities. Proc. of the 5^th Int. Conf. on Soft Computing and Information/Intelligent Systems. Iizuka, Japan, 656-659, 1998.
7. L.V.Utkin, S.V.Gurov. Imprecise reliability of general structures. Knowledge and Information Systems. 1(4), 459-480, 1999.
8. P.Walley. Statistical Reasoning with Imprecise Probabilities. Chapman and Hall, London, 1991.
9. P.Walley. Measures of uncertainty in expert systems. Artificial Intelligence, 83, 1-58, 1996.
10. L.A.Zadeh. Probability measures of fuzzy events. J. Math. Anal. a. Appl., 23, 421-427, 1968.