 |
||
Анализ планОВ действий интеллектуальных агентов с применением логических моделей параллельных процессов
Л.К. Птицына, Н.В. Соколова, С.М. Шестаков
Санкт-Петербургский Государственный Технический Университет
Abstract – This article presents an approach for intellectual agent plans analysis. We analyze information-gathering plans for an intellectual agent working in heterogeneous networks. Our approach is based on logical models of parallel processes adopted for stochastic environment. We calculate time and cost distributions of typical information-gathering queries and analyze such characteristics as average time, average cost and probability of plan execution within given time and cost constraints.
В современных гетерогенных сетях наблюдается быстрый рост количества разнородных информационных источников. Всё большую популярность завоевывает подход к организации сбора информации из таких источников на базе интеллектуальных информационных агентов.
Известные системы сбора информации, построенные с применением теории планирования (
XII, TSIMMIS, SAGE, Occam, Infomaster, Information Manifold), не учитывают в достаточной мере стохастический характер гетерогенных сетей, а также не содержат адекватных математических моделей, учитывающих возможности по распараллеливанию сбора информации.Для эффективного планирования действий информационных агентов необходимо построение математических моделей, приспособленных для анализа временных и стоимостных характеристик последовательно-параллельных планов в стохастических средах
[1],[2]. В настоящем докладе рассмотрим два типовых случая опроса, представляющих особый интерес - последовательный опрос двух и более информационных источников, а также параллельный опрос двух и более информационных источников.Для простоты изложения считается, что информационные источники идеальны, т.е. вероятность неуспешного выполнения запроса к каждому источнику принимается равной нулю. В зависимости от приоритетности запроса при планировании необходимо балансировать временные и стоимостные характеристики информационных планов. Например, для срочных запросов можно строго ограничить время выполнения, но разрешить потреблять большое количество системных ресурсов. Фоновые запросы могут быть строго
ограничены по системным ресурсам, но занимать значительное время.Для анализа временных и стоимостных характеристик при выполнении типовых опросов информационных источников построены модели, ориентированные на случай оценки следующих характеристик:
- среднего времени выполнения запроса;
- вероятности того, что время выполнения запроса не превысит заданное;
- средней стоимости выполнения запроса (потребляемых системных ресурсов);
- вероятности того, что стоимость выполнения запроса не превысит заданную.
Оценки временных и стоимостных характеристик при выполнении типовых опросов информационных источников с ограничениями определены посредством анализа построенных моделей. Базовым компонентом модели является элемент отображения запроса к одному информационному
источнику. Предполагается, что запрос к информационному источнику выполняется успешно с вероятностью 1. Причем временной интервал t, через который станет известен результат выполнения запроса, является случайной величиной, распределенной по некоторому закону. При анализе осуществляется дискретизация времени ожидания завершения запроса с некоторым квантом D t и принимается во внимание ограниченное время дискретных наблюдений Kmax. Ожидаемое количество квантов до завершения запроса рассматривается как дискретная случайная величина (ДСВ) k. Дискретное распределение вероятностей времени завершения запроса представляется через f(k). Для распределения f(k) должно выполняться следующее условие:![]() , k=1,2,..., Kmax
. (1)
, k=1,2,..., Kmax
. (1)
При исследовании проводится квантование стоимости запроса с некоторым интервалом D
C и учитывается ограничие стоимости Mmax квантами. Ожидаемая стоимость запроса обозначается C, а дискретное распределение вероятностей стоимости запроса - f(C). Для распределения f(C) должно выполняться условие:![]() , C=1,2,..., Mmax
. (2)
, C=1,2,..., Mmax
. (2)
На основе известных для каждого информационного источника распределений (1), (2) построена графовая модель типового запроса, удовлетворяющая определению логической модели процесса
[3]. С помощью известных методов анализа логических моделей последовательно-параллельных процессов [4],[5] получены оценки распределения вероятностей времени и стоимости выполнения типового запроса. Для отыскания выбранных характеристик использован оригинальный программный продукт, предназначенный для анализа логических моделей параллельных процессов. Применительно к решаемой задаче задействованы метод отыскания групп совместных вершин и метод свертки [3]. Кроме того, для оценки выбранных характеристик методом свертки получены аналитические соотношения.Вероятность
P(k_? Nmax) того, что к заданному моменту Nmax опрос будет завершен определяется по рассчитанному с помощью известных соотношений [4],[5] итоговому распределению вероятностей F_(k_) времени выполнения типового запроса k_:![]() . (3)
. (3)
Соответственно, среднее время опроса вычисляется как математическое ожидание случайной величины
k_:![]() . (4)
. (4)
Аналогично по итоговому распределению вероятностей стоимости выполнения типового запроса
F_(C_) определяется вероятность P(C_? Cmax) того, что стоимость опроса не превысит заданного порогового значения Cmax, и средняя стоимость типового опроса MO[C_]:![]() ; (5)
; (5)
![]() . (6)
. (6)
Рассмотрен общий случай последовательного опроса
I информационных источников. Для каждого элементарного запроса заданы распределения вероятностей времени выполнения fj[kj]; j=1,...,I, причем kj=1,...,Mjmax . Методом свертки получены следующие соотношения для вычисления итогового распределения времени выполнения типового запроса:![]() ;
;
k12...j=min(k1+k2+...+kj),...,
max(k1+k2+...+kj) ;
(7)
j=1,...,I;
![]() ;
;
k_=min(k1,k12,...,k12...I),..,max(k1,k12,...,k12...I).
Аналогично рассмотрен общий случай параллельного опроса (логическая функция "И")
I информационных источников. Для вычисления итогового распределения времени выполнения типового запроса методом свертки получены следующие соотношения: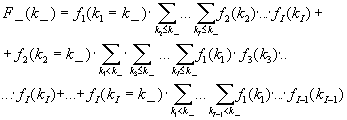 (8)
(8)
i=1,2,…,I .
Соотношения для вычисления итоговых распределений стоимости типовых запросов получены путём подстановки в (7) и (8) известных распределений стоимости опроса каждого информационного источника
fj[Сj], j=1,...,I, Cj=1,...,Сjmax вместо соответствующих распределений времени.Исходные данные для каждого элементарного запроса получены на основе анализа статистики выполнения запросов к информационным источникам существующих корпоративных сетей. Первый вариант соответствует обращению к информационному источнику, обладающему следующими свойствами: высокая производительность; высокая стоимость ресурсов; доступ по высокоскоростному каналу. Второй вариант связан с информационным источником, которому присущи средняя производительность; невысокая стоимость ресурсов; доступ по высокоскоростному каналу. Третий вариант характеризует обращение к информационному источнику со сверхвысокой производительностью; сверхвысокой стоимостью ресурсов, доступ к которому осуществляется по низкоскоростному каналу. Четвертый вариант - средняя производительность; высокая стоимость ресурсов; доступ по низкоскоростному каналу. Исходные данные для представленных вариантов приведены в табл.1 и 2.
Табл. 1.
Исходные распределения вероятностей времени выполнения запроса
k |
f1(k) |
f2(k) |
f3(k) |
f4(k) |
1 |
0.09764 |
0.05166 |
0.01298 |
0.01187 |
2 |
0.15824 |
0.08487 |
0.07467 |
0.04513 |
3 |
0.16835 |
0.14575 |
0.31168 |
0.06413 |
4 |
0.15319 |
0.17527 |
0.32142 |
0.11638 |
5 |
0.12626 |
0.18450 |
0.11363 |
0.18527 |
6 |
0.10606 |
0.15498 |
0.06818 |
0.23752 |
7 |
0.08585 |
0.08671 |
0.04870 |
0.19714 |
8 |
0.05387 |
0.06273 |
0.02597 |
0.09738 |
9 |
0.03535 |
0.03321 |
0.01298 |
0.02850 |
10 |
0.01519 |
0.02032 |
0.00979 |
0.01668 |
Табл. 2.
Исходные распределения вероятностей стоимости выполнения запроса
C |
f1(C) |
f2( С) |
f3(C) |
f4(C) |
1 |
0.00175 |
0.00262 |
0.00207 |
0.00377 |
2 |
0.01757 |
0.13123 |
0.00828 |
0.01886 |
3 |
0.14059 |
0.34120 |
0.06211 |
0.23584 |
4 |
0.26362 |
0.20997 |
0.16563 |
0.24528 |
5 |
0.24604 |
0.10498 |
0.31055 |
0.20754 |
6 |
0.12653 |
0.06561 |
0.24844 |
0.11509 |
7 |
0.08084 |
0.04986 |
0.09316 |
0.06603 |
8 |
0.05975 |
0.05511 |
0.05797 |
0.05094 |
9 |
0.03690 |
0.02624 |
0.03105 |
0.03396 |
10 |
0.02641 |
0.01318 |
0.02074 |
0.02269 |
Для описанных вариантов построены временные и стоимостные модели следующих типовых запросов:
При анализе выделенных ситуаций введены два варианта ограничений по времени и стоимости, соответствующие различной приоритетности запроса:
(а) срочный запрос - допустима высокая стоимость, но требуется быстрое выполнение. Ограничения для примера 1.:
Nmax = 20; Cmax = 30, ограничения для примера 2.: Nmax = 6; Cmax = 9.(б) фоновый запрос: - требуется низкая стоимость, но допустимо медленное выполнение. Ограничения для примера 1:
Nmax = 30; Cmax = 20, ограничения для примера 2.: Nmax = 9; Cmax = 6.Результаты, полученные методом отыскания совместных вершин, представлены в табл.3.
Табл. 3.
Экспериментальные оценки характеристик для примеров 1-2
Показатель |
Приоритетность запроса |
|
Срочный |
Фоновый |
|
2.1. Последовательный опрос четырех источников |
||
| P(k_? Nmax) | 0,66305 |
0,99731 |
| MO[k_] | 18,94204 |
|
| P(С_? Сmax) | 0,99614 |
0,61461 |
| MO[С_] | 19,72182 |
|
2.2. Параллельный опрос четырех источников |
||
| P(k0? Nmax) | 0,38463 |
0,93942 |
| MO[k_] | 6,98133 |
|
| P(С_? Сmax) | 0,91948 |
0,44867 |
| MO[С_] | 6,95353 |
|
Оценка искомых характеристик по методу свертки показала результаты, идентичные приведенным в табл.3. Выявленный факт инвариантен относительно характера исходных данных для рассматриваемых моделей.
Результаты экспериментов свидетельствуют, что представленный подход позволяет получить оценки характеристик информационных планов. Полученные оценки могут быть использованы при проведении сравнительного анализа планов для выбора среди них наиболее эффективного в условиях заданных ограничений по стоимости и времени. При анализе можно варьировать временные и стоимостные ограничения. Представленный подход представляется перспективным для анализа более сложных планов сбора информации в гетерогенных сетях, в том числе опроса реплицированных информационных источников, опроса информационных источников с учетом их возможных отказов, и анализа таких характеристик, как вероятности преодоления априорной неопределенности и вероятности успешного выполнения плана.
Литература
1. Птицына Л.К., Шестаков С.М.
Проектирование интеллектуальных агентов для гетерогенных сетей // Материалы межвузовской научной конференции "Пятьдесят лет развития кибернетики", СПбГТУ, 1999г. - СПб, 1999. - С.81-82.2.
Добрецов С.В., Шестаков С.М. Планирование действий в искусственном интеллекте // Вестник Академии Технического Творчества "ДЕМИУРГ", №1 за 1998 г. - СПб, 1998. - С.32-46.3. Соколова Н.В. Анализ временных характеристик параллельных
вычислительных процессов с задержками комплексирования последовательных фрагментов. // Вестник Молодых Ученых. №1(2) за 1999 г. - СПб, 1999. - С.81-87.4.
Головкин Б.А. Расчет характеристик и планирование параллельных вычислительных процессов. - М.: Радио и связь, 1983. - 272 с.5.
Птицына Л.К., Цыган В.Н. Программное обеспечение ЭВМ: Уч.пособие. - Л.:ЛГТУ, 1991. - 92 с.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|