К РАСЧЕТУ ТОПОЛОГИЧЕСКОЙ ПЛАСТИЧНОСТИ ЯДЕРНЫХ НЕЙРОННЫХ СЕТЕЙ

К расчету топологической пластичности ядерных нейронных сетей

А.Ю. Дорогов

Санкт-Петербургский государственный электротехнический университет “ЛЭТИ” им В.И.Ульянова (Ленина)

Abstract – In the article the quantitative evaluation of topological plasticity neural networks is considered. The exact formulas and asymptotic evaluations are obtained. The example of calculation of topological plasticity degree is indicated.

Ядерные нейронные [1,2] сети относятся к многослойным сетям прямого распространения. Наполнение класса осуществляется за счет целенаправленного ограничения связей между нейронами. К классу ядерных сетей принадлежат как многослойные классические персептроны, так и быстрые нейронные сети [3], со структурой подобной алгоритмам БПФ. Между двумя полярными классами лежит множество нейронных сетей, структуру которых можно варьировать в зависимости от целевого приложения. Выбор подходящей структуры является наиболее сложной задачей при проектировании ядерной сети. Поэтому определяющую значимость имеют количественные оценки проектируемых структур. Одна из таких оценок – “топологическая пластичность” – рассматривается в настоящей работе.

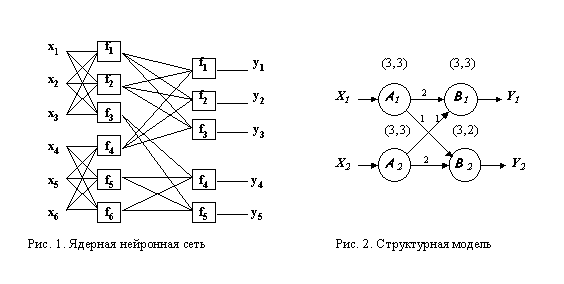
Идеология ядерных сетей основана на понятии нейронного ядра. Нейронное ядро можно рассматривать как однослойный персептрон малой размерности. Нейронные ядра локализуются в пределах нейронного слоя и имеют непересекающиеся рецепторные поля. На рис.1 показан пример двухслойной ядерной нейронной сети, где каждая вершина соответствует формальному нейрону. Показанный граф полностью определяет топологию связей нейронной сети, поэтому данное представление будем называть топологической реализацией. Каждое ядро на структурном уровне характеризуется размерностью рецепторного поля и числом входящих в него нейронов, т.е. определяется парой чисел , где - размерность рецепторного поля, а - число нейронов в данном ядре.

Для ядерной нейронной сети достаточным структурным описанием может служить ориентированный граф, в котором каждая вершина соответствует одному нейронному ядру, а дуги отвечают операторам межъядерных связей. Такой граф называются структурной моделью ядерной сети. На рис.2 показан пример структурной модели для топологической реализации, представленной на рис.1. На графе структурной модели показаны веса вершин и веса дуг. Вес вершины определяется структурной характеристикой ядра , а вес дуги равен рангу проектирующего оператора межъядерной связи.

Обратный переход от структурной модели к топологической реализации неоднозначен, что можно трактовать как свойство топологической пластичности ядерной нейронной сети. Степень топологической пластичности будем оценивать мощностью множества топологических реализаций отвечающих данной структурной модели.

Рассмотрим метод расчета степени топологической пластичности на примере двухслойной ядерной нейронной сети. Обозначим нейронные слои символами и . Каждому нейронному слою соответствует пара множеств , где - множество рецепторов слоя, а - множество нейронов. Топологию нейронной сети можно задать через топологию нейронных ядер и топологию межслойного перехода. Топология нейронного ядра определяется топологией его рецепторного и аксонового полей. Топологии рецепторных полей первого слоя и топологии аксоновых полей аксоновых полей последнего поля не зависят от межслойных связей и поэтому могут быть рассмотрены отдельно. Рассмотрим вначале топологии рецепторных полей первого слоя. Нейронные ядра делят рецепторное поле первого слоя на непересекающиеся подмножества:

где - размерность рецепторного поля ядра , - количество ядер в слое . - размерность рецепторного поля первого слоя и выполнено условие: .

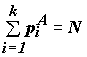Все множество топологий рецепторного поля можно получить, произвольным образом выбирая разбиения множества на подмножества. Будем считать, что две топологии рецепторных полей совпадают, если они имеют одинаковый состав подмножеств . Пронумеруем все рецепторы числами от до . Тогда разбиению рецепторного поля нейронного слоя по нейронным ядрам будет соответствовать разбиение числового множества , а переход от одной топологии к другой можно рассматривать как перестановку на числовом множестве с указанным разбиением. Упорядоченный набор чисел обозначим через , и будем называть композицией топологии. Перестановки образуют симметрическую группу порядка , а множество различающихся топологий представляет собой орбиту композиции . Длину орбиту можно вычислить по формуле расчета числа “перестановок с повторениями” [4]. Таким образом, число различных топологий будет равно:

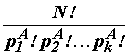
Для расчетов обычно используют информационную меру

(1)

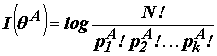
которая называется информацией разбиения [5]. Аналогичные рассуждения для аксоновых полей выходного слоя приводят к выражению:

, (2)

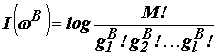
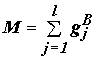где - количество ядер в слое , композиция топологии аксонового поля слоя , - число нейронов в выходном слое, причем .

Рассмотрим теперь топологию межслойного перехода. Обозначим через

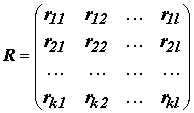
ранговую матрицу, определяющую межслойные связи. Поскольку рецепторные поля не пересекаются, то

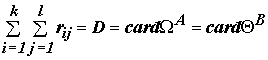
Выполнены также условия:

, и .

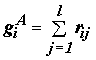
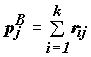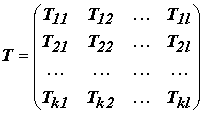
Топология аксоновых полей слоя и топология рецепторных полей слоя взаимозависимы, что обусловлено наличием связей между ними. Можно предложить следующий алгоритм построения топологий. Разместим числовое множество в виде матрицы

которая подобна ранговой матрице в том смысле, что для элементов матрицы выполняются условия .

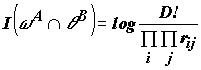
Если собрать все подмножества по строкам, то получим разбиение числового множества, определяющее топологию аксоновых полей слоя . Аналогично объединение подмножеств по столбцам определяет топологию рецепторного поля слоя . Очевидно, что перестановки элементов в пределах подмножеств не изменяют топологию межслойного перехода. Взаимную зависимость топологию будем трактовать как пересечение композиций смежных полей. Вновь используя формулу расчета числа “перестановок с повторениями” получим информационную меру:

, (3)

которая определяет длину орбиты топологий межслойного перехода. Суммируя выражения (1)(2)(3) окончательно получим информационную оценку степени топологической пластичности двухслойной сети:

В качестве примера выполним расчет для структуры нейронной сети, показанной на рис.2.

Таким образом, степень топологической пластичности для данной структурной модели будет равна

Для аналитического анализа степени пластичности удобно использовать приближенные асимптотические выражения, основанные на известной формуле Стирлинга для факториалов:

где .

Используя это приближение для выражения (1) получим:

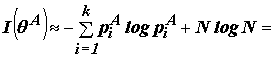
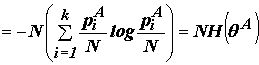
где

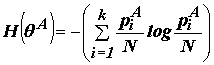
энтропия разбиения. Аналогично из формул (2)(3) получим:

На основе полученных выражений нетрудно определить условия, при которых топологическая пластичность будет принимать максимальные значения. Поскольку функция энтропии принимает максимальные значения при равенстве слагаемых суммы, то максимум пластичности будет достигнут при выполнении условий:

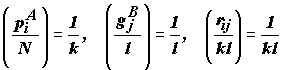
для любых . Следовательно

, ,

. (4)

Для рассмотренного примера

Подставляя эти значения в формулы (4) получим: Откуда степень пластичности для всей сети будет равна . Это значение может служить верхней оценкой достижимой топологической пластичности для данной структурной модели.

Представленный в данной статье метод расчета топологической пластичности позволяет сравнивать между собой структурные модели ядерных нейронных сетей. Интуитивно можно предположить, что чем выше степень топологической пластичности, тем выше способность нейронной сети адаптироваться к внутренней структуре данных, и, следовательно, тем выше способность нейронной сети к обучению.

Литература

А.Ю. Дорогов., А.А. Алексеев. Нейронные сети с ядерной организацией. // Оборонная техника. - 1998. - №7-8. - С.43-46

А.Ю.Дорогов, А.А.Алексеев. Категории ядерных нейронных сетей. //Труды Всерос. науч.-техн. конф.“Нейроинформатика-99” г.Москва 20-22 января 1999г. Сб.науч.тр.Часть 1.- М.: 1999. - С.55-64.

А.Ю.Дорогов, А.А.Алексеев. Быстрые нейронные сети. //Труды международной научно-технической конференции “Пятьдесят лет развития кибернетики”Санкт-Петербург 5-7-октября 1999. - С.120-121.

И.И.Ежов, А.В.Скороход, М.И.Ядренко Элементы комбинаторики. М.: Наука, - 1977. - 80с.

В.Д.Гоппа. Введение в алгебраическую теорию информации. - М.: Наука. Физматлит, - 1995. - 112с.

Site of Information Technologies
Designed by inftech@webservis.ru.