 |
||
ПРИМЕНЕНИЕ НЕЙРОСЕТИ ДЛЯ ИССЛЕДОВАНИЯ ТОНКОСТЕННЫХ КОНСТРУКЦИЙ ДИРИЖАБЛЯ ПРИ ДИНАМИЧЕСКИХ НАГРУЖЕНИЯХ
Е.Г. Евсеев
1, П.Г. Круг2, А.В. Шилин21
Российский государственный технологический университетим. К.Э. Циолковского (МАТИ),
2
Московская государственная академия приборостроения и информатики (МГАПИ)Abstract – The paper examines the research software on the basis of neural network which provides effective simulation of processes arising as a result of impulse load on the surface of cross-sectional closed contour thin-slab curvilinear articles of dirigibles. The results of selecting neural network optimum structure for automated evaluation of liner theory suitability and for calculation of thin-slab structure dynamic conduct are considered.
1. Анализ моделируемых процессов
Применение композитных материалов в тонкостенных элементах конструкций позволяет наиболее полно реализовать их специфические свойства, высокие удельные прочностные характеристики. Наряду с широко распространенными типовыми элементами в виде оболочек вращения, панелей и стержней перспективным представляется использование тонкостенных криволинейных стержней с замкнутым контуром сечения. Большой практический интерес представляют круговые элементы типа тора. Плоские криволинейные рамы встречаются в конструкциях летательных аппаратов и в составе судовых корпусов. При этом, нагрузка часто не лежит в плоскости кривизны таких элементов и характер нагружения не всегда является статическим.
Среди вопросов общей теории тонкостенных стержней [1], рассматриваются задачи статики криволинейных стержней с произвольным жестким контуром: изгиб и кручение плоского стержня с круговой осью малой кривизны, пространственная устойчивость круговых стержней, арок и торообразных оболочек с жестким профилем. Исследования свободных, вынужденных и случайных колебаний пространственно-криволинейных стержней [2] и исследование распространения волн продольных деформаций прямолинейных стержней со сплошным сечением затруднены, так как в литературе практически не имеется решений задач о распространении упругих волн в пространственно криволинейных стержнях.
Таким образом, представляет интерес задача модельного исследования динамических процессов, возникающих в тонкостенных прямолинейных и криволинейных композитных стержнях при импульсном воздействии, в программных средах, способных снизить удельный вес рутинных процедур при оценке эффективности конструкций, а также методов их расчета
[4-6].Пример функционирования исследовательской среды, построенной с использованием нейросетевых технологий, в докладе иллюстрирован при моделировании эффектов, возникающих в результате воздействия импульсной нагрузки в направлении, ортогональном плоскости кривизны композиционных стержней.
2. Структура программной среды
Обобщенная структура программной среды исследования конструкций из композиционных материалов, а также методов расчета этих конструкций (рис.1) включает в себя следующие подсистемы:
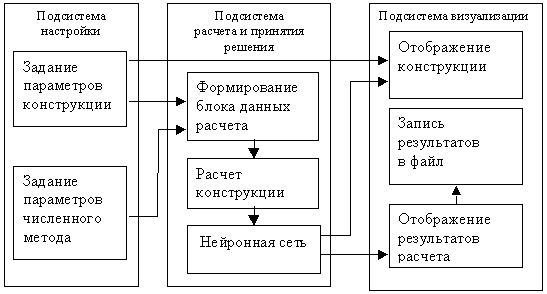
Рис. 1. Обобщенная структура программной среды исследования
3. Типовой алгоритм принятия решений
Ядро программной среды исследования тонкостенных композитных элементов конструкций в режиме импульсного нагружения построено с использованием типовых решений построения САПР (рис 2).
4. Нейронная сеть
Когда нет необходимости, чтобы сеть в явном виде выдавала образец, т.е. когда достаточно, скажем, получать номер образца, ассоциативную память успешно реализует сеть Хэмминга. Данная разновидность нейросети характеризуется (что видно по ее структуре, рис. 3), в сравнении с чаще используемой сетью Хопфилда, снижением затрат на память и также снижением общего объема вычислений.
В основу программной среды исследования, рассматриваемой в докладе, положена нейронная сеть Хемминга, структура которой изображена на рис.3.
Идея данной конфигурации сети моделирования процессов, возникающих в результате воздействия импульсной нагрузки на поверхность тонкостенных криволинейных изделий с замкнутым контуром сечения, состоит в нахождении расстояния Хэмминга от тестируемого образца до всех образцов.
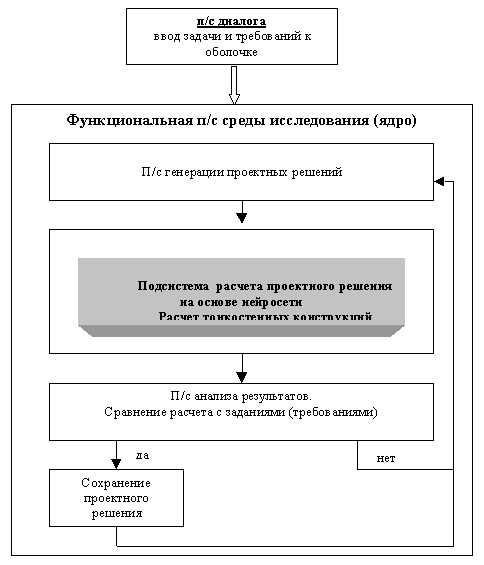
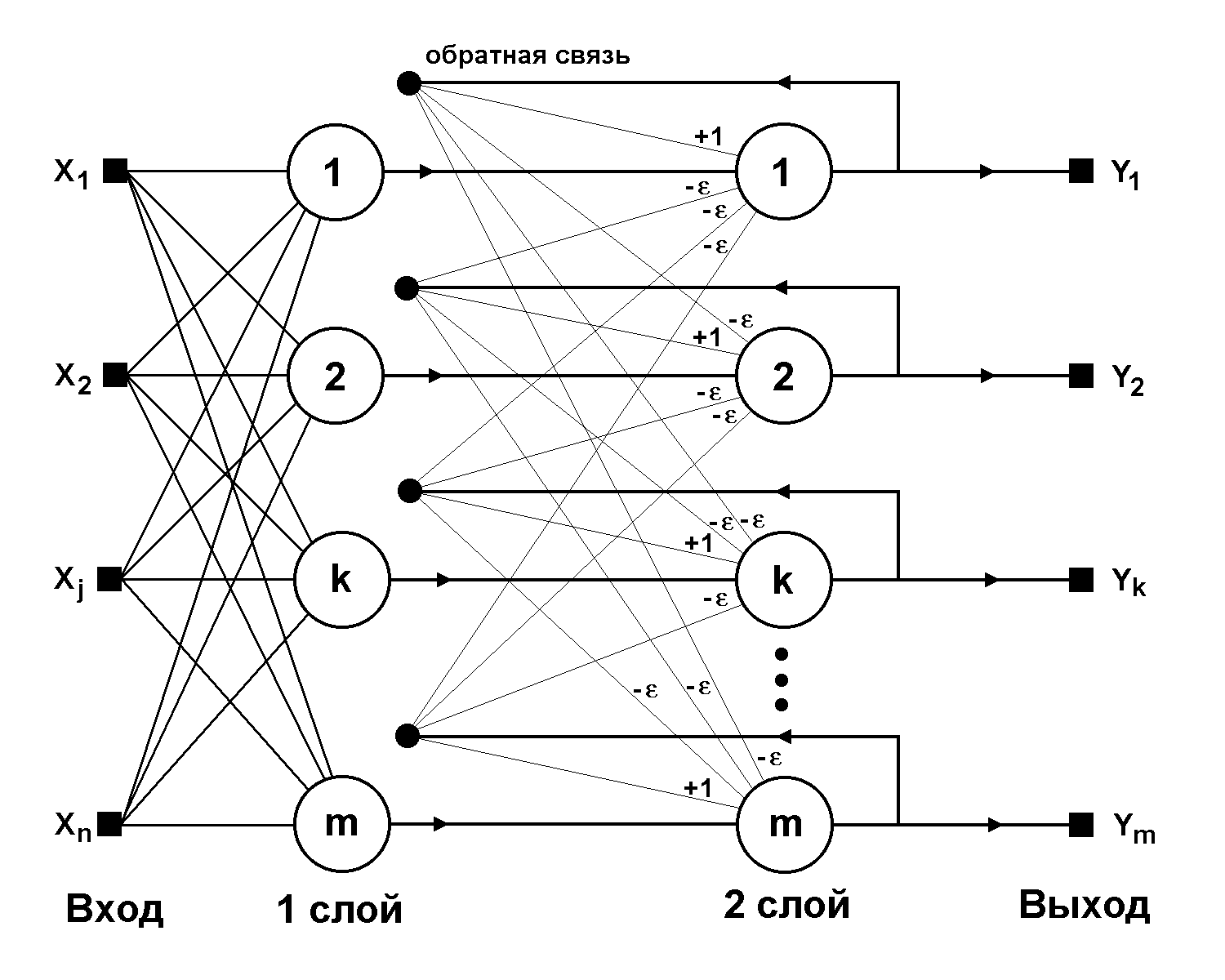
Рис. 3. Структура нейронной сети Хемминга
При этом, расстоянием Хэмминга принято считать число отличающихся битов в двух бинарных векторах. Сеть выбирает образец с минимальным расстоянием Хэмминга до неизвестного входного сигнала, в результате чего будет активизирован только один выход сети, соответствующий этому образцу.
На стадии инициализации весовым коэффициентам первого слоя и порогу активационной функции присваиваются следующие значения:
![]() , i=0...n-1,
k=0...m-1
, i=0...n-1,
k=0...m-1
Tk = n / 2, k = 0...m-1
Здесь
xik – i-ый элемент k-ого образца.
Алгоритм функционирования сети Хэмминга следующий:
1. На входы сети подается неизвестный вектор
X = {xi:i=0...n-1}, исходя из которого рассчитываются состояния нейронов первого слоя (верхний индекс в скобках указывает номер слоя):![]() , j=0...m-1
, j=0...m-1
После этого полученными значениями инициализируются значения аксонов второго слоя:
yj(2) = yj(1), j = 0...m-1
2. Вычислить новые состояния нейронов второго слоя:
![]()
и значения их аксонов:
![]()
Активационная функция f имеет вид порога, причем величина F должна быть достаточно большой, чтобы любые возможные значения аргумента не приводили к насыщению.
3. Проверить, изменились ли выходы нейронов второго слоя за последнюю итерацию. Если да – перейди к шагу 2. Иначе – завершение алгоритма.
При внимательной оценке алгоритма видно, что роль первого слоя весьма условна: воспользовавшись один раз на шаге 1 значениями его весовых коэффициентов, сеть больше не обращается к нему, поэтому первый слой может быть вообще исключен из сети (заменен на матрицу весовых коэффициентов).
5. Пример
В качестве типовой задачи применения программной среды для исследования поведения тонкостенных конструкций при динамических нагружениях, в докладе приводится пример расчета аэрогидроупругости в полной постановке для конструкции дирижабля “АЛА-500” со следующими габаритами: длинна - 224 м., ширина - 110 м (рис. 4).
Рис. 4. Упрощенная модель аппарата типа “АЛА-50”
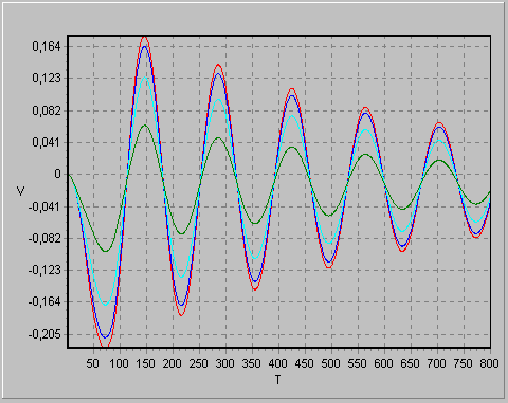 Рис. 5. Типовая реакция
конструкции дирижабля после момента нагружения,
полученная в результате применения программной
среды
Рис. 5. Типовая реакция
конструкции дирижабля после момента нагружения,
полученная в результате применения программной
среды
В ходе модельного эксперимента динамическая нагрузка была приложена по всей оси и действовала в течение времени 0 ?
t ? 800 (рис. 5).Литература
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|