 |
||
THE INVERSE PROBLEM FOR DYNAMICAL MODELS OF GENETIC NETWORKS: FAST COARSE-GRAINED SOLUTIONS BY EVOLUTIONARY COMPUTATIONS
A.V. Spirov, A.B. Kazansky
The Sechenov Institute of Evolutionary Physiology and Biochemistry, Russian Academy of Sciences
Аннотация
– Моделирование кинетики активации генных сетей становится одной из актуальных задач современной вычислительной биологии. Суть проблемы заключается в необходимости решения обратной задачи нахождения параметров системы кинетических уравнений частных производных по имеющимся экспериментальным кривым кинетики активации генов сети. Задачу подбора параметров такой системы уравнений в общем виде решают эвристическими методами оптимизации. В этом сообщении обсуждаются вопросы нахождения параметров средствами генетических алгоритмов и гибридными методами оптимизации.It is increasingly apparent that critical biological processes are under the control of integrated molecular circuits composed of genes. In the last decade, new methods of monitoring gene expression have focused attention on this area by producing exponentially increasing amounts of data. The quantity of this data is reaching and passing the point beyond which it cannot be understood without the aid of new mathematical ideas implemented with modern computing tools. Recent works have shown that it is possible to construct predictive models of the gene networks that control Drosophila segmentation by a method based on large scale computational optimization [Reinitz and Sharp, 1995; 1996]. At present, the range of biological questions that can be investigated with this method are limited by computational capacity. The purpose of the current work is to develop new computational and mathematical tools to push back these limits.
We have elaborated a whole family of new efficient optimization multipurpose methods for analysis of networks of interacting genes, controlling a number of fundamental biological processes. The solving of inverse problem is the kernel of these methods. The procedure reduces to the determination of the parameters of the model (a set of nonlinear ordinary differential equations (ODE's)) by experimentally observed data. The solution - values of parameters is reached by fitting of the trajectories of the equations to the experimental gene expression data and applying least square optimization procedure.
This approach, known as ''gene circuits'', was introduced and developed by Eric Mjolsness, David Sharp and John Reinitz [Mjolsness et al., 1991[. It yields useful biological results, including the correct prediction of certain experimental results when applied to the problem of the formation of the segmental pattern in the fruit fly Drosophila melanogaster [Reinitz and Sharp, 1995; 1996; Kosman et al., 1998].
Methods
Circuit-Based Mathematical Models and Self-Learning IdentificationTechniques. This work is aimed at extension of gene regulation network approach on large-scale gene abundance time-series at coarse-grained level of resolution. The Genetic Regulatory Network approach [Reinitz et al., 1995] has as its starting point a description of the embryonic cell nucleus to be analyzed in terms of primitive objects, having an internal states. Namely, the internal state of a nucleus might be given by specifying the concentrations of a certain set of transcription factors.
Genes are synthetically active and regulate one another: the result is a pattern of regulatory connections between the genes.
Let the interaction of a pair of genes a and b is represent by a single real number Tab of the connection matrix T. There may be many proteins b regulating the gene for protein a and thus influencing the dynamics of a. To make a tractable model, it is assumed that these effects are monotonic in the concentrations and are approximately additive, with nonlinearity confined to sigmoid threshold functions.
Discrete Approach versus a Continuous One. Our aim is to elaborate an effective computational tool for investigation of genetic networks, controlling specific developmental processes in organisms. We tried to reach this aim by perfection of the circuit-based mathematical models, and by developing relevant machine learning identification technique.
The first step in applying of the gene circuit method is to determine the values of Tab and some other parameters. We have got the experimentally observed solutions of gene circuit model, which are gene expression patterns (See Fig. 1). The solutions of these equations depend on both the initial conditions and the values of the parameters of the equations. Our procedure is to fix the initial conditions and seek the set of parameters which minimize the summed squared deviations between the observed data and the solutions of the equations. This procedure is known as a least squares optimization problem. Initially this problem was solved by the method of Simulated Annealing (SA). The advantage of this method is that, under appropriate conditions, it will reliably bring to the global minimum. This advantage is purchased at the cost of intensive computation. In part, this is because a single annealing run requires several million integrations of the equations. Also, because SA is a stochastic method, it is necessary to do repeated fits to ensure that the answer is consistent and reliable.
Recently, Genetic Algorithms (GA) as well as hybrid approach (GA +SA) techniques was applied to this optimization problem [Reinitz, King-Wai Chu, and Deng, 1999]. In this work we try to apply GA technique for discrete versions of genetic circuits approach. Discrete approach implies discrete space of Tab matrix elements. The range of such discrete sets of element values is limited (for example, -128, -64, -32, -16, -8, -4, -2, -1, 1, 2, 4, 8, 16, 32, 64, 128). Mutation, in such a case, is exchange of one of values from this list on another. Advantages of this approach are related with finite set states formed by discrete search manifold. This large but numerable manifold principally allows to look over all points of search space and drastically speed up computations. Weak point of this approach is, of course, coarse-grained level of the search (Cf. Fig. 1 and Fig. 2), while it is tens times faster.
Hybrid Optimizations versus Solo Techniques. The problems that can be attacked by the gene circuit method are currently limited by computational problems. The central idea of this method is the inversion of a dynamical system, consisting of ODE's. Until recently this was reached only by simulated annealing (SA) on a serial processor. On the other hand, sequential and parallel genetic algorithms (GAs) as well as parallel SA have already been used for gene circuit problems solving [Reinitz, King-Wai Chu, and Deng, 1999]. More generally, the solution of these problems lies in the proposed hybrid optimization approach (GA + gradient search). Preliminary results indicate that GA might well be superior for the early part of a search, while gradient search is the best method near the end. This suggests a procedure in which the processors in gradient search are seeded from the optimal population of a GA run.
The Results and Discussion
Three different but related approaches for inferring genetic network structure from expression data were cross-tested.
Classical Gene Circuits Approach to the Model of Drosophila Early Segmentation Genes. The data, described in [Kosman et. al., 1998] were used to obtain a gene circuit which displays a set of regulatory actions which lead to the observed expression patterns of this 4 gap gene system and generation of periodic pattern of expression of even-skipped (eve) gene by aperiodically expressed gap domains (Fig. 1).
Application of the simulated annealing procedure determined a set of parameters for 4 gap + eve equations that gave the closest possible fit to the data [Reinitz and Sharp, 1995]. Several simulated annealing runs gave scores which agreed to within 1%, and nearly identical values for the parameters, so that the results are reproducible and can be reliably taken to represent the global minimum.
Discrete Gene Circuits Approach. We found that discrete computations seems more adequate in case of earlier and transitional patterns of gap genes expression (Fig. 2). This fact is remarkable not only from the methodological point of view but also in its own rights.
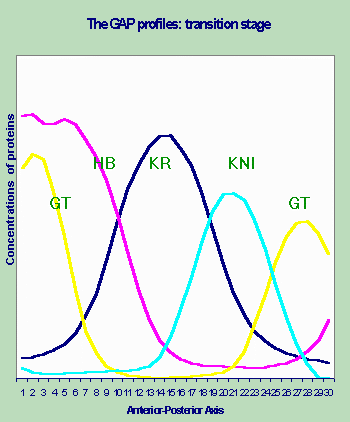
Figure 1. Empirical profiles of the gap genes expression.
Discrete computations are crude enough to simulate refined seven-stripped patterning, being fast and powerful to catch earlier and transitional gap prepatterns. It is evident that tuning imply usage of continuous parameter space.
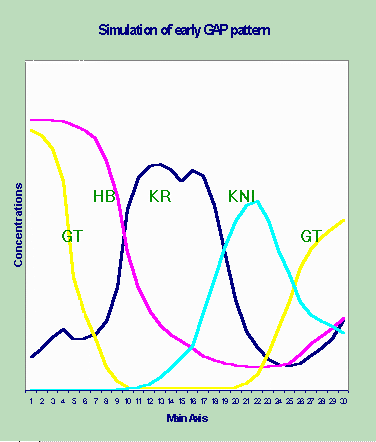
Figure 2. The result of the dynamical modeling.
It is essential that estimated values of Tab matrix elements are close to the results of continuous search. In the devoted table we mark elements similar in sign and value to the results got by Reinitz and Sharp [1995] (Cf. Table).
| Early GAP-profiles governed circuit | |||||
Kr |
hb |
Gt |
Kni |
bcd |
|
Kr |
5 |
-2 |
3 |
-16 |
-32 |
Hb |
-2 |
1 |
14 |
-1 |
42 |
Gt |
-32 |
-2 |
9 |
1 |
9 |
Kni |
-1 |
-64 |
-64 |
-2 |
-4 |
Only five from 20 matrix elements are differ and only two of them differs drastically (diverged matrix elements are stressed).
Hybrid Techniques. The search surface illustrated in the figure 3 is not only rugged, but has grooves. Hence, it is unlikely that gradient search alone, started from random points will lead to a faster solution of the problem. But, application of gradient descent method near the end of a GA-optimization run may add significant efficiency. These methods can shorten execution time by 30 % or more.
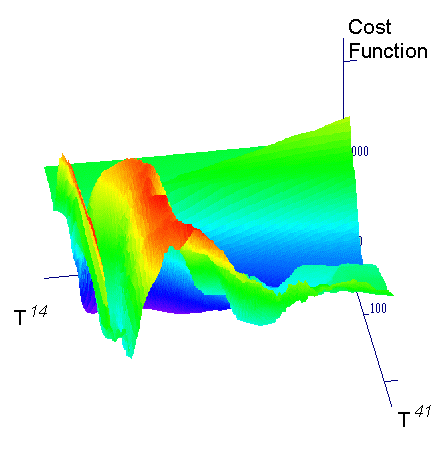
Figure 3. One of the representative crossections through the search space.
Hence GA might well be superior for the early part of a search, and simplex method is the best method near the end. This suggests a procedure in which the processors in a parallel simplex method search are seeded from the optimal population of a GA run. The simplex method then proceeds in parallel until close to frozen.
Conclusions
Our comparative computational tests bring us to conclusions that:
solving of inverse problem for wild-type per se or for unique experimental data give in a result series of network models with very similar expression patterns but with drastically different internal organization;
two-stage strategy for genetic networks deciphering is well effective. At first stage, discrete genetic circuits technique is performed, and at the second - the crude-scale results got on the first stage (elements of the matrix Tab) are refined by means of tuning via classic continuous approach;
Hybrid optimization approach whose key idea is hybrid techniques (genetic algorithms + simplex method) is proposed to speed up the search. GA might well be superior for the early stage of a search, while gradient search is the best method near the end. This suggests a procedure in which the processors in gradient search are seeded up from the optimal population of a GA run.
Acknowledgements
This work is supported by RFBR, grant No 00-04-48515; INTAS, grant No 97-30950; USA National Institutes of Health, grant RO1-RR07801; and CRDF, grant No RB0-685.
References
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|