 |
||
GENERALIZATION OF ARTIFICIAL NEURON
Victor Tolstykh, Irina Tolstykh
St. Petersburg State Technical University.
Polytehnicheskaya 29, St.-Petersburg, 195251, Russia,
e-mail vnt@mail.ru, v_tolstykh@hotmail.com.
Аннотация – Обобщение искусственного нейрона заменой линейной свертки входного вектора с набором весовых коэффициентов на произвольную многопараметрическую функцию. Веса синапсов заменены на набор параметров, которые в данном случае являются не синаптическими коэффициентами, а внутренними параметрами тела нейрона. Обобщен алгоритм обучения обобщенного “
smart” нейрона, позволяющий находить значения произвольного набора параметров, не связанного с размерностью входного вектора. Один “smart” нейрон достаточен для построения нелинейных многомерных зависимостей, ранее требовавших нейронных сетей со сложной топологией. Нейронная сеть является частным случаем “smart” нейрона. Нейронная сеть, состоящая из “smart” нейронов, определяет следующий уровень в иерархической структуре “искусственного интеллекта”.1. Smart Neuron
The artificial neural networks are very popular for purpose of multi-dimensio-nal or complex data approximation. But attention of researches and users is mostly focused in the idea of elaboration and investigation of topology of sophis-ticated neuron networks. In this article we try to generalize the idea of simple single neuron to make one more “smart”.
Single neuron has simple construction. From technical point of view it is only a device for convolution of multi-dimensional vector with constant vector (co-vector) of weights. Mainly focus is in the neuron network topology because the Kholmogorov’s theorem provides a theoretical support of the idea.
Accordingly the theorem, we can make decomposition of any differentiable multidimensional function into the one-dimensional set of simple functions-neurons. It was very exciting idea and the realization of it gets us important applications. From mathematical point of view any network can be represent as a set of linear independent functions with free parameters-weights. Therefore, good making network is only subset of parameterized functions, which can approximate wide class of data.
From this it is obviously that a linear parameters-weights entry is very rigorous limitation. Alternative of this is making the network with more complex elements than only simplest artificial neurons. We named the neuron “Smart” Neuron, because this single neuron can approximate a multi-dimensional non-linear dependence instead the regular neuron, which can approximate only linear dependence. Thus it is a generalized idea of simple artificial neuron.
Using smart neurons we can make more powerful existing ordinal neural networks just only replacing original neurons by smart ones.
Definition. Smart Neuron (SN) is a device, which calculates value of multi-dimensional non-linear function.
The model of SN is any multi-parametric set of analytical differential functions.
No weights vector in the definition is required. The training process only interactively determines free coefficients of model inside the neuron.
2. Training algorithm
Theorem. Let ![]() be a
differentiable by all parameters
be a
differentiable by all parameters ![]() function
of n variables
function
of n variables ![]() . Let
. Let ![]() is unlimited training set. Then we can define
parameters of the function iteratively using training process
is unlimited training set. Then we can define
parameters of the function iteratively using training process
![]() ,
,
where a is a small positive constant.
Initial value of W is arbitrary. In particular case if n=m and ![]() then formula (1) has conventional form [1,3]
then formula (1) has conventional form [1,3]
![]()
Accordingly to the definition we can choose any set of functions whatever we want. The only approximate property is important. Here we have for example set of polynomial, rational functions, trigonometric functions and others. Even linear combination of neurons can be used. Thus SM can be conventional neuron sub-network also.
Dualism of SM: We can consider SN as a generalization of conventional neuron and as a generalization of whole network in the same time. It is good point for evaluation of hierarchical structure of future networks with the intelligence increasing. Anyway the combination of smart neurons in regular network seems to be optimal.
3. Using with Neural Network
The interpretation of conventional artificial neural networks can be as follow:
Let m is a number of elements on the input layer – dimension of input vector,
ni is a number of neurons on the ith hidden layer, n is a number of elements on the output layer – dimension of output vector.
We can interpret the scheme in term of multi-dimensional mappings
![]() ,
,
where every mapping gk is a transformation of input vector from layer k-1 to layer k.
Superposition ![]() is the
multi-dimensional vector-function we are looking for. Every local function
is the
multi-dimensional vector-function we are looking for. Every local function ![]() is a superposition of linear function
is a superposition of linear function ![]() with free parameters W and non-linear
predefined function
with free parameters W and non-linear
predefined function ![]() .
. ![]() is a scalar product (convolution) between
input vector and weight vector, which is internal for every neuron. In term of
interconnection of W and V we will name the neuron “linear neuron”.
Certainly the generalization of idea of simple linear neuron is a free parameterized
function
is a scalar product (convolution) between
input vector and weight vector, which is internal for every neuron. In term of
interconnection of W and V we will name the neuron “linear neuron”.
Certainly the generalization of idea of simple linear neuron is a free parameterized
function ![]() .
.
This makes some difference between generalized artificial neuron and the biological neuron, because there are no weights in synapses and number of parameters does not depend from dimension of input space.
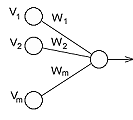
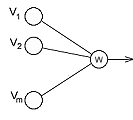
Fig.1. Conventional and Smart Neurons
Number of parameters and its interconnection with input vector is
arbitrary and makes its purpose the better approximation of gk. That’s
why we name the neuron “Smart”. Ordinary neuron can approximate the linear dependence
if the area bounded by non-linear function ![]() .
In contrary the SN can approximate any non-linear dependence if the internal model of SN
generates a basis functions class.
.
In contrary the SN can approximate any non-linear dependence if the internal model of SN
generates a basis functions class.
4. Usage
Example: the polynomial is a basis for any infinite differentiable function on the bounded area. Generally we can use for this purpose the class of differential linear equation solutions. Class of rational functions includes the polynomial class and also generates basis function class for any differentiable function.
The whole network is represented by multi-dimensional vector-function ![]() . It is also a function with a set of free
parameters of every neuron
. It is also a function with a set of free
parameters of every neuron ![]() , where W
is a summarized vector of all weights in the network. Of course the network can be also
generalized as a one smart neuron.
, where W
is a summarized vector of all weights in the network. Of course the network can be also
generalized as a one smart neuron.
In this point of view the main problem is how to enhance the training process for purposes of SN training. Obviously conventional back-propagation algorithm does not convenient.
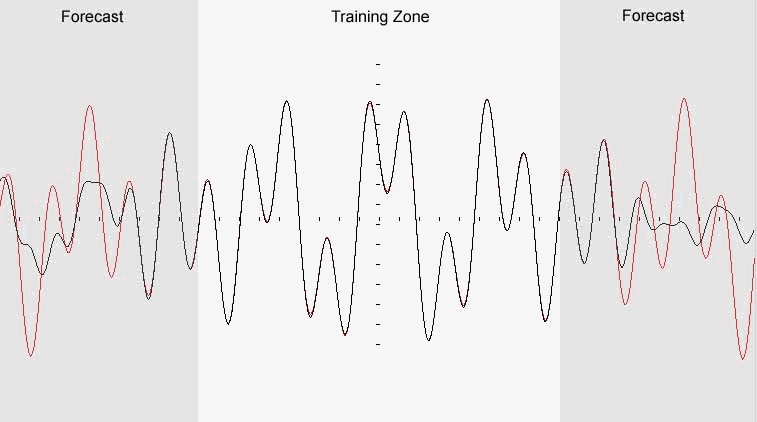
Fig.2.Quasi-periodic function restoration
Example. Quasi-periodic function is a linear combination of periodic functions. We can approximate that sort of function by periodic using Fourier series.
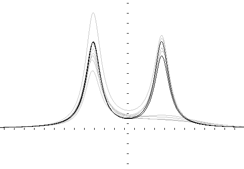
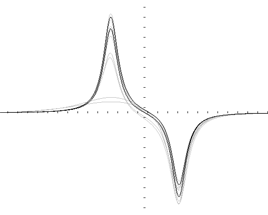
Fig.3. Rational functions restoration
Example. The double peaks signals and several steps of their restoring by using only one neuron with internal function as a rational polynomial of the 4th power.
Usage Neural Network model as single Smart Neuron. In this case general formula does not exist. The main idea of neural network is in the simple linear decomposition of multidimensional function by a set of simple neurons:
![]() .
.
These neurons are linear functions in the finite areas. For example it could be wavelet decomposition
![]() ,
,
where y i(x) is a
wavelet function ![]() so-called “inverse of
Mexican hat”.
so-called “inverse of
Mexican hat”.
Conventional neural network using “inverse of Mexican hat” is a powerful method for approximation of multi-dimensional dependences. But the only linear coefficients of “hats” in the formula are free. It is an excessive limitation. Using this way we need a lot of neurons even for simple dependence. Another trouble of flexibility we get from the model, because the result usually is a “black box”.
On the other hand the Smart Neuron allows use the models with arbitrary coefficients entry and it proves that this method includes all previous methods with a particular case as parameter-weight.
Conclusion
The neural network is a particular case of “smart” neuron. We can construct next level of hierarchy of neural networks using the set of generalized “smart” neurons in the network. It allows us to increase the “intellect” of artificial neural networks.
References
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|