Н.Г. Ярушкина, А.М. Наместников

Ульяновский государственный технический университет

На практике довольно часто приходится решать задачу размещения разногабаритных электрорадиоэлементов (ЭРЭ) на непрерывном монтажном пространстве. Структура задачи размещения разногабаритных элементов задается посредством ограничений пространства размещения (габариты конкретного корпуса или монтажной платы), элементы размещения, заданные своими габаритами. Принципиального отличия в такого рода задачах между объемным и пространственным размещением не существует (трансформация задачи в трехмерный вид осуществляется путем доопределения ограничений по третьей координате и выбор числа уровней размещения и их ориентации). Каждый элемент, предназначенный для размещения представляется установочной площадью, которая задается двумя параметрами: длиной и шириной.

Данная задача, относящаяся к классу оптимизационных задач, может быть решена с использованием генетических алгоритмов[1]. Обобщенная схема стандартного генетического алгоритма следующая:

while(not done(termination_condition); пока не завершена эволюция

Характерной особенностью использования стандартного генетического алгоритма для решения практических задач является необходимость уточнения его параметров. При создании программной реализации генетического алгоритма размещения разногабаритных ЭРЭ были выполнены следующие модификации:

В результате проведенных исследований поведения генетического алгоритма были анализированы следующие схемы отбора [1, 2]: пропорциональный отбор, линейное ранжирование и равномерное ранжирование. Результаты однозначно показали эффективность схемы пропорционального отбора при решении задачи размещения методом генетического алгоритма в отличии от остальных схем отбора. Однако для предотвращения перехода к простому случайному выбору (все хромосомы, отбираемые в пул родителей, имеют примерно одинаковые значения функции оптимальности) перед отбором значения функции оптимальности всех хромосом подвергаются масштабированию. При исключении такой операции процесс сходимости функции оптимальности переходит в хаотический режим.

Результаты анализа поведения генетического алгоритма в зависимости от значений вероятности мутации приведены на рис. 1. Эксперимент проводился для значений вероятностей мутации в диапазоне от 0.1 до 0.6 с шагом 0.1. Значения вероятности более 0.6 не приводят к сходимости функции оптимальности генетического алгоритма за приемлимое время.

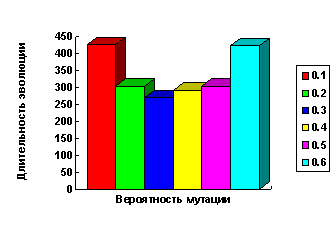
Рис.1 Зависимость длительности эволюции от вероятности мутации

В соответствии с результатами, представленными на рис.1, в качестве оптимальных значений вероятностей мутации выбирают значения из отрезка [0.3, 0.4].

Кроме стандартного генетического алгоритма было проведено исследование ряда эволюционных стратегий. Одной из них была стратегия “только мутация” с пропорциональным оператором селекции, функцией оптимальности, выражаемой формулой (1). Результаты одного из экспериментов с данной стратегией показаны на рис.2, где можно отметить абсолютную хаотичность процесса и, как следствие, неприменимость рассматриваемой стратегии для решения задачи размещения ЭРЭ методом генетического алгоритма.

Рис. 2 График функции оптимальности при эволюционной стратегии “только мутация”

На рис. 3 показаны в сравнении вид графиков функции оптимальности генетического алгоритма с альтернативной стратегией (а) и стандартного генетического алгоритма с оператором рекомбинации в виде одноточечного кроссинговера (б).

Ряд экспериментов с алгоритмом, применяющим стратегию с альтернативным оператором рекомбинации показал выявил особую результативность оператора рекомбинации (3,3), хотя в целом результаты, показанные данным видом алгоритма хуже, чем в случае со стандартным генетическим алгоритмом с одноточечным кроссинговером. В первую очередь это связано с тем, что значительное увеличение точек разреза хромосом ведет к разрушению хороших подобластей потенциальных решений. На рис. 3 это заметно по многочисленным “всплескам” на графике.

б) одноточечный кроссинговер

Рис.3 Графики функций оптимальности генетического алгоритма

Кроме исследований поведения стандартного генетического алгоритма в зависимости от его параметров были проведены эксперименты с так называемым “мобильным алгоритмом”. Его основные отличия от стандартного генетического алгоритма следующие [1]:

• использование хромосом переменной длины, которые могут быть либо пере- либо недоопределены по отношению к решаемой задаче;
• введение правил чтения или экспрессии генов;
• использование операторов CUT (разрезание) и SPLICE (сцепления) вместо традиционной схемы кроссинговера;
• конкуренция между строительными блоками генотипа для отбора оптимальных;
• деление эволюции на две фазы: предварительная фаза и фаза процессинга.

Результаты экспериментов с данным алгоритмом показали его неэффективность для решения задач размещения. Сходимости функции оптимальности не наблюдалось, а вид графика функции оптимальности был практически идентичен графику на рис. 2. На наш взгляд, такое положение дел связано с особенностью решаемой проблемы, поскольку по части потенциального решения в данном случае нельзя однозначно сказать, будет ли полное решение эффективным или нет. Следовательно, возникает проблема отбора оптимальных строительных блоков [1].

Таким образом, результативное решение задачи размещения разногабаритных элементов на непрерывном монтажном пространстве может быть найдено с использованием генетических алгоритмов. Предложенные методы кодирования решений и функция оптимальности способствуют эффективному поиску решения задачи размещения.

В настоящее время с целью обеспечения более быстрой сходимости функции оптимальности генетического алгоритма к оптимуму решается задача включения в цикл эволюции нечеткого контроллера параметров алгоритма. Анализ многочисленных графиков функции оптимальности позволил выявить некоторые эвристики, которые предполагается использовать в БЗ контроллера.

Программный продукт, на основе которого проводились эксперименты, написан на языке Visual C++, и функционирует под управлением операционных систем Windows 95/NT.