Современные научные и практические задачи определения характеристик и состояний сложных технических и природных объектов, процессов и систем, динамика их развития, прогнозирования и контроля их свойств, а также управления ими или принятия оптимальных уп

интеграция разнотипной информации в системах поддержки принятия решений с метрологическим обоснованием получаемых результатов на основе Байесовских интегрирующих технологий

С.И. Крамарь, О.Г. Иванов

Санкт-Петербургский государственный электротехнический университет “ЛЭТИ” им.В.И.Ульянова (Ленина)

Abstract — This paper is devoted to the problems of the integration of incomplete unaccuracy and which are represented information in the variant forms. The main Methodologies is the Regularizing Bayesian Approach (RBA), the Information Technologies of Bayesian Intelligent Measurement (IT BIM) and Bayesian Integrant Technologies.

Байесовские интеллектуальные измерения (БИИ) и интегрирующие свойства регуляризирующего байесовского подхода являются основой для разработки информационных технологий интеграции информации с контролем качества принимаемых решений. Основным препятствием для применения РБП в данном направлении до настоящего времени были неустойчивость и чувствительность байесовских оптимальных оценок при неполной, неточной и нечеткой информации. Но последние модификации байесовского подхода направлены на получение устойчивых решений в условиях значительной неопределенности.

Интеграция разнотипных информационных потоков с метрологическим обоснованием получаемых решений может проводится на специальном типе шкал- шкалах БИИ в соответствии с формой представления и степенью неопределенности полученной информации. При этом числовые данные измерений и пр. могут быть проинтегрированы с лингвистическими экспертными оценками на математической основе.

Интегральный поток данных может быть представлен следующим образом [2]: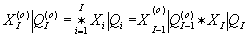

(1)

где -поток данных i-го типа, состоящий из J элементов x_ij, - полученных при условиях , включающих априорную информацию об информационных потоках, метрологические требования к ним, ограничения и допущения при их формировании.

В зависимости от самого источника информации имеется возможность получения информационных потоков нескольких различных типов:

?eneiaie eioi?iaoee (aaiiua oaoie?aneeo ecia?aiee, aaiiua noaoenoe?aneie io?aoiinoe e a?oaea aicii?iua aaiiua, i?aanoaaeaiiua a aeaa eiee?anoaaiiie ioaiee ia?aiao?a eee naienoaa iauaeoa, o.a. ?eneiaiai cia?aiey);

eeiaaenoe?aneie eioi?iaoee (aaiiua yenia?oiuo ciaiee a aeaa yenia?oiuo ioaiie, aaiiua oaenoiauo iienaiee (eioi?iaoey, eioi?ay eiaao iainii?eio? aa?iinou i?e aiaeeca ninoiyiey iauaeoa, ii ii?ao auou eioa?i?aoe?iaaia oieuei a oeacaiiie oi?ia — iai?eia?, oaiieiae?aneee eaeaiaa?u aey yeinenoaiu caiiaaaieea eee ianoa ia?anoeeeu oaiiuo aeaia ?ua aey ioaiee ninoiyiey iiioeyoee));

aiaeeoe?aneie eioi?iaoee (ciaiey a aeaa ooieoee e caaeneiinoae);

naiaioe?aneie eioi?iaoee (ciaiey a aeaa i?aaee);

a?aoe?aneie eioi?iaoee (aaiiua ay?i- e einie?aneie nuaiee, iacaiiiai oioia?aoe?iaaiey, aaiiua aiaeeoe?aneeo ea?o, a?aoeeia e aeaa?aii);

aoaei e aeaai eioi?iaoee (oeeuiu, eeeiu e o.a.)

Свертка информации о значении элемента x_ij, i=1,…I производится по модифицированной формуле Байеса [2]: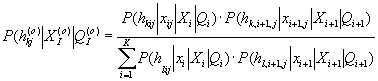

(2)

где h_kj^(o) – интегральная (для совокупности потоков информации X_I^(o)) регуляризирующая байесовская оценка (РБО); h_kij – РБО для X_i потока данных.

Метрологическое обоснование каждого типа информационных потоков ведется в соответствии с методической базой метрологии БИИ и принципами преобразования комплексов метрологических характеристик, которые включают показатели точности, надежности (уровней ошибок 1 и 2 рода) и байесовской достоверности для каждой РБО.

Свертка комплексов метрологических характеристик {MX}_kij РБО h_kij выполняется в соответствии со следующим выражением [2]: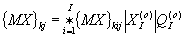

(3)

Для интеграции лингвистических РБО h_kij^{(l )} в интегрирующих технологиях применяется модифицированная формула Байеса для свертки функций принадлежности [2]. Интеграции вероятностной и возможностной информации производится на основании методологии РБП и БИИ в виде сопряженной регуляризированной байесовской оценки в соответствии с формулой[2]:

h^(ou)=h_kj^(ol )* h_kj^(o) (4)

Методологическая основа свертки такого рода рассмотрена в известной литературе.[1,2,3]

Алгоритм интеграции разнотипной информации на основе Байесовских интегрирующих технологий, являющихся новой модификацией РБП и БИИ, можно представить как алгоритм обработки информации на шкалах БИИ. На шкале БИИ с каждым элементом носителя шкалы h_k связывается сложная структура, включающая в себя условную плотность вероятности получения измерения или оценки x в случае верности гипотезы h_k f(x|h_k) и вероятность данной гипотезы. Интерпретация данной вероятности как априорной или апостериорной зависит от этапа, на котором она рассматривается.

При этом при раздельном рассмотрении та часть шкалы, которая содержит функции f(x|h_k) называется текущей шкалой, а та, которая содержит вероятности гипотезы - априорно-апостериорной шкалой.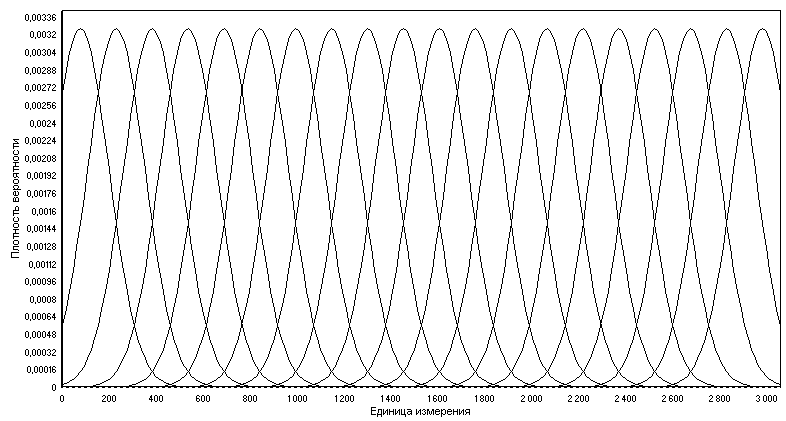

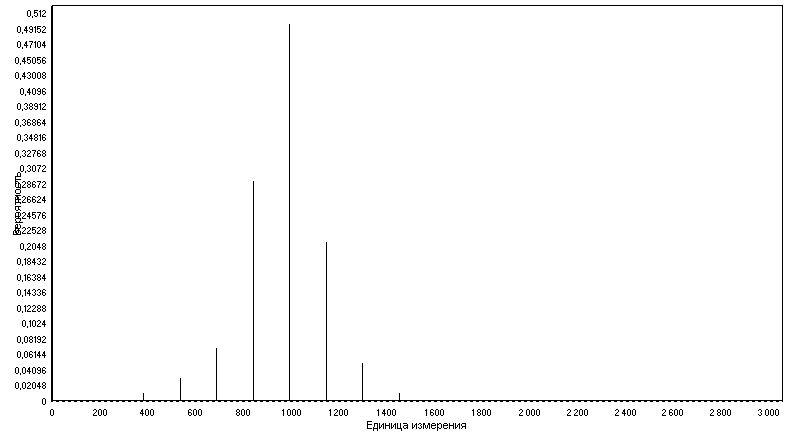
Рис. 1. Структура числовой шкалы БИИ

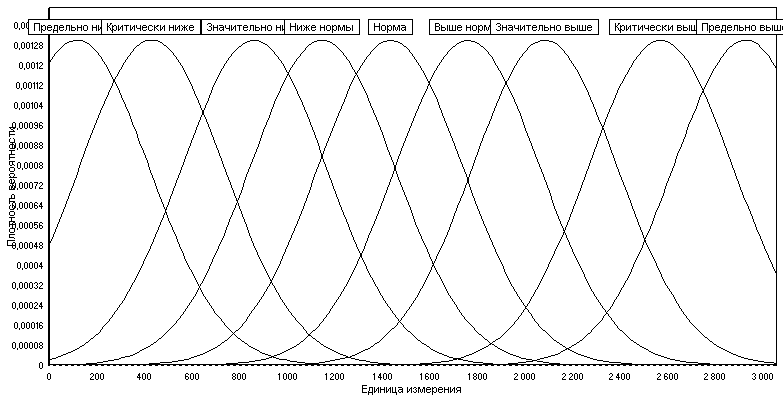
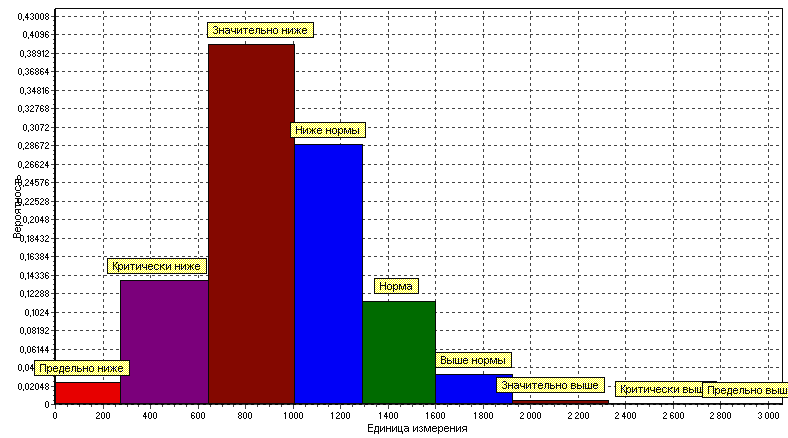
Рис. 2. Структура лингвистической шкалы БИИ

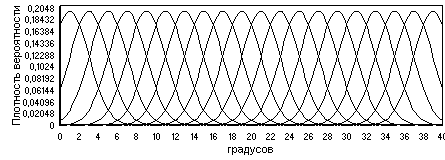
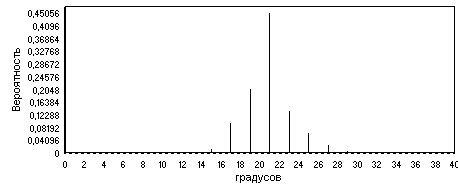
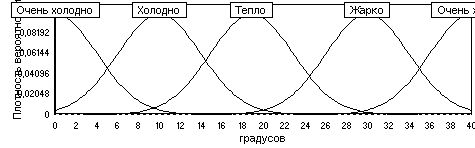
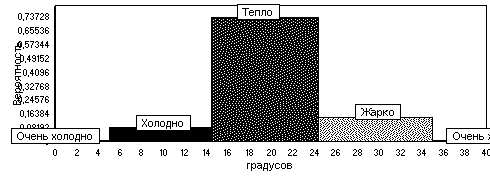
Рис. 3. Сопряженные числовая и лингвистическая шкалы БИИ

При переходе от числовых шкал к лингвистическим используется формула

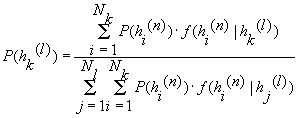(5)

где P(h_k⁽ⁿ⁾) - вероятность k-й гипотезы на числовой шкале,

P(h_i^(l)) - вероятность i-й гипотезы на лингвистической шкале

f(h_k⁽ⁿ⁾| h_i^(l)) - значение условной плотности вероятности получения оценки параметра X при верности гипотезы h_i^(l)

При переходе от лингвистических шкал к числовым используется формула

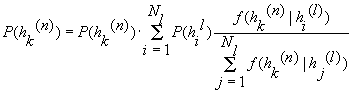(6)

где P(h_k⁽ⁿ⁾) - вероятность k-й гипотезы на числовой шкале,

P(h_i^(l)) - вероятность i-й гипотезы на лингвистической шкале

В результате обработки информации на шкалах БИИ (интеграции числовой и лингвистической информации) получается множество решений с различными значениями точности, надежности и достоверности значащих гипотез.

Для оценки качества решений, полученных на шкалах БИИ, необходимо создать комплекс метрологических характеристик (КМХ), позволяющий получать такие оценки в виде количественных показателей. В КМХ включаются показатели точности, надежности и достоверности решений.

(7)

Показатель для оценки точности должен базироваться на систематической погрешности, определяемой расстоянием между соседними элементами носителя шкалы p(h_s,h_s+1). При равномерной шкале эта величина будет постоянной, при неравномерной эта составляющая равна максимальному расстоянию между соседними элементами носителя шкалы:

(8)

Наиболее удобной формой представления показателя точности является приведенная систематическая погрешность:

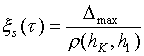, (9)

где - абсолютная погрешность, равная максимальному расстоянию между соседними элементами носителя шкалы

- диапазон шкалы .

В окончательной форме выражение для точности может быть записано следующим образом:

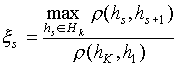(10)

Надежность результата БИИ характеризует устойчивость решения. Показатель надежности основан на уровнях ошибки первого и второго рода и определяется как

(11)

где - уровень ошибок первого рода (отражающий вероятность отвержения правильного решения на шкале);

- уровень ошибок второго рода (характеризующий вероятность принятия неправильного решения шкале).

Уровень ошибок первого и второго рода на шкале выбирается как максимальные из всех вероятностей ошибок первого и второго рода гипотез шкалы. Вероятности ошибок первого и второго рода для гипотез шкалы вычисляются следующим образом:

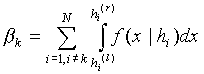
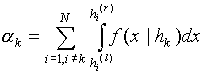
(12)

(13)

где f(x|h) - условная плотность вероятности поступления значения x при условии верности гипотезы h

h_i^(r) - правая разделяющая байесовская граница для i-й гипотезы

(14)

h_i^(l) - левая разделяющая байесовская граница для i-й гипотезы

(15)

Показателем достоверности каждой гипотезы на шкале служит апостериорная вероятность его появления, определяемая по формуле Байеса. Достоверность самой шкалы при этом принимается сумме достоверности гипотез и соответственно равна 1. Однако во многих случаях из практических соображений с целью удаления малозначащих гипотез на шкале оставляют только набор гипотез, удовлетворяющих некоторому критерию значимости. В таком случае достоверность шкалы определяется как:

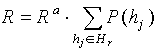(16)

где R - окончательная достоверность решения на шкале

R^a- достоверность шкалы до удаления не значимых гипотез

H_r. - множество значимых гипотез на шкале

Таким образом, любая операция обработки данных на шкалах БИИ должна поддерживать описанный выше комплекс метрологических характеристик - точность, надежность и достоверность.

Схема алгоритма интеграции информации представленана рис.4

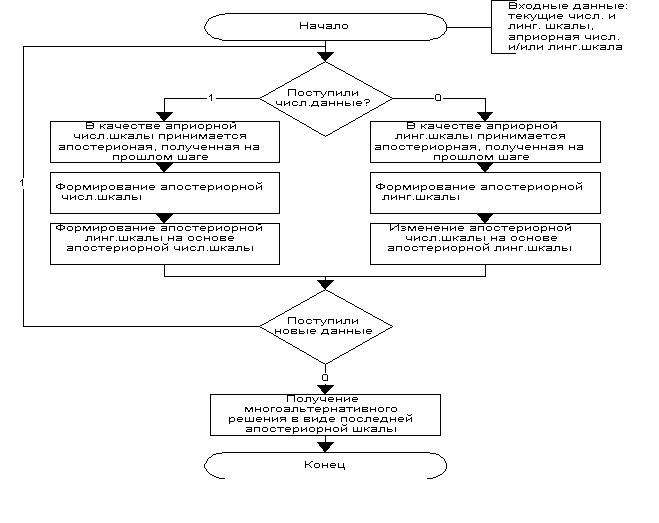Рис. 4. Алгоритм интеграции разнотипной информации

Литература

Недосекин Д.Д., Прокопчина С.В. Информационные технологии интеллектуализации измерительных процессов. - СПб, Энергоатомиздат, 1995, 185 с

Прокопчина С.В. Байесовские интегрирующие технологии на основе интеллектуальных и мягкихизмерений//Сборник докладов конференции SCM’99. - СПб: СПбГЭТУ, 1999 – с.25-32

Прокопчина С.В. Разработка методов и средств байесовской интеллектуализации измерений взадачах мониторинга сложных объектов / Дисс. на соиск. уч. ст. докт. техн. наук –Спб.; ЛЭТИ, 1995. – 405с.

Крамарь С.И. Информационнаятехнология сбора,интеграции иконтроля качества экологической информациина основе байесовских интеллектуальных измерений (БИИ) //Сборник докладов конференции SCM’99. - СПб: СПбГЭТУ, 1999 – с.25-32

Иванова-Разумова А.В., Иванов О.Г., Бровчак С.В. Регуляризирующий байесовский подход (РБП) при выборе стратегий оптимального природопользования//Сборник докладов конференции SCM’99. - СПб: СПбГЭТУ, 1999 – с.184-185

Прокопчина С.В. Экспертная система интеллектуальных измерений "АССИСТЕНТ", "Измерительная техника", 1992, N 8.

Прокопчина С.В. и другие. Экспертные системы на основе регуляризирующего подхода для экосистемного мониторинга // Идентификация, измерение зависимостей и интеллектуальные системы, 1993.

Ивченко Б.П. Мартыщенко Л.А. Монастырский М.Л. Теоретические основы информационно-статистического анализа сложных систем. - СПб: Лань, 1997 – 320с

Site of Information Technologies
Designed by inftech@webservis.ru.