Сайт Информационных Технологий

МЯГКОЕ ОБНАРУЖЕНИЕ СИГНАЛОВ В ЗАШУМЛЕННЫХ ДИСКРЕТНЫХ ИЗМЕРЕНИЯХ

В.М. Бахилин

Санкт-Петербургский Научно-исследовательский институт уха, горла, носа и речи

Abstract – A new method of signals detection in corrupted with noise discrete measurements proposed. It is supposed, that the signals have the characteristic form, the verbal classification of signals is a priori performed, and each class is presented by the image of a nominal signal. The piecewiese linear approximation of nominal images, procedure of recognition of the ordered sequence of linear elements and decisive rule of reference of the found sequence to one of classes is supposed. The algorithm of detection of a visually distinguishable linear element on a background of measuring noise is advanced. An example of computer analysis of nystagmic eye movement is presented.

1. Введение

Методы фильтрации, позволяющие отделить полезный сигнал от измерительных шумов, как правило, строятся в предположении, что на полезный сигнал наложена аддитивная помеха и измеряется суммарный сигнал. Если спектры полезного сигнала и шума накладываются друг на друга, то для выделения сигнала используются статистические методы оценивания (см. [1,2] и ссылки в них). Первым фильтром, минимизирующим воздействия помех, был фильтр Винера, основанный на методе наименьших квадратов. В 1960 г. Калман предложил рекурсивный метод фильтрации, в котором применяются параметрические модели полезного сигнала и помех. Фильтр Калмана использует линейные модели процессов. Однако, во многих практически важных задачах полезный сигнал существенно нелинеен. Появились различные варианты нелинейных фильтров Калмана. Появились и новые идеи фильтрации, основанные на использовании порядковых статистик [3]. Недостатком последних методов является большой объем вычислений, связанных с упорядочением длинных выборок.

В настоящей работе рассматривается частный случай задачи фильтрации, когда полезный сигнал имеет характерную, хотя не строго определенную форму. Такие задачи часто встречаются в медицине при обработке кардиограмм, энцефалограмм и т.д., в сейсмологии, геофизике и других науках. В технических задачах поиска дефектов возможны случаи, когда дефект приводит к появлению в измерительных процессах сигналов характерной формы, по которой специалист безошибочно идентифицирует дефект.

В работе предлагается метод автоматического выделения полезного сигнала, основанный на построении нечеткого образа полезного сигнала и его распознавании с помощью заранее сформированных функций принадлежности. Отличительной особенностью задачи распознавания сигнала от более общих задач распознавания образов является возможность представления сигнала на двумерной плоскости в виде однозначной функции времени. Это позволяет аппроксимировать любой сигнал последовательностью элементарных (например, линейных) функций, заданных на последовательных отрезках аргумента. Достоинством метода является простота вычислительных алгоритмов, небольшой объем требуемой компьютерной памяти и высокая скорость обработки даже на ЦВМ предшествующих поколений.

Метод и реализующие его алгоритмы иллюстрируются примером обработки записи окулограммы с выделением нистагма.

  1. Постановка задачи

Предполагается, что характерные формы сигналов известны априори и проведена вербальная классификация сигналов. Каждый класс представлен изображением номинального сигнала, причем допустимо изменение масштаба номинального образа по вертикали и (или) по горизонтали и при масштабировании сохраняется различие между номинальными образами различных классов.

Требуется в зашумленном измерительном процессе опознать фрагменты записи, содержащие сигналы, которые могут быть отнесены к одному из вербальных классов.

3. Метод обнаружения сигналов

Формализация поставленной задачи включает следующие этапы:

  1. преобразование вербальной классификации в формальную;
  2. представление формальных номинальных представителей классов в виде последовательности легко распознаваемых элементов;
  3. построение решающего правила, относящего к одному из классов последовательность опознанных элементов;
  4. построение алгоритма распознавания элемента образа.

Наиболее удобным и простым способом преобразования вербальной классификации в формальную представляется кусочно-линейная аппроксимация изображений номинальных сигналов, сохраняющая различия между представителями различных классов. Будем называть кусочно-линейную аппроксимацию изображения номинального сигнала формализованным номинальным образом (ФНО) сигнала.

Представим ФНО в виде упорядоченной совокупности линейных функций. Если обозначить Ai ФНО сигнала i-того класса, то

,

где aij - j-тый линейный элемент образа Ai , k - количество распознаваемых классов, ni - число линейных участков в кусочно-линейной аппроксимации образа Ai .

Каждый элемент aij ФНО характеризуется двумя параметрами: длительностью Tij и углом наклона a ij : aij =f (Tij , a ij ) . Тогда i-тый ФНО может быть представлен как функция упорядоченного множества пар

Изменение масштаба образа приводит к одновременному изменению всех Tij , jI {1,n}, в kT раз и (или) всех aij в ka раз с автоматическим смещением граничных точек элементов до совпадения начала следующего элемента с концом предыдущего. Будем считать, что образ

совпадает с образом Ai , если существуют такие kT и ka , что выполняются равенства

(kTTij , ka a ij ) = для всех jI {1, ni}.

Для определения решающего правила следует построить функции принадлежности, характеризующие расстояния между анализируемым сигналом и ФНО. Ясно, что расстояние зависит от числа линейных элементов, их порядка и параметров. Если расстояние между исследуемым сигналом и одним из ФНО не превышает заданного порогового значения, то сигнал считается обнаруженным и принадлежащим классу, представленному соответствующим ФНО.

4. Алгоритм распознавания линейного элемента

Выберем в подлежащей обработке записи визуально различимые линейные элементы минимальной длительности Tm и с минимальным углом наклона a m. Пусть D Ti:=[ti - Tm , ti] - отрезок времени с началом в точке ti - Tm и длительностью Tm . Точке ti поставим в соответствие среднее изменение ординаты за время Tm :

D hi(ti) := (y(ti)- y(ti - Tm))/Tm ,

и определим функцию j (ti)

.

Ясно, что при отсутствии измерительного шума на участке линейного элемента мы получим подряд m единичных значений j (ti), j (ti+1),...,j (ti+m). При наличии измерительного шума такой результат не получить. Поэтому построим функцию принадлежности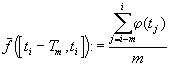

.

Такая функция принимает единичное значение на линейном элементе любого ФНО при отсутствии измерительных помех и нулевое значение на участках с углом наклона меньшим угла наклона самого пологого линейного элемента всех ФНО. В условиях измерительных шумов значения принадлежат интервалу [0,1]. Поэтому для принятия решения о наличии линейного элемента на обрабатываемом участке записи следует задаться некоторым пороговым значением функции принадлежности . Будем считать, что интервал [ti , ti+ Tm] содержит линейный элемент некоторого образа, если ? .

После опознания линейного участка производится поиск полного линейного элемента и оценка его параметров. Эта процедура включает следующие шаги.

  1. Пусть обнаружено, что отрезок [ti,ti+Tm] принадлежит линейному элементу. Тогда анализируются прилежащие отрезки [ti+Tm , ti+2Tm] , [ti+2Tm , ti+3Tm] и т.д. до тех пор пока на участке длительностью Tm функция принадлежности не примет значение, меньшее .
  2. Абсциссой начальной точки считается ti, ординатой - x(ti) - среднее значение измерений на отрезке [ti- Tm , ti].
  3. Вычисление координат конечной точки линейного элемента. Пусть отрезок [tk,tk+Tm] - первый, на котором функция принадлежности приняла значение fk < . Тогда концом элемента считается точка с абсциссой tK = tk+ Tm ? fk ? . За ординату xK принимается среднее значение измерений на участке [tk+ Tm ? fk ? , tk+ Tm] .
  4. Параметры обнаруженного линейного элемента вычисляются по формулам: T = tk- ti , a = arctg((xk- xi)/(tk- ti)).

5. Пример. Обнаружение нистагма

в зашумленной записи окулограммы.

Нистагм представляет собой серию ритмических глазных движений, включающих медленное (компенсаторное) отклонение глаза в одном направлении и последующий быстрый его возврат в исходную позицию (саккада). Различные виды патологического нистагма сопровождают заболевания центральной нервной системы, внутреннего уха, зрительной системы. Нистагменная диагностика приобретает возрастающее значение в медицинской практике. Во время обследования пациента в память компьютера записываются кожные потенциалы с электродов, закрепленных на глазных мышцах (окулограмма). Нестабильность кожных потенциалов, зависящих от влажности кожи, расположения электродов и многих других факторов, пульс, непроизвольные движения и моргания пациента, внешние электромагнитные поля, действующие на входной усилитель, дискретизация сигнала по уровню и другие явления создают помехи широкого частотного диапазона (см. Рис.). Нистагм на окулограмме узнается по его характерной пилообразной форме. Амплитуды, углы наклона и длительности зубцов имеют значительный разброс. Важнейшими диагностическими показателями нистагма являются его направление, средняя скорость медленной компоненты и параметры саккад.

Известны методы выделения нистагма с помощью многократной обработки окулограммы порядково-статистическими фильтрами [4]. Эти методы представляются достаточно сложными.

На рис. представлены результаты обработки окулограммы методом распознавания пилообразного сигнала. Так как медленная компонента нистагма по углу наклона соизмерима с низкочастотными помехами (вызванными медленными изменениями

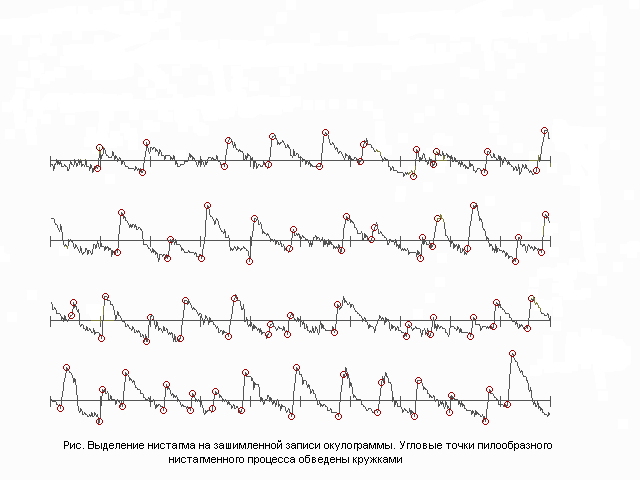
кожных потенциалов и дрейфом нуля усилителя), то распознаются только саккады, для чего используется алгоритм, описанный в разделе 4. Функция принадлежности (1) имеет пороговое значение =0.7. Прямые, связывающие конец некоторой саккады с началом следующей, принимаются за аппроксимации медленных компонент, которые обрабатываются стандартными статистическими методами: вычисляются средние значения длительности и скорости медленных компонент по всей записи окулограммы.

Литература

  1. Фомин Я.А., Тарловский Г.Р. Статистическая теория распознавания образов. М.: Радио и связь, 1986. 265 с.
  2. Вишняков А.Н. Выделение полезного сигнала на фоне помехи и псевдослучайного возмущения // АиТ.1997. № 10. С. 126-133.
    3.
  3. Heinonen P., Neuvo Y. FIR-median hybrid filters // IEEE Tr. On Acoustics, Speech and Signal Processing. 1987. Vol. ASSP-35. № 6. P. 832-838.
  4. Engelken E.J., Stevens K.W. A new approach to the analysis of nystagmus: an application for order-statistic filters // Aviat. Space Environ. Med. 1990. Vol. 61. P. 859-864.
Site of Information Technologies
Designed by  inftech@webservis.ru.