 |
||
ДОСТОВЕРНОСТЬ ОЦЕНИВАНИЯ ХАРАКТЕРИСТИК ПОГРЕШНОСТЕЙ РЕЗУЛЬТАТОВ МЕТРОЛОГИЧЕСКОГО АНАЛИЗА, ПОЛУЧАЕМЫХ С ПОМОЩЬЮ ТИПОВЫХ ИЗМЕРИТЕЛЬНЫХ ПРОЦЕДУР
И.А. Брусакова
Санкт-Петербургский Государственный электротехнический университет “ЛЭТИ
”им. В.И.Ульянова (Ленина)
Кафедра Информационно-измерительных технологий
Abstract –
For perposes of estimation of metrology reliability for virtual measuring nets. To organize of IMI is neсessary to formalize apriory knowleges of measuring procedures for main types of measuring nets. That is why the sutable analytic-algorithmic forms are presented in this paper. To provide these forms with reliability was applied metrological analysis of main metrological characteristics.Метрологический анализ может выполняться либо на экспериментальной, либо на теоретической основе. Метрологический анализ на теоретической основе разделяется, в свою очередь, на расчетное оценивание характеристик погрешностей результатов измерений и на их оценивание с помощью имитационного моделирования. Однако все большее частое использование так называемых виртуальных
[1 -2], [4 - 6], [7] и интеллектуальных средств измерений требует адекватного развития именно расчетных методов МА, обеспечивающих уменьшение временных затрат и эффективность параметрического синтеза.Объектом расчетного МА ВИЦ являются методические погрешности результата измерения. МА ВИЦ на теоретической основе предполагает оценивание характеристик методических погрешностей. Это вытекает из формальных определений полной, методической и инструментальной погрешностей.
То обстоятельство, что инструментальные погрешности обусловлены отличием реализуемых звеньями измерительной цепи преобразований от идеальных (принятых), влечет за собой необходимость проведения МА полных и инструментальных погрешностей на экспериментальной основе, так как порождаемые технологическими факторами и изменением условий отличия реальных характеристик ИС от номинальных иначе не учесть. В то же время, наличие сведений о номинальных характеристиках звеньев ВИЦ создает объективные условия для выполнения МА на теоретической основе, т.е. с использованием расчетов или имитационного моделирования
.Необходимым и достаточным условием для выполнения МА на теоретической основе является наличие соответствующих априорных знаний (АЗ) в виде математических моделей процедур, средств и условий измерений, включая входное воздействие, а также алгоритмического обеспечения оценивания требуемых характеристик погрешностей.
Возрастающая роль расчетных методов МА ВИЦ стимулирует,
во-первых, развитие соответствующего математического обеспечения, и,
во-вторых, выполнение работ по сближению номинальных и реальных характеристик ИС. Последнее достигается не только снижением уровня технологического разброса характеристик, но и уточнением номинальных характеристик как в виде учета их зависимости от условий (функций влияния), так и с помощью определения показателей разброса. Расчетное оценивание характеристик погрешностей результатов измерений основано на предположении, что погрешность – случайная величина.
В общем случае характеристики погрешностей определяются видом входного воздействия и свойствами составляющих измерительную цепь модулей. Соответствующие сведения представляются адекватными моделями. Оценки характеристик погрешностей определяются принятыми
характеристиками входного воздействия и измерительных модулей, представляемыми неадекватными моделями. Отличие неадекватных моделей от адекватных – один из факторов, обусловливающих недостоверность результатов метрологического анализа. Второй фактор – допускаемые при расчетном оценивании аппроксимации (фактор неидеальности).Развитие теории МА ВИЦ затрагивает вопросы обеспечения требуемой достоверности результатов оценивания характеристик погрешностей. Требуемая достоверность, таким образом, достигается посредством максимально полного учета всех факторов, обусловливающих недостоверность результатов метрологического анализа. Особенно плодотворными оказываются наши усилия по обеспечению требуемой достоверности результатов оценивания характеристик погрешностей в том случае, если получены удобные расчетные соотношения для определения достоверности для каждого модуля аналого-цифрового преобразования.
Ниже приводится детальное исследование достоверности расчетного оценивания характеристик погрешностей применительно к типовым видам адекватных и неадекватных моделей для некоторых процедур измерений и применительно к типовым аппроксимациям, используемым при расчетном оценивании.
В общем случае АЗАЦП Представляются совокупностью кортежей, объединенных конъюнкцией типа АЗАЦП = АЗД
& АЗК.Процедуру оценивания интервальной вероятности
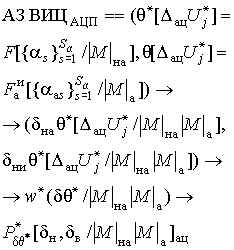 .
.
Рассмотрим механизм определения достоверности оценок МХ ВИЦ, построенных из модулей аналого-цифрового преобразования (ядро процедуры) и модулей нормализации ВИЦ Н-АЦП, преобразования рода величины с масштабированием и округлением результата измерения, фильтрации (аналоговой и цифровой): ВИЦ Р-АЦП-М-ОКР
, ВИЦАФ-АЦП, ВИЦАЦП-ЦФ.Обратим внимание на то, что часто не удается определять достоверность каждого конкретного модуля вне его взаимосвязи, например, с аналого-цифровым преобразованием (случай ВИЦ Р-АЦП-М-ОКР). Этот факт объясняется как крайней затруднительностью анализа погрешности неадекватности, которая в нашем случае максимально определяется неадекватностью входного сигнала, так и возможным наличием взаимно-корреляционных взаимосвязей между различными компонентами полной группы погрешностей ВИЦ. Поэтому особенно важно на этапе концептуализации и формализации предметной области метрологического анализа ВИЦ тщательно представлять как априорные знания, необходимые для метрологического анализа каждого модуля ВИЦ, так и АЗ, необходимые для МА конкретной ВИЦ, с
целью предварительного изучения взаимосвязей модулей ВИЦ, и, как следствие, возможностей получения удобных аналитико-алгоритмических форм для определения достоверности оценок МХ ВИЦ.Пусть необходимо произвести оценку достоверности преобразований, реализованных с помощью модуля нормализации. Очевидно, что в этом случае применяется схема оценки достоверности, предложенная в
[7] для модуля дискретизации.Выберем в качестве адекватной модели входного сигнала сигнал, представленый суммой трех компонент: нулевой, первой, второй производных некоторого напряжения
{Uj (t) = Uj , Uj(t) I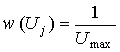 .
Тогда достоверность оценивания полной группы
погрешностей блока нормализации описывается как
.
Тогда достоверность оценивания полной группы
погрешностей блока нормализации описывается как
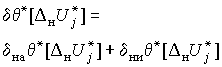 ,
,
далее приходим к следующим соотношениям:
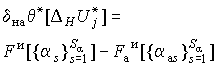
- ошибка из-за неадекватности используемых математических моделей ( идеальные функциональные преобразования
F и и Fа и связывают случайные и детерминированные параметры преобразования a для идеальной и адекватной моделей );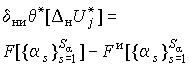
- ошибка из-за неидеальности вычислений ( возможные аппроксимации).
Далее необходимо использовать эти соотношения для определения ошибок оценивания, например, математического ожидания и среднего-квадратичного отклонения производится аналогично рассуждениям, приведенным в
[7].В случае анализа достоверности характеристик полной погрешности модулей нормализации и аналого-цифрового преобразования используются соотношения, для которых в случае оценок СКО необходимо учитывать взаимно-корреляционные функции между составляющими полной группы погрешностей. Так, в случае неадекватного входного воздействия получены соотношения для аналитического описания математического ожидания и СКО в предположении, что реализуемый коэффициент нормализации – случайная величина. Необходимо реализовать ту же процедуру для адекватного входного воздействия и перейти к получению расчетных соотношений для ошибок оценивания математического ожидания и СКО группы погрешностей нормализации и аналого-цифрового преобразования.
Предложим последовательность действий для определения достоверности при реализации ВИЦ в виде, например, последовательно соединенных модулей нормализации и модуля аналого-цифрового преобразования:
АЗн
® {U; w[U]; Rн(.) = a(.);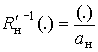 ; a, aн ; w[aн];
; a, aн ; w[aн];
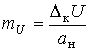 ;
;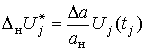 ;
;
w[![]() ]; M[
]; M[![]() ], D1/2 [
], D1/2 [![]() ]},
]},
где
U- вид входного воздействия, w[U ] –плотность распределения вероятности входного воздействия; Rн – вид оператора нормализации;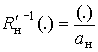 - вид оператора обратного
преобразования нормализации; a, aн – действительный и
реализуемый коэффициенты нормализации; w[aн]– плотность вероятности
коэффициента aн;
- вид оператора обратного
преобразования нормализации; a, aн – действительный и
реализуемый коэффициенты нормализации; w[aн]– плотность вероятности
коэффициента aн;
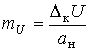 - коэффициент
масштабирования (в случае, если операция
нормализации предшествует операции
аналого-цифрового преобразования);
- коэффициент
масштабирования (в случае, если операция
нормализации предшествует операции
аналого-цифрового преобразования); 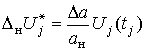 - погрешность нормализации; w[
- погрешность нормализации; w[Таким образом, процедуру оценивания достоверности МХ погрешности нормализации для определим следующей последовательностью отображений
АЗн®
® q [![]() ]® q *[
]® q *[![]() ]®
]®
® 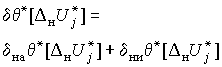 ®
®
® ![]() , (3.51)
, (3.51)
где
Априорные знания, необходимые для анализа достоверности МХ ВИЦ, представленной соединением блоков нормализации и аналого-цифрового преобразования, представим как
АЗ ВИЦ Н-АЦП = АЗ Н
& АЗАЦП. (3.52)Таким образом, процедуру оценивания достоверности МХ ВИЦН-АЦП определим в виде
АЗ
ВИЦН-АЦП ® [® w[![]() +
+![]() ]®
]®
® q [![]() +
+![]() ]®
]®
q * [![]() +
+![]() ]®
]®
® ![]() [
[![]() +
+![]() ]®
]®
® ![]() ,
,
где
Подход, предложенный выше, автор распространил на процедуры преобразования рода величины, фильтрацию. Алгоритмы оценивания достоверности метрологических характеристик типовых ВИЦ будут представлены в докладе.
Литература
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|