 |
||
|
||
энтропийная оценка системы поиска объекта в зоне неопределенности
С.В. Прокопчина, Е.А. Чернявский
Санкт-Петербургский государственный электротехнический университет “ЛЭТИ” им. В.И.Ульянова (Ленина)
Abstract
Для энтропийной оценки системы поиска объекта может быть использован функционал
[1]: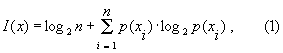
графическая интерпретация которого
для случая n=2 представлена на
рис.1, где n – количество
элементов зоны возможного расположения объекта.
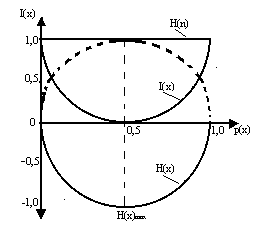
Рис.1. Графическая иллюстрация воспроизведения функционала
I(x) при n=2.В выражении (1) слагаемое
характеризует степень неопределенности состояния вероятностной системы, а функционал
характеризует степень снятия неопределенности системы, где
Из рис.1 следует, что при максимальном значении
H(x) значение функционала I(x) равно нулю, что указывает на то, что в этом случае имеет место “незнание”, то есть полная “неопределенность” местонахождения объекта.По мере уменьшения
H(x) до нуля (при p(x)=0 или p(x)=1) функционал I(x) принимает максимальное значение (в данном примере I(x)=1).Для оценки эффективности “системы поиска” может быть использован критерий:
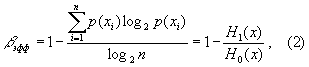
При этом
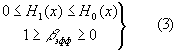
Здесь
– коэффициент эффективности поиска
объекта.
Значения вероятностей
задаются априорно
или определяются апостериорно на основании
практических данных.
Пусть некоторый акваторий с площадью
S разбит на 32 квадрата: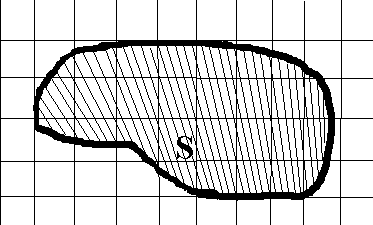
Рис.2. Разбиение акватория
Тогда, в случае равномерного выбора каждого из них (
n=32), энтропия будет иметь значение:
Примем априорно, что вероятность выбора только одного квадрата с находящимся в нем объектом будет:
а все остальные вероятности
.
Тогда, исходя из выражения:
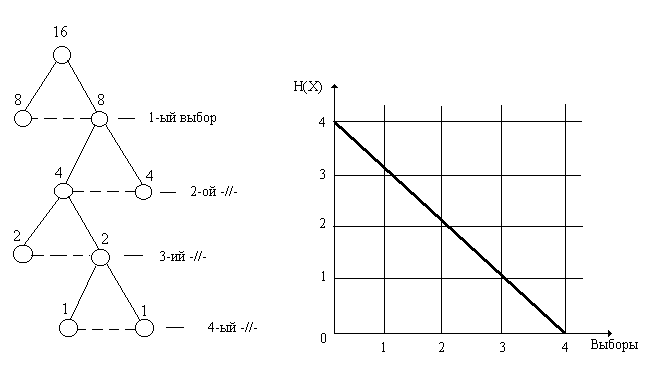
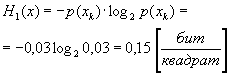
Эффективность поиска объекта для рассматриваемого упрощенного случая будет иметь значение:
В качестве другого возможного варианта решения задачи поиска объекта в зоне неопределенности может быть использован принцип определения минимального числа выборов.
Пусть объект
N расположен в одном из 16 квадратов акватория. Найдем минимальное число выборов при поиске объекта N. Дадим энтропийную оценку системы поиска, используя графическую иллюстрацию.При полном отсутствии априорной информации об объекте неопределенность местоположения будет:
Первый выбор произведем исходя из того, что одна (первая) половина квадратов полностью обследована и в ней объект не обнаружен.
В результате степень неопределенности системы поиска будет:
При втором выборе получим:
При третьем выборе:
При четвертом (последнем) выборе получим:
Таким образом, степень неопределенности системы поиска объекта для принятых условий изменяется от
до 
.
Графическая иллюстрация процесса поиска представлена на рис.3.
Рис.3. Иллюстрация процесса поиска объекта по принципу “выбора”.
Литература
1. Е.А. Чернявский. Анализ информационных процессов измерительно-вычислительных средств. Учебник. “Энергоатомиздат” (СПб Отд.), 1999.
2. Д.Д. Недосекин, С.В. Прокопчина, Е.А. Чернявский. Информационные технологии интеллектуализации измерительных процессов. Монография “Энергоатомиздат” (СПб Отд.), 1995.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|