 |
||
МЕТОД ОЦЕНКИ ДОСТОВЕРНОСТИ ОПЕРАТИВНОЙ ИНФОРМАЦИИ В РАСПРЕДЕЛЕННЫХ АСУ ТП
А
.А. Сидоров, Л.А. ШерешевскийНаучно–внедренческая фирма “Сенсоры, Модули, Системы”
Abstract – A lot of computations in modern distributed process control systems are performed upon data that is inevitably inaccurate. It is important to be able to estimate the influence of all errors (including those caused by untimely measurements and processing of data) on the system’s behavior. In order to obtain these estimates in real time it is suggested to use methods of self–validated computations. An extension of interval computations model is proposed and its use is justified.
Автоматизированные системы управления сложными технологическими процессами характеризуются большим числом контролируемых параметров (до нескольких тысяч) и распределенной архитектурой аппаратных средств сбора и обработки данных. Как следствие, корректная интерпретация результатов работы системы персоналом должна осуществляться с учетом многочисленных источников погрешностей и ошибок. К таким источникам относятся и изменения во времени точностных характеристик датчиков, и сбои в аппаратуре, и ошибки датирования результатов измерений [1], и ряд других факторов. Цена ошибочного решения, принятого на основе недостоверных данных, может быть недопустимо высокой. Все это вместе делает чрезвычайно актуальной разработку методики оценки качества получаемой оперативным персоналом информации в реальном времени.
Традиционные способы оценки достоверности оперативной информации в данной ситуации не приводят к успеху как минимум по двум причинам. Во–первых, в силу сложности современных объектов автоматизации, точные модели, описывающие их поведение, либо слишком громоздки для практического применения, либо отсутствуют вовсе. Во–вторых, неточности данных, обусловленные временным фактором, могут нетривиальным образом зависеть от текущего состояния распределенной системы [2].
Проблемы учета неточности измерительной информации и вычислительных ошибок достаточно эффективно решаются методами вычислений с автовалидацией (
self–validated computations) [3], среди которых наиболее широкое распространение получила интервальная математика [4, 5]. Однако, использование интервальной математики для оценки погрешностей, привносимых неточностью времени регистрации данных, не представляется возможным.В связи с этим предлагается внести некоторые дополнения в модель интервальной математики с тем, чтобы она позволяла автоматически, в качестве составной части самого вычислительного процесса оценивать возможную неточность значений параметров вследствие несинхронности измерений.
Пусть
Локус
Определим теперь арифметические операции над локусами. Вначале ограничимся рассмотрением локусов с совпадающими интервалами времени. Пусть
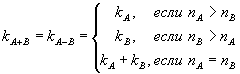 ,
,Операции над вырожденными операндами вводятся аналогичным образом, как естественное обобщение арифметических действий в интервальной математике.
Теперь рассмотрим операцию приведения двух локусов к общему временному интервалу. Пусть
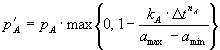 , где
, где Поясним теперь смысл введенных выше объектов и операций над ними. Наиболее важные компоненты локуса
Особый интерес представляет последний компонент локуса
Помимо этого, каждый локус содержит дополнительную информацию, используемую для подсчета достоверности результатов локусных арифметических операций. В частности, диапазон
Операция приведения временного диапазона определена исходя из предпосылки, что все измеряемые параметры объекта изменяются не быстрее, чем полиномиально. В любом случае, на конечном отрезке времени их можно ограничить некоторым полиномом, т.е. для каждого параметра
В заключение следует заметить, что локусные арифметические операции в качестве аргументов допускают как локусы, так и интервалы и вещественные числа.
Литература
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|