 |
||
|
ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ МУЛЬТИПЛЕКАТИВНОГО АЛГОРИТМА СИМПЛЕКС-МЕТОДА А. Б. Хакимова Puma_home@mail.ru Содержание Целью данной работы является доказательство перспективности дальнейшего развития предлагаемого алгоритма для решения задач линейного программирования путем его сравнения с мультипликативным алгоритмом симплекс-метода. Доказано, что алгоритм позволяет уменьшить по кубическому закону число арифметических операций, необходимых для решения задачи линейного программирования, уменьшить размерность и число ненулевых элементов мультипликаторов. Приводится теоретическое и экспериментальное сравнение эффективности алгоритмов. При построении предлагаемого алгоритма использован феноменологический подход, приведенный В.М.Лачиновым, А.О.Поляковым в работе [1]. С феноменологической и конструктивной точек зрения предлагаемый подход кратко опишем так. В проблемной области генерируются ограничения задачи, последовательно формируя вспомогательные задачи линейного программирования, содержащие соответственно 1,..,k,.. ограничений. Предлагаемый алгоритм последовательно выполняет построение описаний всего множества решений вспомогательных задач следующим образом. На итерации k алгоритма даны описание всего множества решений вспомогательной задачи, построенное на предыдущей итерации, и сгенерированное k-ое ограничение. Требуется перейти к описанию всего множества решений k-ой вспомогательной задачи. Сгенерированное ограничение меняет контекст описания всего множества решений вспомогательной задачи и инициирует переход к описанию k-ой вспомогательной задачи. Связь между ограничениями вспомогательной задачи отображается в системе ограничений. Система ограничений отображается в описании всего множества решений вспомогательной задачи. Таким образом, переход к описанию k-ой вспомогательной задачи это процесс изменения контекста и связей между ограничениями вспомогательной задачи. Остается привести построения описания всего множества решений вспомогательной задачи и перехода к следующему описанию. Предлагаемый подход к повышению эффективности мультипликативного алгоритма симплекс-метода раскрывается путем поэтапного решения следующих задач: 1. Построение модели алгоритма для ручного счета в строчной форме записи. Описание терминологии и семантики предлагаемого алгоритма, уменьшения размерности задач линейного программирования и построения решения, отличного от найденного решения. 2 . Описание методологии решения задач вручную путём решения задач на зацикливание симплекс-метода и уменьшение размерности, а также на построение решения, отличного от найденного решения. 3. Описание известного мультипликативного алгоритма симплекс-метода, который выбран в качестве аналога для последующего теоретического сравнения с предлагаемым алгоритмом. 4. Построение предлагаемого мультипликативного алгоритма в терминах мультипликативного алгоритма симплекс-метода. 5. Доказательство, что предлагаемый алгоритм позволяет уменьшить по кубическому закону число арифметических операций, необходимых для решения задачи линейного программирования. 6. Экспериментальное сравнение эффективности алгоритмов, которое подтверждает теоретическое сравнение. При изложении материала принят модельный подход, в основе которого лежит триада: принципиальная модель, диалектика развития принципиальной модели до реализуемой модели, реализуемая модель. Во-первых, такой подход позволит, не вдаваясь в детали, сосредоточить внимание на сравнении моделей. Во-вторых, сделать решающие выводы относительно принятых решений. В-третьих, самое главное, построить реализуемые модели. В данной работе различие принципиального и реализуемого алгоритмов будет опираться на следующий критерий: на каждой итерации принципиального алгоритма все вычисления могут осуществляться без ошибок округления. Следует отметить, что с точки зрения модельного подхода любой современный язык программирования имеет <вкус> и <запах> своих предшественников, так и предлагаемый алгоритм неизбежно несет черты алгоритма симплекс-метода. Пусть 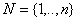 , ,
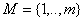 , ,
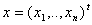 , ,
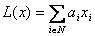 , ,
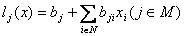 .
Рассмотрим задачу .
Рассмотрим задачу
(1) 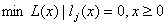 . .На каждой итерации предлагаемого алгоритма выполняется построение описания всего множества решений вспомогательной задачи, число которых равно числу ограничений. Каждая задача учитывает одно ограничение и во всех последующих задачах, ограничения, учтенные в предыдущих задачах, выполняются тождественно. Допустим, что (1) имеет решение. Тогда, вводя скалярную переменную 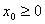 и достаточно большую скалярную величину
и достаточно большую скалярную величину
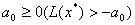 ,
где ,
где
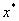 -
одно из решений (1), перейдем к эквивалентной задаче -
одно из решений (1), перейдем к эквивалентной задаче
(2) 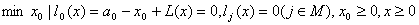 . .
Из (2) следует, что множество 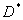 решений (1) совпадает с множеством неотрицательных решений уравнения
решений (1) совпадает с множеством неотрицательных решений уравнения
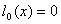 при минимальном значении критерия оптимальности
при минимальном значении критерия оптимальности
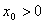 ,
удовлетворяющих ограничениям ,
удовлетворяющих ограничениям
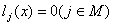 .
Если значение критерия оптимальности равно нулю, то в силу выбора скалярной
величины .
Если значение критерия оптимальности равно нулю, то в силу выбора скалярной
величины
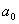 убеждаемся в неограниченности снизу критерия оптимальности
убеждаемся в неограниченности снизу критерия оптимальности
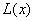 задачи (1).
задачи (1).
Пусть 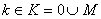 - номер итерации,
- номер итерации,
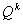 - множество, содержащее не более
- множество, содержащее не более
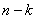 элементов множества
элементов множества
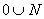 , ,
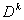 - множество неотрицательных решений уравнения
- множество неотрицательных решений уравнения
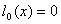 ,
обращающих в тождество ,
обращающих в тождество
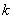 уравнений
уравнений
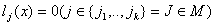 как при минимальном значении критерия оптимальности
как при минимальном значении критерия оптимальности
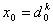 ,
так и при всех остальных ,
так и при всех остальных
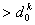 .
В приведенных обозначениях модель построения .
В приведенных обозначениях модель построения
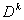 имеет следующий вид.
имеет следующий вид.
Если 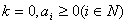 ,
то положить ,
то положить
(3) 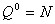 , ,
(4) 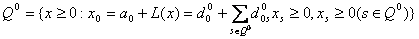 ; ;если 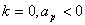 некоторого значения
некоторого значения
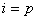 ,
то положить ,
то положить
(5) 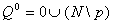 , ,
(6) 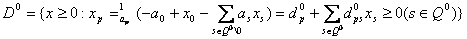 ; ;если 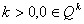 ,
то положить ,
то положить
(7) 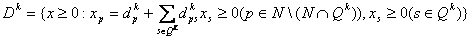 ; ;если 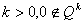 ,
то положить ,
то положить
(8) 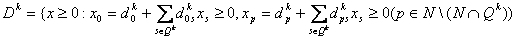 , ,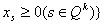 . .Пусть 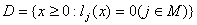 , ,
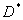 - множество решений задачи (1),
- множество решений задачи (1),
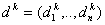 , ,
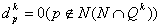 , ,
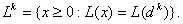 Тогда перечислим свойства описания
Тогда перечислим свойства описания
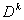 следующим образом:
следующим образом: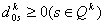 . .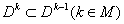 . .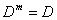 . .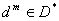 . .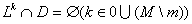 . .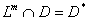 . .Пусть для некоторого значения 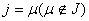 ,
тогда для перехода к описанию ,
тогда для перехода к описанию
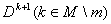 необходимо на множестве
необходимо на множестве
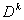 обратить уравнение
обратить уравнение
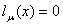 в тождество. Рассмотрим модель алгоритма перехода.
в тождество. Рассмотрим модель алгоритма перехода.Шаг 1. Построить уравнение связи (7) 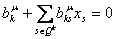 ; ;Подстановкой 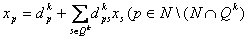 в уравнение
в уравнение
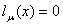 .
Не нарушая общности рассуждений, будем считать, что: .
Не нарушая общности рассуждений, будем считать, что:
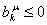 . .. Если 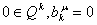 ,
то ,
то
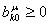 . .
Иначе (3) достаточно умножить на 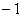 . .
Шаг 2. Провести анализ уравнения связи следующим образом: Если 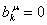 , ,
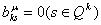 ,
то уравнение ,
то уравнение
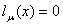 обращается в тождество на множестве
обращается в тождество на множестве
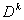 ,
то отсюда следует, что его можно удалить из числа ограничений. Не нарушая общности
рассуждений, такую ситуацию можно исключить из рассмотрения. ,
то отсюда следует, что его можно удалить из числа ограничений. Не нарушая общности
рассуждений, такую ситуацию можно исключить из рассмотрения.
Если 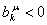 , ,
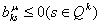 ,
то уравнение связи не разрешимо при любых значениях ,
то уравнение связи не разрешимо при любых значениях
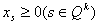 .
Отсюда следует несовместность ограничений задачи (1). Не нарушая общности
рассуждений, такую ситуацию можно исключить из рассмотрения. .
Отсюда следует несовместность ограничений задачи (1). Не нарушая общности
рассуждений, такую ситуацию можно исключить из рассмотрения.
Если 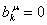 ,
а ,
а
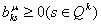 или
или
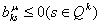 ,
то уравнение связи, а, следовательно, и уравнение ,
то уравнение связи, а, следовательно, и уравнение
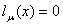 ,
обратятся в тождество тогда и только тогда, когда в описании ,
обратятся в тождество тогда и только тогда, когда в описании
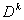 положить
положить
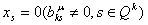 .
В результате перейдем к описанию .
В результате перейдем к описанию
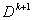 .
Это означает, что инструкцию можно сформулировать так: перейти к описанию .
Это означает, что инструкцию можно сформулировать так: перейти к описанию
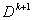 ,
полагая в описании ,
полагая в описании
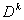
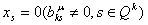 ,
и остановиться. ,
и остановиться.
Если 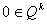 ,
то выбрать индекс ,
то выбрать индекс
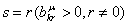 ;
иначе положить ;
иначе положить
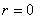 . .
Если 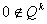 ,
то вычислить индекс ,
то вычислить индекс
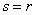 из соотношения
из соотношения
(10) 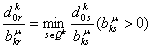 . .Шаг 3. Положить 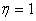 . .Шаг 4. Выразить 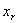 из уравнения связи (9) и подставить в описание
из уравнения связи (9) и подставить в описание
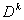 ,
переходя описанию множества ,
переходя описанию множества
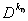 ,
положить ,
положить
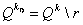 . .Шаг 5. Если 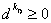 ,
то положить ,
то положить
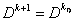 и остановиться; иначе перейти к шагу 6.
и остановиться; иначе перейти к шагу 6.Шаг 6. Вычислить индекс 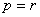 из соотношения
из соотношения
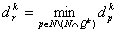 . .Шаг 7. Провести анализ уравнения связи (11) 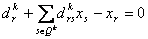 . .ограничения 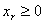 следующим образом:
следующим образом:
Если 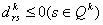 ,
то уравнение связи не разрешимо при любых значениях ,
то уравнение связи не разрешимо при любых значениях
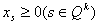 .
Отсюда следует несовместность ограничений задачи (1). Не нарушая общности
рассуждений, такую ситуацию можно исключить из рассмотрения. .
Отсюда следует несовместность ограничений задачи (1). Не нарушая общности
рассуждений, такую ситуацию можно исключить из рассмотрения.
Если 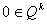 ,
то выбрать индекс ,
то выбрать индекс
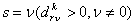 ;
иначе положить ;
иначе положить
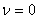 . .
Если 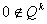 ,
то вычислить индекс ,
то вычислить индекс
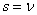 из соотношения
из соотношения
(12) 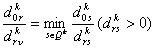 . .. Шаг 8. Выразить 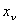 из уравнения связи (11) и подставить в описание
из уравнения связи (11) и подставить в описание
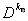 ,
переходя описанию множества ,
переходя описанию множества
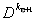 ,
положить ,
положить
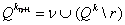 , ,
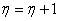 и перейти шагу 5.
и перейти шагу 5.
Примечание 1. Приведенная модель алгоритма допускает модификацию, которая заключается в отказе от проверки условия 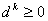 до тех пор, пока не будет учтено последнее ограничение.
до тех пор, пока не будет учтено последнее ограничение.
Примечание 2. Величину 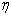 можно уменьшить, если индекс
можно уменьшить, если индекс
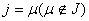 вычислять из соотношения
вычислять из соотношения
(13) 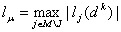 . .. Примечание 3. В случае ограничений неравенств 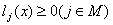 соотношение (13) требуется переопределить следующим образом
соотношение (13) требуется переопределить следующим образом
(14) 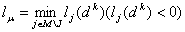 . .. Примечание 4. Пусть 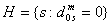 .
Если .
Если
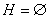 ,
то ,
то
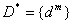 .
Иными словами, в этом случае решение задачи (1) единственно. Если .
Иными словами, в этом случае решение задачи (1) единственно. Если
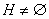 ,
то для построения ,
то для построения
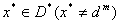 можно
решить задачу линейного программирования с произвольной целевой функцией от переменных можно
решить задачу линейного программирования с произвольной целевой функцией от переменных
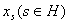 при ограничениях
при ограничениях
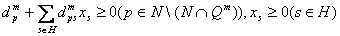 . .
Алгоритм предназначен для ручного счета, поэтому при описании примеров решения задач основной упор будет сделан на упрощении описания 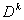 ,
таким образом, каким рекомендуется применять на практике. ,
таким образом, каким рекомендуется применять на практике.
Пример 1. На зацикливание алгоритма симплекс-метода [1, стр. 33]. 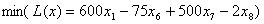 , ,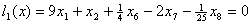 , ,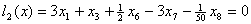 , ,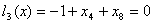 , ,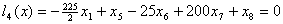 , ,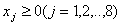 . .В соответствии с (5)-(6) начнем с описания 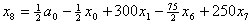 . .Из соотношения (13) 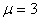 .
Построим уравнение связи .
Построим уравнение связи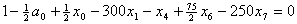 ограничения 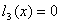 ,
откуда выразим ,
откуда выразим
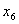 и подставим в описание. В результате получим
и подставим в описание. В результате получим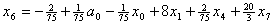 , ,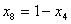 , ,Из соотношения (13) 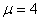 .
Построим уравнение связи .
Построим уравнение связи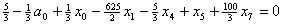 ограничения 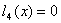 ,
откуда выразим ,
откуда выразим
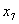 и подставим в описание. В результате получим
и подставим в описание. В результате получим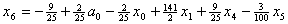 , ,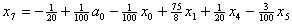 , ,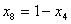 . .Из соотношения (13) 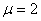 .
Построим уравнение связи .
Построим уравнение связи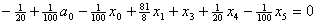 ограничения 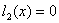 ,
откуда выразим ,
откуда выразим
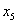 и подставим в описание. В результате получим
и подставим в описание. В результате получим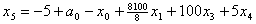 , ,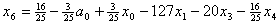 , ,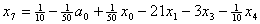 , ,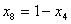 . .Из уравнения связи 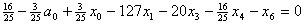 ограничения 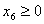 выразим
выразим
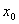 и
подставим в описание. В результате получим
и
подставим в описание. В результате получим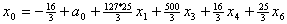 , ,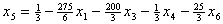 , ,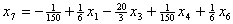 , ,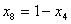 . .Из уравнения связи 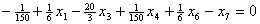 ограничения 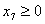 .
Из соотношения (12) .
Из соотношения (12)
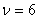 ,
поэтому выразим ,
поэтому выразим
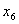 и подставим в описание. В результате получим
и подставим в описание. В результате получим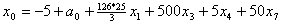 , ,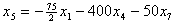 , ,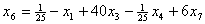 , ,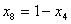 . .Из уравнения связи 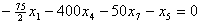 Следует, что 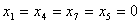 ,
поэтому перепишем описание следующим образом ,
поэтому перепишем описание следующим образом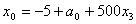 , ,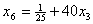 , ,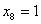 . .Из соотношения (13) 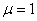 .
Построим уравнение связи .
Построим уравнение связи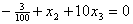 . .ограничения 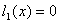 .
Из соотношения (10) .
Из соотношения (10)
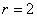 ,
поэтому выразим ,
поэтому выразим
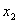 и подставим в описание. В результате получим
и подставим в описание. В результате получим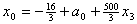 , ,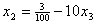 , ,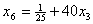 , ,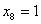 . .Отсюда следует, что 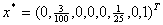 , ,
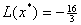 . .
Пример 2. С бесконечным количеством решений. 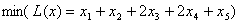 , ,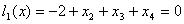 , ,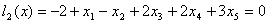 , ,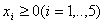 . .В соответствии с (3)-(4) начнем с описания 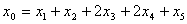 . .Из соотношения (13) 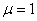 .
Построим уравнение связи .
Построим уравнение связи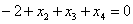 ограничения 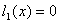 .
Из соотношения (10) .
Из соотношения (10)
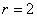 ,
поэтому выразим ,
поэтому выразим
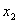 и подставим в описание. В результате получим
и подставим в описание. В результате получим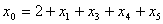 , ,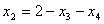 . .Из соотношения (13) 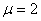 .
Построим уравнение связи .
Построим уравнение связи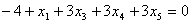 ограничения 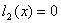 .
Из соотношения (10) .
Из соотношения (10)
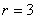 ,
поэтому выразим ,
поэтому выразим
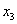 и подставим в описание. В результате получим 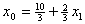 , ,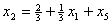 , ,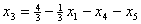 . .Отсюда 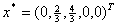 , ,
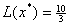 . .Для нахождения решения, отличного от найденного, решим задачу линейного программирования с произвольным критерием оптимальности, например 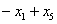 , ,при ограничениях 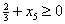 , ,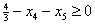 , ,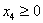 , ,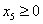 . .Подставляя решение этой задачи 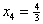 , ,
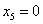 в описание, получим другое решение
в описание, получим другое решение
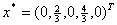 . .
Вычислительный опыт решения задач ЛП показал, что практичнее оказывается алгоритм, в котором для текущего базисного решения нет строгой обязательности выполнения условий задачи ЛП. Такой алгоритм более гибок и в тех случаях, когда найденный оптимальный базис используется в качестве начального для той же задачи с изменёнными условиями, не намного сложнее обычного и отличается только правилом выбора выводимой из базиса переменной. Обычно в литературе описание модели мультипликативного алгоритма (МА) симплекс-метода, связывают с выделением допустимой базисной системы ограничений следующим образом [2]. Рассмотрим задачу (15) 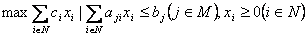 . .Пусть имеется базис  и базисная матрица
и базисная матрица
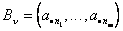 ,
а также мультипликативное представление матрицы ,
а также мультипликативное представление матрицы
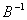 ,
где ,
где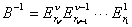 , , , ,
 , ,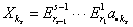 . .Здесь 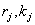 -
номера ведущих строк и столбцов на
-
номера ведущих строк и столбцов на
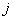 -ой итерации алгоритма. Очередная итерация алгоритма состоит из следующих шагов
{Чтобы не вдаваться в детали хранения мультипликаторов, обратную базисную матрицу будем
пересчитывать, а не представлять в виде произведения мультипликаторов, что упростит выкладки при сравнении эффективности
алгоритмов. Напомним, что при изложении материала принят модельный подход}
[3].
-ой итерации алгоритма. Очередная итерация алгоритма состоит из следующих шагов
{Чтобы не вдаваться в детали хранения мультипликаторов, обратную базисную матрицу будем
пересчитывать, а не представлять в виде произведения мультипликаторов, что упростит выкладки при сравнении эффективности
алгоритмов. Напомним, что при изложении материала принят модельный подход}
[3].
Шаг 1. Вычислить текущее двойственное решение вектора оценок строк по формуле: (16) 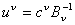 , ,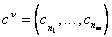 - вектор цен базисных переменных.
- вектор цен базисных переменных.
Шаг 2. Определить ведущий столбец, столбец для ввода в базис: 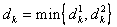 ,
где: ,
где:
(17) 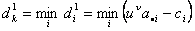 , ,
(18) 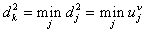 . .Если 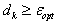 ,
то оптимум достигнут. ,
то оптимум достигнут.
Шаг 3. Разложить ведущий столбец по формуле: (19) 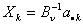 , ,если номер определялся из (3), и по формуле: (20) 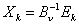 , ,если номер 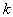 определялся из (4). Здесь
определялся из (4). Здесь
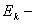
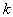 -ый
столбец единичной матрицы -ый
столбец единичной матрицы
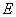 . .
Шаг 4. Вычислить номер ведущей строки из соотношения: (21) 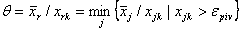 , ,где 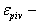 минимально допустимое значение ведущего элемента, выбираемое из соображений стабильности вычислительного процесса.
минимально допустимое значение ведущего элемента, выбираемое из соображений стабильности вычислительного процесса.
Шаг 5. Пересчитать базисное решение: (22) 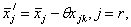
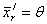 , ,пересчитать обратную базисную матрицу по формуле: (23) 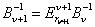 , ,где 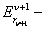 элементарная матрица, мультипликатор:
элементарная матрица, мультипликатор:
 . .Шаги с 1 по 5 повторяются до тех пор, пока не будет достигнут оптимум, или пока на шаге 4 не выяснится, что 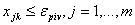 ,
т.е. решение задачи не ограничено. ,
т.е. решение задачи не ограничено.
Для упрощения теоретического сравнения эффективности алгоритмов выделим описание первого этапа - этапа построения описания 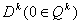 .
Для этого рассмотрим задачу .
Для этого рассмотрим задачу
(24) 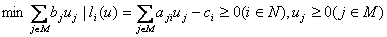 , ,двойственную задаче (14), и выберем параметр с > 0 , удовлетворяющий условию 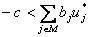 ,
где ,
где
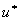 - решение задачи (24).
- решение задачи (24).Очередная итерация этапа 1 (построение описания 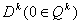 )
в терминах симплекс-метода состоит из следующих шагов. )
в терминах симплекс-метода состоит из следующих шагов.
Шаг 0. Определить номер ведущей строки из соотношения: 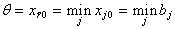 . .Если 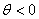 ,
то вычислить начальное двойственное решение вектора оценок строк по формуле: ,
то вычислить начальное двойственное решение вектора оценок строк по формуле:
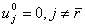 , ,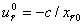 , ,вычислить обратную базисную матрицу по формуле: 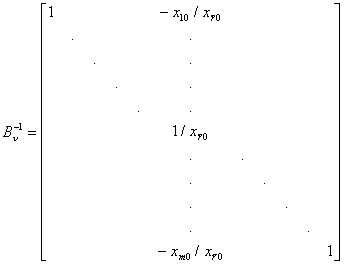 , ,положить 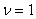 и перейти к шагу 1 этапа 1. Если
и перейти к шагу 1 этапа 1. Если
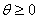 ,
то вычислить двойственное решение вектора оценок строк по формуле: ,
то вычислить двойственное решение вектора оценок строк по формуле:
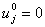 , ,вычислить обратную базисную матрицу по формуле: 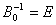 , ,где 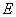 - единичная матрица, вычислить базисное решение по формуле:
- единичная матрица, вычислить базисное решение по формуле:
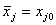 , ,положить 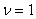 и перейти к шагу 1 этапа 2.
и перейти к шагу 1 этапа 2.
Шаг 1. Определить ведущий столбец, Столбец для ввода в базис: 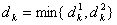 , ,где 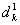 и
и
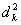 определяются из (17) и (18) соответственно. Если
определяются из (17) и (18) соответственно. Если
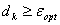 ,
то решение задачи неограниченно. ,
то решение задачи неограниченно.
Шаг 2. Разложить ведущий столбец по формуле (19), если номер 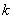 определяется из (17), и по формуле (20), если номер
определяется из (17), и по формуле (20), если номер
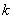 определяется из (18).
определяется из (18).
Шаг 3. Вычислить номер ведущей строки из соотношения: 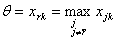 , ,Если 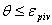 , ,
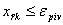 ,
то условия задачи ЛП несовместны; если ,
то условия задачи ЛП несовместны; если
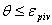 , ,
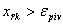 ,
то положить ,
то положить
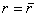 и перейти к шагу 4; если
и перейти к шагу 4; если
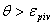 ,
то перейти к шагу 4. ,
то перейти к шагу 4.
Шаг 4. Пересчитать текущее двойственное решение вектора оценок строк по формуле: 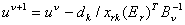 , ,где 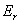 -
-
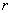 -ый
столбец единичной матрицы. -ый
столбец единичной матрицы.
Шаг 5. Пересчитать обратную базисную матрицу по формуле (23). Шаг 6. Если 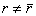 ,
то положить ,
то положить
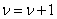 и
перейти к шагу 1 этапа 1. Если
и
перейти к шагу 1 этапа 1. Если
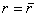 ,
то вычислить базисное решение по формуле: ,
то вычислить базисное решение по формуле:
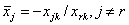 , ,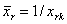 , ,положить 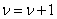 и перейти к шагу 1 этапа 2.
и перейти к шагу 1 этапа 2.
Очередная итерация этапа 2 (построение описания 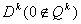 )
в терминах симплекс-метода состоит из следующих шагов. )
в терминах симплекс-метода состоит из следующих шагов.
Шаг 1. Определить ведущий столбец, столбец для ввода в базис: 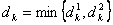 , ,где 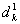 и
и
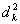 определяются из (17) и (18) соответственно.
определяются из (17) и (18) соответственно.
Если 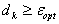 ,
то оптимум достигнут. ,
то оптимум достигнут.
Шаг 2. Разложить ведущий столбец по формуле (19), если номер 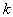 определялся из (17), иначе по формуле (20).
определялся из (17), иначе по формуле (20).
Шаг 3. Вычислить номер ведущей строки из соотношения (21). Если 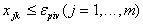 ,
то условия задачи несовместимы. ,
то условия задачи несовместимы.
Шаг 4. Пересчитать текущее двойственное решение вектора оценок строк по формуле (25). Шаг 5. Пересчитать базисное решение по формуле (22) и пересчитать обратную базисную матрицу по формуле (23). Шаги с 1 по 5 повторяются до тех пор, пока не будет достигнут оптимум, или пока на шаге 4 не выяснится, что 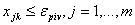 ,
т.е. условия задачи несовместны. ,
т.е. условия задачи несовместны.
Примечание. Начальное значение 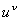 на шаге 1 можно получить, например, и по формуле (16) МА симплекс-метода.
на шаге 1 можно получить, например, и по формуле (16) МА симплекс-метода.
Сначала докажем, что модели алгоритмов генерируют одинаковую последовательность точек, а, следовательно, конечность и сходимость предлагаемого алгоритма. Затем проведём сравнение чисел арифметических операций, необходимых на очередной итерации моделей алгоритмов. Отсюда и последует вывод, что на очередной итерации, предлагаемого алгоритма, потребуется меньшее число арифметических операций. Доказательство конечности и сходимости непосредственно вытекает из доказательства следующей теоремы. Теорема. Пусть на очередной итерации 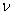 базис и базисная матрица на шаге 1 МА симплекс-метода совпадают с базисом и базисной матрицей на шаге 1 этапа 2
предлагаемого алгоритма, тогда модели алгоритмов генерируют одинаковую последовательность точек.
базис и базисная матрица на шаге 1 МА симплекс-метода совпадают с базисом и базисной матрицей на шаге 1 этапа 2
предлагаемого алгоритма, тогда модели алгоритмов генерируют одинаковую последовательность точек.
Доказательство. Теорема верна тогда и только тогда, когда: 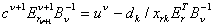 , ,Отсюда, полагая 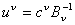 ,
получим: ,
получим:
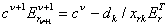 . .Так как 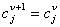 , ,
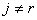 ,
то остается доказать, что: ,
то остается доказать, что:
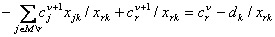 . .Возможны два случая (в первом номер 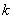 определялся из (3), а из (4) во втором).
определялся из (3), а из (4) во втором).
Случай 1. 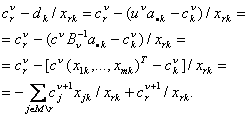
Случай 2.  отсюда и вытекает доказательство теоремы. При сравнении предположим, что матрица исходной задачи имеет плотность ненулевых элементов 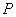 ,
но обратная матрица ,
но обратная матрица
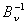 заполнена целиком. Очевидно, что различие в числе арифметических операций возникает на
шаге 1 МА симплекс-метода и шаге 4 предлагаемого алгоритма. Пусть задача (1) не вырождена (иначе не верна принципиальная
модель алгоритма МА симплекс-метода)
заполнена целиком. Очевидно, что различие в числе арифметических операций возникает на
шаге 1 МА симплекс-метода и шаге 4 предлагаемого алгоритма. Пусть задача (1) не вырождена (иначе не верна принципиальная
модель алгоритма МА симплекс-метода)
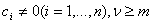 .
Тогда .
Тогда
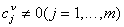 .
Отсюда следует, что выигрыш в числе арифметических операций умножений и сложений на очередной итерации равен .
Отсюда следует, что выигрыш в числе арифметических операций умножений и сложений на очередной итерации равен
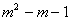 . .
Пусть для решения задачи (1) требуется 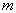 итераций, тогда общий выигрыш в числе арифметических операций равен
итераций, тогда общий выигрыш в числе арифметических операций равен
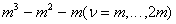 . .
В качестве критерия для сравнения эффективности алгоритмов принят показатель быстродействия, вычисляемый из соотношения: 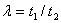 , ,где 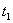 - время решения задачи модифицированным алгоритмом симплекс-метода, а
- время решения задачи модифицированным алгоритмом симплекс-метода, а
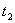 - время решения задачи предлагаемым методом.
- время решения задачи предлагаемым методом.
Таблица. Сравнение эффективности алгоритмов
Доказано, что предлагаемый алгоритм позволяет уменьшить по кубическому закону число арифметических операций, необходимых для решения задачи линейного программирования, уменьшить размерность и число ненулевых элементов мультипликаторов. В заключении следует отметить, что задача повышения эффективности алгоритмов линейного программирования является актуальной и занимает немаловажное место не только в решении экономических задач, но и в решении проблемы оптимизации и автоматизации технологических процессов. 1. Лачинов В.М., Поляков А.О. Инфординамика. Изд. СПбГТУ, СПб, 1999. 2. В. Н. Шевченко, Н. Ю. Золотых. Линейное и целочисленное программирование. // Учебное пособие. - Изд. Нижегородского Государственного Университета.- Нижний Новгород.- 2002. 3. Малков У.Х. Обзор путей повышения эффективности мультипликативного алгоритма симплекс-метода. //В сборнике Математические методы решения экономических задач. М.: Наука.- 1977 - №7.
|