 |
||
|
ПОВЫШЕНИЕ ЧИСЛЕННОЙ УСТОЙЧИВОСТИ МЕТОДА ИСКЛЮЧЕНИЯ ГАУССА М.В. Свириденко, А.Б. Хакимова MihaGod@mail.ru, Puma_home@mail.ru Аннотация Введение Обоснование поиска других подходов к построению прямых методов решения линейных систем Принципиальная модель алгоритма численной линейной алгебры Недостатки принципиальной модели алгоритма численной линейной алгебры Описание принципиальной модели предлагаемого алгоритма Пример Литература Предлагаемая модель алгоритма более устойчива к ошибкам округления. При этом все элементы системы уравнений остаются в области концепций и принципов проблемной области , где они и должны быть изначально, а переход элементов правых частей системы уравнений в область принципов формирования модели дает возможность управления механизмом переноса плохой обусловленности из одного места вычислений в другое. При построении модели алгоритма использован феноменологический подход, приведенный В.М.Лачиновым, А.О.Поляковым в работе "Инфординамика или Путь к Миру открытых систем [1]. С феноменологической и конструктивной точек зрения п редлагаемый подход кратко опишем так. В проблемной области генерируются уравнения задачи (система n линейных уравнений с n неизвестными), последовательно формируя вспомогательные задачи, содержащие соответственно 1,.., n уравнений. Предлагаемый алгоритм последовательно выполняет построение описаний всего множества решений вспомогательных задач следующим образом. На итерации k алгоритма даны описание всего множества решений вспомогательной задачи, построенное на предыдущей итерации, и сгенерированное k -ое уравнение. Требуется перейти к описанию всего множества решений k-ой вспомогательной задачи. Сгенерированное уравнени е меняет контекст описания всего множества решений вспомогательной задачи и инициирует переход к описанию k -ой вспомогательной задачи. Связь между уравнениям и вспомогательной задачи отображается в системе уравнен ий. Система уравнен ий отображается в описании всего множества решений вспомогательной задачи. Таким образом, переход к описанию k -ой вспомогательной задачи это процесс изменения контекста и связей между уравнен иями вспомогательной задачи. Остается привести построения описания всего множества решений вспомогательной задачи и перехода к следующему описанию. При изложении материала принят модельный подход, в основе которого лежит триада: принципиальная модель; диалектика развития принципиальной модели до реализуемой модели; реализуемая модель. В одних случаях принципиальная модель может совпадать с реализуемой моделью, а в других существенно отличаться. Все зависит от поставленных целей и решаемых задач. Подход принесет тройную пользу: во-первых, позволит, не вдаваясь в детали, сосредоточить внимание на концепциях {С точки зрения философии в основе любого алгоритма лежат идеи (концепции).} и принципах {Принципы формирования модели алгоритма будут описаны в порядке изложения материала} формирования моделей; во-вторых, сделать решающие выводы относительно принятых решений; в третьих, самое главное - построить реализуемые модели. Следует отметить, что с точки зрения модельного подхода любой современный язык программирования имеет «вкус» и «запах» своих предшественников, так и предлагаемый алгоритм неизбежно несет черты основного алгоритма численной линейной алгебры. Для обоснования разработки предлагаемого подхода к повышению численной устойчивости метода исключения Гаусса используем приём В. М. Вербжицского [2, стр. 84] следующим образом. Предположим, что методом Гаусса решается система 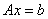 с матрицей коэффициентов с матрицей коэффициентов 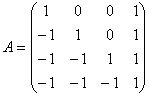 . . Приведение такой системы к треугольному виду прямым ходом метода Гаусса равносильно следующей последовательности эквивалентных преобразований матрицы 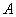 : : 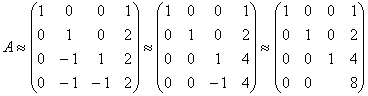 . . Очевидно, в случае 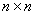 -матрицы такого типа прямой ход метода Гаусса допускает рост элементов
матрицы до величины -матрицы такого типа прямой ход метода Гаусса допускает рост элементов
матрицы до величины
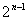 . При больших . При больших
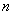 это может привести если не к переполнению разрядной сетки компьютера,
то к сильному влиянию погрешностей округлений, причём в данной ситуации не даст эффекта и постолбцовый выбор главного
элемента. это может привести если не к переполнению разрядной сетки компьютера,
то к сильному влиянию погрешностей округлений, причём в данной ситуации не даст эффекта и постолбцовый выбор главного
элемента. Рассмотренный пример оправдывает поиск других подходов к построению прямых методов решения линейных систем, возможно более сложных, чем метод Гаусса, но не допускающих большого роста элементов в процессе преобразований и, как следствие, численно более устойчивых. Пусть 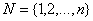 , ,
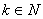 - номер итерации, - номер итерации,
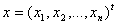 - вектор-столбец, - вектор-столбец,
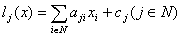 . Требуется найти в . Требуется найти в
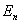 решение системы решение системы
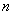 линейных уравнений с линейных уравнений с
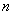 неизвестными неизвестными (1) 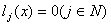 . . Сначала опишем принципиальную модель алгоритма численной линейной алгебры (алгоритм исключения Гаусса). При описании модели предположим, что система уравнений (1) имеет единственное решение и, что любая, выбранная нами, стратегия выбора ведущего элемента {Принцип формирования модели алгоритма} будет генерировать номера строк и столбцов в порядке возрастания их номеров (индексов). Это существенно упростит описание и позволит сосредоточить внимание на концепциях формирования модели алгоритма. Затем опишем недостатки и пути их преодоления. Следуя работе {Стратегия выбора ведущего элемента это первый принцип формирования модели алгоритма} , начнем с описания того, что на каждой итерации 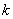 мы имеем дело с операциями двух видов. Одна из них – это деление на ведущий
элемент, чтобы найти число (пусть это будет мы имеем дело с операциями двух видов. Одна из них – это деление на ведущий
элемент, чтобы найти число (пусть это будет
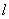 ), на которое надо умножить «ведущее» уравнение для последующего его
вычитания из уравнения, расположенного ниже. Затем, когда мы осуществляем это вычитание одного уравнения из другого, мы
непрерывно встречаемся с операциями «умножить-вычесть», т.е. члены одного ведущего уравнения умножаются на число ), на которое надо умножить «ведущее» уравнение для последующего его
вычитания из уравнения, расположенного ниже. Затем, когда мы осуществляем это вычитание одного уравнения из другого, мы
непрерывно встречаемся с операциями «умножить-вычесть», т.е. члены одного ведущего уравнения умножаются на число
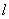 и вычитаются затем из уравнения, расположенного ниже. Для упрощения
договоримся называть каждое деление, и каждое умножение-вычитание простой операцией. В самом начале, когда первое уравнение
имеет и вычитаются затем из уравнения, расположенного ниже. Для упрощения
договоримся называть каждое деление, и каждое умножение-вычитание простой операцией. В самом начале, когда первое уравнение
имеет
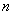 неизвестных, для получения в первом столбце каждого из нулей, требуется неизвестных, для получения в первом столбце каждого из нулей, требуется
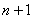 операций. Одна - чтобы найти множитель операций. Одна - чтобы найти множитель
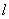 и и
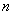 других - чтобы вычислить новые элементы соответствующей строки. Так как ниже
лежат других - чтобы вычислить новые элементы соответствующей строки. Так как ниже
лежат
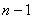 строк и, следовательно, требуется обратить в нуль строк и, следовательно, требуется обратить в нуль
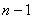 элементов первого столбца, находящихся ниже ведущего элемента, то первая
итерация процесса исключения требует элементов первого столбца, находящихся ниже ведущего элемента, то первая
итерация процесса исключения требует
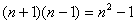 операций. После этого шага первый столбец не изменяется. Когда процесс
исключения подходит к операций. После этого шага первый столбец не изменяется. Когда процесс
исключения подходит к
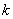 уравнениям, то для реализации следующей итерации требуется только уравнениям, то для реализации следующей итерации требуется только
 операций, чтобы обратить в нуль элементы столбца, находящегося под ведущими
элементами. Это эквивалентно первой итерации, когда операций, чтобы обратить в нуль элементы столбца, находящегося под ведущими
элементами. Это эквивалентно первой итерации, когда
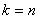 . Обратная подстановка идет значительно быстрей. Последнее неизвестное
находится с помощью одной операции (деление на ведущий элемент), предпоследнее требует две операции (умножение-вычитание и
затем деление) и т.д. На итерации . Обратная подстановка идет значительно быстрей. Последнее неизвестное
находится с помощью одной операции (деление на ведущий элемент), предпоследнее требует две операции (умножение-вычитание и
затем деление) и т.д. На итерации
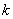 требуется только требуется только
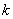 операций. Таким образом, общее число операций, необходимых для решения системы
(1), вычисляется по формуле операций. Таким образом, общее число операций, необходимых для решения системы
(1), вычисляется по формуле 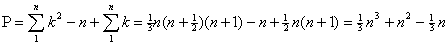 . . Отсюда следует, что в основе формирования модели лежат две концепции. Первая это отображение матрицы коэффициентов системы (1) в верхнюю треугольную матрицу, а вторая - обратная подстановка для нахождения каждого неизвестного. Описание недостатков начнем с концепции обратной подстановки. Концепция обратной подстановки для нахождения каждого неизвестного требует деления на соответствующий ведущий элемент. Независимо от стратегии выбора ведущего элемента нельзя гарантировать, что полученные значения переменных не будут сколь угодно большими. Иными словами любая стратегия выбора ведущего элемента не гарантирует численной устойчивости {Для доказательства численной устойчивости необходимо и достаточно доказать, что концепции и принципы формирования модели алгоритма гарантируют, что полученные значения переменных не будут сколь угодно большими} и возникает необходимость дальнейшего усовершенствования алгоритма, например, можно построить дополнительный блок для масштабирования строк {Стратегия масштабирования строк это второй принцип формирования модели алгоритма}, когда это необходимо {Необходимость масштабирования строк покажем на следующем примере. Для этого заменим матрицу коэффициентов системы уравнений (1) матрицей Гилберта для достаточно большого значения 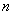 . Затем решим систему уравнений, округляя каждое число до нескольких значащих цифр. В результате на некоторой
итерации при вычислении новых элементов строк, находящихся ниже ведущего элемента, получим нули}. . Затем решим систему уравнений, округляя каждое число до нескольких значащих цифр. В результате на некоторой
итерации при вычислении новых элементов строк, находящихся ниже ведущего элемента, получим нули}. Теперь описание недостатков продолжим с концепции отображения матрицы коэффициентов системы (1) в верхнюю треугольную матрицу. Допустим, что блок для масштабирования строк построен и, что дополнительного принципа {Первый принцип - стратегия выбора ведущего элемента, второй - стратегия масштабирования строк} формирования модели алгоритма будет достаточно для доказательства численной устойчивости. Тогда, во-первых, нужно уметь распознавать ситуацию, когда масштабирование действительно необходимо. Во-вторых, потребуется определенное количество операций дополнительно. В-третьих, самое главное, масштабирование, когда это необходимо, применяется к новым (преобразованным) строкам, поскольку концепция отображения исходной матрицы коэффициентов в верхнюю треугольную матрицу для обращения в нуль элементов столбца требует на каждой итерации 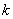 вычисления новых элементов строк, находящихся ниже ведущего элемента. вычисления новых элементов строк, находящихся ниже ведущего элемента. Напомним, что: не существует численного метода, который мог бы устранить чувствительность к малым возмущениям; если истинное решение чувствительно к малым возмущениям, то вычисленное значение не может обладать меньшей чувствительностью; единственное, что можно сделать – это перенести плохую обусловленность с одного места вычислений в другое. Первая концепция формирования модели алгоритма (отображение исходной матрицы коэффициентов в верхнюю треугольную матрицу) не гарантирует возможности управления механизмом переноса плохой обусловленности с одного места вычислений в другое. Описание предлагаемого алгоритма начнем с того, что модель алгоритма решения системы уравнений (1) разрабатывалась на стыке линейной алгебры и анализа, поэтому концепции и принципы ее формирования отличаются от концепций и принципов формирования описанной выше модели алгоритма исключения Гаусса. Введем обозначения: 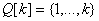 , ,
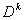 - описание множества решений системы - описание множества решений системы
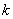 уравнений уравнений
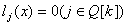 . Как и при описании принципиальной модели алгоритма исключения Гаусса,
предположим, что система уравнений (1) имеет единственное решение и, что любая, выбранная нами, стратегия выбора ведущего
элемента [8] будет генерировать номера строк и столбцов в порядке возрастания их номеров (индексов). . Как и при описании принципиальной модели алгоритма исключения Гаусса,
предположим, что система уравнений (1) имеет единственное решение и, что любая, выбранная нами, стратегия выбора ведущего
элемента [8] будет генерировать номера строк и столбцов в порядке возрастания их номеров (индексов). Это существенно упростит описание и позволит сосредоточить внимание на концепциях формирования модели алгоритма. Принципиальная модель алгоритма инициализации 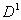 . .
Шаг 1. Вычислить номер 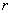 ведущей строки из соотношения ведущей строки из соотношения 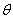
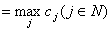
Согласно предположению 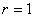 . . Шаг 2. Вычислить номер 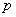 ведущего столбца из соотношения ведущего столбца из соотношения 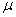
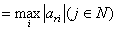 . .
Согласно предположению 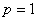 . . Шаг 3. Построить описание 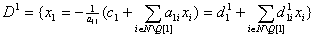 . . 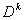 запишем так: запишем так: 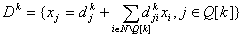 . . Концепция (идея), лежащая в основе формирования модели алгоритма, состоит в последовательном переходе от описания 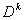 к описанию к описанию
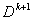 . Количество переходов равно . Количество переходов равно
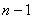 . . Принципиальная модель построения 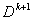 . . Шаг 1. Вычислить номер 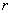 ведущей строки из соотношения ведущей строки из соотношения
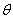
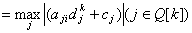 . . Согласно предположению 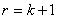 . . Шаг 2. Построить уравнение связи ведущей строки (2) 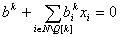 путем подстановки 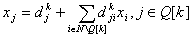 в уравнение 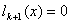 . . Шаг 3. Вычислить номер 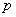 ведущего столбца из соотношения ведущего столбца из соотношения
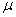
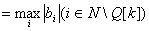 . . Согласно предположению 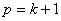 . . Шаг 4. Построить 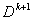 путем подстановки и добавления путем подстановки и добавления
(3) 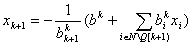 в описание 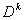 . . При вычислении числа арифметических операций, необходимых для решения системы (1), напомним, что мы договорились называть каждое деление и каждое умножение-вычитание простой операцией. Итак, для инициализации 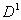 требуется требуется
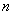 операций, построение уравнения связи (2) требует операций, построение уравнения связи (2) требует
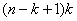 операций, а построение уравнения (3) и подстановка (3) в описание операций, а построение уравнения (3) и подстановка (3) в описание
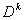 - -
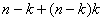 операций. Таким образом, общее число операций, необходимых для решения
системы (1), вычисляется по формуле операций. Таким образом, общее число операций, необходимых для решения
системы (1), вычисляется по формуле 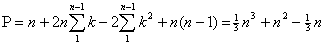 . . Практическое сравнение предлагаемого метода с методом исключения Гаусса Рассмотрим предлагаемый метод на примере с матрицей Гильберта с округлением до трёх значащих цифр после запятой: 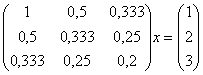 . . Вычислим номер 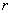 ведущей строки из соотношения ведущей строки из соотношения 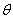
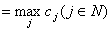 : : 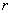
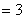 . . Вычислим номер 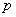 ведущего столбца из соотношения ведущего столбца из соотношения 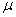
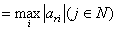 : : 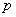
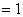 . . Построим описание 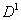
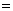
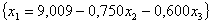 . . Вычислим номер следующей ведущей строки: 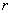
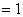 . . Подставим описание 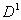 в первое уравнение: в первое уравнение: 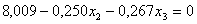 . . Вычислим номер следующего ведущего столбца: 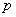
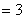 . . Построим описание 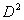
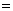
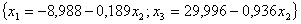 . . Построим уравнение связи ведущей строки подстановкой 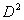 в последнее уравнение: в последнее уравнение: 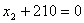 , , построим описание 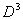
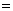
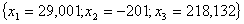 . . Вычислим для полученного решения 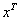
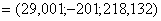 сумму модулей невязок сумму модулей невязок 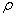
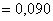 . . Решим задачу методом исключения Гаусса на примере с матрицей Гильберта с округлением до трёх значащих цифр после запятой. Для полученного решения 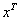
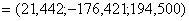 вычислим сумму модулей невязок вычислим сумму модулей невязок 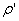
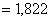 . . Очевидно, что 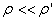 . . 1. Лачинов В.М., Поляков А.О. Инфординамика. Изд. СПбГТУ, СПб, 1999. 2. Вержбицкий В.М. Численные методы. Линейная алгебра и нелинейные уравнения. Издательский дом «ОНИКС 21 век», 2005. 3. Стренг Г. Линейная алгебра и ее применения. Издательство «Мир», Москва, 1980.
|