Глава 2. Объект 2-го порядка.
2.1. Математические модели объекта 2-го порядка.
2.2. Физические основы объектов 2-го порядка.
2.3. Практическое применение объектов 2-го порядка

Глава 2. Объект 2-го порядка.

2.1. Математические модели объекта 2-го порядка.

Объект 2-го порядка есть процесс преобразования объектов 1-го порядка.

Существуют 2 разновидности объекта 2-го порядка. Графически их можно

изобразить следующим образом:

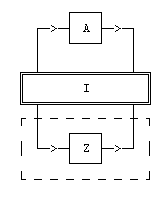
Объект класса 2.1

Объект класса 2.2

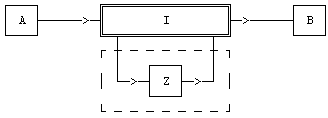
Остальные схемы являются сочетанием базовых.

Символы "A", "B" и "Z" обозначают объекты 1-го порядка. Символ "I"

обозначает интерпретатор объекта 2-го порядка - некий механизм,

обеспечивающий изменение объекта 1-го порядка, стоящего у него на выходе,

на основе информации получаемой от объекта 1-го порядка, стоящего у него

на входе. Математически объекты A и B можно описать как многомерные

переменные (точки в многомерном пространстве):

A(a1, a2, ... , an)

B(b1, b2, ... , bm)

Соответственно

|A|=|a1|*|a2|* ... *|an|

|B|=|b2|*|b2|* ... *|bm|

Математическую модель интерпретатора следует рассматривать как функцию

вида Y=I(X),

где X - входной объект 1-го порядка, Y - выходной объект 1-го порядка.

Причем X1, X2, ... , Xq - возможные состояния объекта X, q=|X|

Y1, Y2, ... , Yp - возможные состояния объекта Y, p=|Y|

Объект 1-го порядка "Z" является вспомогательным и служит для построения

функции Y=I(X). Он может как существовать, так и отсутствовать. В общем

случае ничего нельзя сказать ни о размерности пространства в котором он

существует, ни о |Z|. Он является подсистемой интерпретатора и может быть

невидим для стороннего наблюдателя. В принципе его можно рассматривать как

совокупность промежуточных переменных интерпретатора. Причины, по которым

происходят изменения объекта X, лежат за пределами теории объекта 2-го

порядка и мы рассматривать их не будем.

Рассмотрим теперь подробнее случаи 2.1 и 2.2.

Объект класса 2.1 описывается уравнением A=I(A). Решения этого уравнения

(если они существуют) представляют из себя набор определенных состояний

объекта A. Таким образом для внешнего наблюдателя этот случай можно в

принципе свести к объекту 1-го порядка C, состоящего из набора решений.

Приведем небольшой пример:

Дано:

A(a1,a2)

I(A)=(a1*a1-a1+1,a2*a2)

a1=(0,1,2,3,4,5)

a2=(0,1,2)

Найдем решения: нужно решить уравнение A=I(A). Для этого составим

такую систему уравнений:

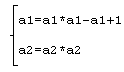
Решив эту систему найдем следующие корни:

a1=(1)

a2=(0,1)

Таким образом объект A может принимать 2 состояния:

A(1,0)

A(1,1)

Следовательно его можно без потери информативности для внешнего

наблюдателя заменить объектом 1-го порядка C, принимающем 2 возможных

состояния: C(1,0) и C(1,1).

Возможно также что в функции описания интерпретатора I(A) значения

переменных a1, a2, ... ,an будут зависеть друг от друга, т.е. возможно

существования уравнения типа a1=a1+a2; a2=a5-a10+a3*a1; a3=a4+a6; и т.д..

Рассмотрим случай объекта класса 2.2.

Уравнение интерпретатора примет вид:

B=I(A)

Соответствующая ему система уравнений:

В общем случае функции f1, f2, ..., fm могут быть произвольными (логическими

типа IF..THEN..ELSE, математическими и т.д.). Мощности объектов |A| и |B|

также могут быть любыми. Однако с практической точки зрения эти функции

должны быть хотя бы односторонне-однозначными, а |A|>=|B|, т.е. должно

выполнятся условие: при любом состоянии объекта A соответствующее ему

состояние B должно определяться однозначно. Обратное может быть и неверным.

Это требование наглядно представляется в виде графов:

1. |A|<|B|

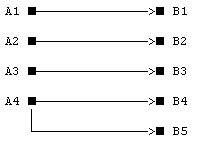
2. |A|=|B|

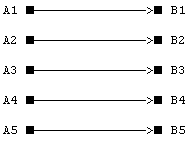
3. |A|>|B|

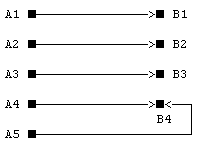
4. |A|=|B|, но в интерпретаторе имеются неоднозначные функции.

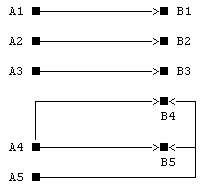
Здесь Ai (i=1...|A|) означает одно из состояний A, Bj (j=1...|B|) - одно

из состояний B. При |A|<|B| возникает неопределенность выбора состояния B

при определенном состоянии A (граф 1). Именно по этой причине применение

такой схемы невозможно на практике. Аналогичная неопределенность возникает

и в графе 4, где в интерпретаторе используются неоднозначные функции, в

результате чего в данном случае невозможно определить каким состоянием -

A4 или A5 были вызваны состояния B4 и B5. В дальнейшем такие объекты 2-го

порядка будем называть неопределенными, соответственно все остальные

объекты 2-го порядка - определенными (фактически на примере неопределенных

объектов показывается невозможность возникновения из ничего лишней

информации).

Классификация объектов 2-го порядка:

2.1.1 или просто 2.1 - замкнутый объект 2-го порядка.

2.2.1 - неопределенный разомкнутый объект 2-го порядка (или объект класса

2.2 в 1-й модификации).

2.2.2 - определенный разомкнутый объект 2-го порядка (или объект класса

2.2 во 2-й модификации).

2.2. Физические основы объектов 2-го порядка.

Объект 2-го порядка - это физический аналог математических формул.

Нечто, позволяющее в нашем реальном, физическом мире, преобразовывать

объекты 1-го порядка таким же образом, как математическая формула

позволяет изменять переменные. Только делается это не в абстракции, а в

реальности.

Для стороннего наблюдателя объект 2-го порядка представлен в виде 2-х

физических неоднородностей (A и B), состояния которых находятся в

определенной зависимости друг от друга. Причем определить со стороны что

является причиной, а что - следствием возможно лишь в случае когда

объект 2-го порядка определенный и |A|>|B|. В связи с этим возникает вопрос:

а нельзя ли представить объект 2-го порядка как объект 1-го порядка? Ведь

объект 2-го порядка тоже как бы является для внешнего наблюдателя

физической неоднородностью. А стало быть объекты 1-го и 2-го порядка не

имеют физических отличий, являясь по сути дела одним видом объектов. Здесь

кроется ошибка: только 2 части объекта 2-го порядка можно представить в

качестве неоднородности - А и В. Преобразователь физической

неоднородностью не является. Нельзя описать этот механизм при помощи

объекта 1-го порядка, а можно только привести примеры (формулу описания)

на то, как он себя проявляет, изменяя объект В. Во-вторых в объекте 2.2

порядка имеется зависимость состояния B от A. А в 2.1 состояния объекта A

могут принимать только определенные состояния, числом меньшим всех

возможных состояний, в то время как число возможных состояний обыкновенного

объекта 1-го порядка равно максимальному, причем по значение одних координат

многомерной переменной не зависит от других, в отличие от объекта класса 2.1.

Вот несколько примеров, относящихся к нашему миру.

К примеру, мы знаем что все тела, обладающие массой, притягиваются. Но мы

можем лишь только констатировать этот факт, только описать состояние этих

тел в результате гравитационного взаимодействия. Любые попытки описать

"устройство" гравитации приводят к появлению теорий, в которых гравитационное

взаимодействие разлагается на более "простые" составляющие, или наоборот,

представлено как частный случай чего-то более глобального. Однако и

составляющие, и общий случай опять-таки предстают только в примерах их

действия на материальные объекты. Примерах, как и раньше, ничего не

говорящих о их сути. Аналогично дела обстоят и с электрическим и с

магнитным полем и т.д.. "Причиной грома является молния, причиной молнии

является электрический разряд, причиной электрического разряда является

превышение напряженности электрического поля некоторой величины, причиной

превышения напряженности является . . .". В итоге при попытке объяснения

любого явления мы будем получать бесконечный ряд подобных причин. Таким

образом объект 2-го порядка - это вовсе не разновидность объектов 1-го

порядка, а совершенно другой вид объектов, являющийся более общим случаем

объекта 1-го порядка. Устройство интерпретатор невозможно описать через

объекты класса 1.1.

А это означает что для построения объектов 2-го порядка уже будет

недостаточно тех требований к среде функционирования, которые нужны для

построения объектов 1-го порядка (они оговаривались в главе, посвященной

описанию объектов 0-го и 1-го порядков). Необходимы более жесткие условия.

Что они должны из себя представлять? По всей видимости в результате их

введения должна появиться возможность создавать интерпретатор.

Интерпретатор у нас состоит из 2-х частей: физической - собственно

механизм преобразования, и логической - функции, описывающей процесс

преобразования. Отсюда следует что должно появиться 2 новых требования к

среде функционирования:

1) Между объектами А и В должно существовать взаимодействие

2) Это взаимодействие должно описываться неизменяющимися формулами

Само собой разумеется, что среда функционирования должна позволять строить

объекты 1-го порядка.

Рассмотрим случаи т.н. общих и синхронных осей. Если в объекте класса 2.2

объекты 1.1 имеют вид A(a1, a2, ..., c, an, an+1, ...) и

B(b1, b2, ..., c, bn, bn+1, ...), то c - общая ось. Если всегда значения

A и B на оси c равны, то ось c - синхронная ось. Так как значения объектов

A и B на синхронной оси всегда равны, то она является неинформативной - ее

всегда можно убрать из рассмотрения безо всякого ущерба.

В заключение осталось упомянуть понятие времени. Применительно к объекту

2-го порядка время служит синхронной координатной осью для объектов A и B.

Однако следует заметить что строго говоря, оно все-таки является не совсем

синхронной осью, так как его протекание зависит от массы материального

объекта и его скорости. Но при обычных нерелятивистских условиях этим можно

пренебречь.

2.3. Практическое применение объектов 2-го порядка

Сразу оговоримся: все рассматриваемые в этом пункте объекты 2-го порядка

определенные. Если при помощи объектов 1-го порядка хранятся данные, то

при помощи объектов 2-го порядка происходит их обработка. Алгоритм этой

обработки задается функцией интерпретатора Y=I(X). Однако сопоставлять

объекту 2-го порядка алгоритм неверно. Алгоритм есть описание какого-либо

процесса а не сам процесс. Однако есть возможность описать любой реальный

объект 2-го порядка при помощи алгоритма требуемой степени сложности, которая

определяется отдельно в каждом конкретном случае. Соответственно за объект

1-го порядка X принимается многомерная переменная входных данных алгоритма,

за Y - выходных данных. В силу условия определенности понятно, что при прочих

равных условиях, объект 2-го порядка будет наиболее простым при |X|=|Y|.

Естественно что для максимальной простоты для объектов A и B должны

отсутствовать синхронные оси.

Во всех остальных случаях он будет сложнее. Так как в состав объекта 2-го

порядка кроме X и Y входит еще интерпретатор, то в оценке суммарной

сложности следовало бы учитывать и его. Применительно к нашему миру

интерпретатор представляет из себя физические связи между объектами 1-го

порядка и вспомогательный объект 1-го порядка Z. Связи условно можно

представить как совокупность 2-х составляющих: их число и различия в

механизме работы разных связей. Оценить сложность механизма невозможно в

результате неизвестности его сути. Почему это так мы рассмотрели в пункте

2.2. С практической точки зрения все это означает что на каком-то этапе

построения алгоритма работы интерпретатора придется ввести в рассмотрение

своего рода примитивы - уже неделимые в данном рассмотрении материальные

объекты мира и обладающие конечным набором свойств, своего рода аксиомы.

Следовательно, сложность интерпретатора без учета Z можно приближенно

оценить широтой ассортимента используемых при его построении примитивов и

их числом. Сложность Z, как объекта 1-го порядка следует оценивать как

|Z|. Поэтому видимая сложность объекта 2-го порядка находится в зависимости

от |A|, |B|, рассматриваемых примитивов и |Z|. В заключении следует

отметить что в рамках объекта 2-го порядка отсутствует возможность

создания "из ничего" объектов 1-го порядка. Можно только преобразовывать уже

имеющиеся объекты 1-го порядка.

Очевидно, что подобно объектам 1-го порядка объекты 2-го порядка также

обладают свойством делиться на более мелкие объекты 2-го порядка и

быть частью более крупных объектов 2-го порядка. Причем объекты класса

2.1 и 2.2 могут быть представлены друг через друга: объект 1-го порядка A

в 2.1 может быть разделен на 2 объекта 1-го порядка C и D, причем значения

координат C и D, как многомерных переменных, будут находиться в зависимости,

задаваемой интерпретатором. Обратно: A и B в 2.2 рассматриваются как единый

объект C, координаты которого образуют подмножества a и b, связанные той же

зависимостью, что и исходном объекте 2.2.

Примеров объектов 2-го порядка можно привести множество - все созданные к

настоящему моменту человечеством машины и механизмы являются объектами

2-го порядка (как правило, это объекты класса 2.2).