return_links(); ?>

ВЯТКИН В.Б.

СИНЕРГЕТИЧЕСКАЯ ТЕОРИЯ ИНФОРМАЦИИ:
ОБЩАЯ ХАРАКТЕРИСТИКА И ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ

// Наука и оборонный комплекс – основные ресурсы российской модернизации: Материалы межрегиональной научно-практической конференции. Екатеринбург: УрО РАН, 2002.

Введение

1. Теоретические положения

1.1. Отражаемая (самоотражаемая) информация
1.2. Негэнтропия отражения
1.3. Отражение системных объектов через совокупность признаков
1.3.1. Отражение закрытых системных объектов.
1.3.2. Отражение открытых системных объектов.
1.3.3. Информационный закон отражения
1.4. Взаимосвязь иформационных функций IA , Ia , S с энтропией Больцмана 

2. Примеры практического использования

2.1. Анализ электронных систем атомов химических элементов
2.1.1. Система электронных подоболочек. 
2.1.2. Система s, p, d, f -подгрупп электронов.
2.1.3. Общие закономерности структурной организации.
2.2. Оценка структурной организации языковых текстов
2.3. Социально-политические аспекты
2.3.1. Критерии президентских и парламентских выборов.
2.3.2. К вопросу о численности парламентских партий и движений.
2.4. Прогнозно-геологические исследования

Заключение

Приложение ( Комментарий к термину "негэнтропия")

Литература и примечания

Введение

Современное научное познание характеризуется широким использованием идеологии системного подхода, в основе которого лежит отношение к исследуемым объектам как к системным образованиям (системам, подсистемам, системным объектам [1] ). При этом в процессе проведения исследований весьма часто анализируется взаимосвязь системных объектов, выделяемых в составе изучаемой системы, и, как следствие, возникает необходимость количественной оценки информации, отражаемой системными объектами относительно друг друга.
В общем случае процесс получения такой информации можно представить следующим образом. Сначала в составе некоторой системы D ( рис. 1 ) по признакам P_A и P_B , независимо друг от друга, выделяются два системных объекта A = {a | P_A (a)} и B = {b | P_B (b)}.

Пока познающему субъекту ничего неизвестно о наличии или объективном отсутствии в рассматриваемой системе третьего системного объекта K, такого, что K = A B =
= {k | P_A(k), P_B(k)}, он находится в состоянии неопределенности относительно отражения системных объектов A и B друг через друга. После выявления системного объекта K (или доказательства его отсутствия) эта неопределенность снимается и познающий субъект получает определенное количество отраженной информации I_{A« B} о каждом из объектов, которую разумно называть негэнтропией отражения. То есть негэнтропия отражения, являясь отраженной информацией, представляет собой снятую неопределенность отражения двух системных объектов друг через друга. Можно также сказать, что негэнтропия отражения является мерой воспроизведения друг через друга двух системных образований, каждое из которых рассматривается как единое целое.
Очевидно, что величина негэнтропии отражения I_{A« B} зависит от числа элементов m(A), m(B), m(K) в составе каждого из системных объектов A, B, K, соответственно. При этом отчетливо понимается, что при постоянстве значений m(A) и m(B), негэнтропия I_{A« B} является монотонно возрастающей функцией от m(K), принимающей свое максимальное значение, когда K=A и (или) K=B.
Поясним сказанное простым примером. – Пусть в некотором избирательном органе власти (система D) во фракцию A входит m(A) депутатов (системный объект A). Известно, что в процессе принятия решения по вопросу B, “за” проголосовало в общей сложности m(B) депутатов (системный объект B). Если теперь познающий субъект (аналитик) узнает, что среди множества депутатов, проголосовавших “за”, существует подмножество депутатов K в количестве m(K) человек, принадлежащих к фракции A ( системный объект K = A B ), то он получит определенное количество информации I_{A« B} (негэнтропии отражения), которую фракция A и множество депутатов, проголосовавших “за”, отражают друг о друге, как о целостных образованиях. При этом, очевидно, что чем больше величина m(K), тем большее значение имеет полученная информация I_{A« B}.
Актуальность количественного определения негэнтропии отражения и основанного на ней анализа системных образований, во многих областях знания не вызывает сомнений. Вместе с тем констатируется, что традиционная теория информации, изначально ориентированная на решение задач технической связи [ 2 ], не позволяет осуществить такое определение. Покажем это, пытаясь оценить негэнтропию I_{A« B} с помощью информационно-энтропийной меры К.Шеннона, занимающей в традиционной теории информации фундаментальное положение:

,                                                                      ( 1 )

где: p_i- вероятность появления какого-либо из N возможных событий, причем S p_i = 1;
K – коэффициент пропорциональности, зависящий от выбора единиц измерения. Основание логарифма при этом принято считать произвольным.

Из анализа формулы (1) следует, что информация по Шеннону является максимальной, когда все события имеют одинаковую вероятность (H = K log n) и равна нулю (H = 0), когда вероятность какого-либо события равна единице (появление такого события не дает никакой информации). Обращаясь теперь к рис. 1, нетрудно видеть, что в ситуации, когда системные объекты A и B отражаются друг через друга адекватным образом (рис.1д), использование формулы (1) покажет, что I_{A« B} = 0, так как вероятность встречи элементов aA и bB друг среди друга равна единице. Но это, в рассматриваемом контексте, является нонсенсом, поскольку негэнтропия отражения при A = B = K должна принимать свое максимальное значение. В связи с этим уместно привести высказывание самого К. Шеннона, понимавшего ограниченность сферы приложения своей теории: “Сознавая, что теория информации является сильным средством решения проблем теории связи, нельзя забывать, что она не является панацеей для инженера-связиста, а тем более для представителей всех других специальностей” [ 3 ].

Отмеченный недостаток существующей теории информации обусловлен тем, что ее математические основы традиционно разрабатывались под эгидой того, что информация атрибутивно связана с процессами управления и представляет собой снимаемую неопределенность выбора из множества возможностей. Другой же вид информации, объективно существующий в природе независимо от управления и генетически предшествующий ему [ 4 ], при этом остался в тени. К данному виду информации относится и негэнтропия отражения, которая, как было отмечено выше, также интерпретируется как снимаемая неопределенность, но, только уже не выбора, а отражения.

Изложенная проблемность количественного определения негэнтропии отражения инспирировала проведение информационно-теоретических исследований, ориентированных на решение познавательных задач, связанных с анализом отражения системных образований друг через друга. В настоящее время результатом этих исследований является вполне определившаяся теоретическая конструкция, получившая название – синергетическая теория информации. Такое название теории обусловлено рядом причин, в качестве основных из которых укажем следующие. – Предметом познания данной теории являются информационно-количественные аспекты взаимоотражения системных образований, включая такие его стороны как упорядоченность и хаотичность, а также особенности взаимоотношения последних при различных системно-структурных преобразованиях. При этом, как отражаемый, так и отражающий объекты рассматриваются в качестве единого целого, а их элементы, соответственно, обладают интегративными характеристиками и принимают участие в процессе отражения всей своей совокупностью. Поэтому, учитывая, что термин синергетика в переводе с греческого (synergetikos) буквально означает совместный, согласованно действующий [ 5 ] словосочетание синергетическая теория информации представляется вполне оправданным. В нижеследующем изложении, в тезисной форме, дается общее описание данной теории и приводятся примеры ее практического использования.

1. Теоретические положения

1.1.Отражаемая (самоотражаемая информация)

Определяя негэнтропию отражения I_{A« B} как информацию, которую системные объекты A и B отражают друг о друге, мы имеем в виду, что каждый из объектов представляет собой единое целостное образование. Поэтому, прежде чем вести речь о количественной стороне негэнтропии I_{A« B}, необходимо ответить на два вопроса: что следует в данном случае понимать под термином информация и что принимать за ее количественную характеристику. Отвечая на первый вопрос, будем исходить из общеупотребительного и наиболее простого определения информации, как сведений о чем-либо и, соответственно, конкретизируем это определение в наших исследованиях, как сведения о целом. Учитывая это, и, принимая во внимание тот факт, что при наличии равенства A = B = K взаимное отражение системных объектов A и B друг через друга не отличается от их отражения через самих себя, для ответа на второй вопрос рассмотрим самоотражение системного объекта A.

В качестве исходного начала примем очевидное утверждение, что системный объект А и каждый элемент соотносятся между собой как целое и его одноэлементная часть. Такое соотношение, рассматриваемое с диалектических позиций, обуславливает два существенных момента. Во-первых, целое не может состоять только из одного элемента и потому m(A) >= 2. Во-вторых, совокупность элементов, составляющих системный объект A, представляет собой не механическое собрание предметов, обладающих признаком P_A и существующих независимо друг от друга, а единое целостное образование, объединяясь в которое, элементы приобретают новые (интегративные) характеристики, не присущие им в их разобщенном виде. Естественно считать, что интегративные характеристики элементов представляют собой информацию, которая имеет количественное выражение, если характеристики обладают числовым показателем, функционально взаимосвязанным с общим числом элементов.

Интегративной характеристикой элементов является их индивидуальный символьный код, длина которого (число символов) функционально взаимосвязана с m(A). При этом разность длин кодов любых двух элементов не превышает один символ. Соответственно, за количество информации I_A, самоотражаемой системным объектом A, принята средняя длина L_ср(a) интегративного кода его элементов, как функция от m(A), то есть I_A = L_ср(a) = f (m(A)).

Исходя из интуитивного понимания того, что приращение

,

по мере роста m(A) уменьшается, сформулирована аксиома: для любых трех системных объектов A , B, C, таких, что m(A) = X – 1, m(B) = X , m(C) = X + 1, имеет место неравенство:

IB - IA > IC - IB.                                                                                    ( 2 )

С позиций аксиомы (2) установлено, что взаимно-однозначное соответствие между множествами значений I_A и m(A) наблюдается только тогда, когда интегративные коды элементов составлены с помощью двоичного алфавита. Согласно этому, формула I_A получена в следующем виде:

,                                                                                  ( 3 )

где x = [ log ₂ m(A) ] – целая часть log ₂ m(A).

При этом имеет место неравенство:

,

где - постоянная величина, выражающая точную верхнюю грань отклонения I_A от log ₂ m(A):

,

что наглядно иллюстрируют рис. 2 и рис. 3.

Так как при m(A) >> 1 значение становится пренебрежимо малой величиной в сравнении с I_A, то в практическом отношении может быть принято:

 [ 6 ].                                                                 ( 4 )

Таким образом, информация, отражаемая системным объектом A самим о себе, как едином целом, количественно характеризуется выражениями (3) и (4).

1.2. Негэнтропия отражения

Так как количество информации, самоотражаемой системными объектами, равно средней длине интегративного кода их элементов, то негэнтропия отражения в количественном отношении представляет собой результат воспроизведения средней длины интегративного кода элементов одного системного объекта через взаимодействующий с ним другой системный объект.

Системные объекты A, B, K в своей совокупности образуют простейшую систему информационной связи, в которой отражаемый (A) и отражающий (B) системные объекты являются, соответственно, источником и приемником информации , а связующий системный объект выступает в качестве передающей среды или канала связи. В результате анализа процесса передачи информации по такой системе связи установлено, что формула негэнтропии отражения I_{A« B}, в общем случае ( рис. 1б ), имеет вид:

,                                                                         ( 5 )

где I_K - информация, самоотражаемая системным объектом K.

С позиций выражения (5) и соответствующего ему анализа, негэнтропия отражения I_{A« B} определяется следующим образом: негэнтропия отражения друг через друга двух системных объектов есть информация, отражаемая каждым из объектов относительно другого объекта, численно равная общей части средней длины интегративного кода их элементов.

Отмечается, что существенные признаки системных объектов выступают в качестве их полноправных представителей и являются носителями негэнтропии отражения. Из этого следует, что формула (5) выражает также, как количество информации о системном объекте A, отражаемой признаком P_B, так и количество информации о системном объекте B, отражаемой признаком P_A. То есть, негэнтропия отражения, в общем случае, может быть определена так же, как информационно-количественная характеристика признаков системных объектов. В связи с этим, в нижеследующем изложении, понятия отражающий объект и отражающий признак используются как синонимы.

1.3. Отражение системных объектов через совокупность признаков

Рассмотрим информационные аспекты отражения системного объекта A через покрывающую совокупность непересекающихся между собой системных объектов B₁, B₂, … B_N, то есть, когда и o ( рис. 4 ).

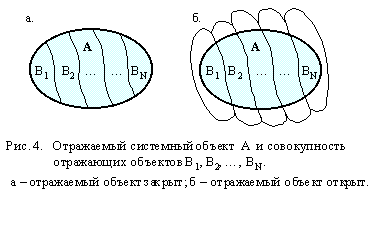
При этом предварительно отметим следующее.
а). Связующие объекты K₁, K₂, … K_N являются истинными системными объектами, то есть . Отсюда следует, что общее число отражающих объектов N связано с количеством элементов m(A) в составе отражаемого системного объекта A соотношением:

Соответственно, максимальное количество элементов в составе произвольного связующего объекта K_i, при заданном N, ограничено величиной разности m(A) – 2(N – 1). Короче говоря, значения m(K_i) удовлетворяют неравенству:

.

б). Отражаемый системный объект A, по отношению к окружающей среде (элементам дополняющего множества C = D \ A = ), может быть как закрытым, так и открытым в информационном отношении:
- Отражаемый системный объект является закрытым в информационном отношении ( рис. 4а ), если каждый из отражающих объектов является его подмножеством
- Отражаемый системный объект считается открытым в информационном отношении ( рис. 4б ), если хотя бы один из отражающих объектов не является его подмножеством .

1.3.1. Отражение закрытых системных объектов.

Отражаемый системный объект A посредством признаков P_B1, P_B2, … , P_BN делится на N качественно обособленных частей, совокупное отражение через которые отличается от его отражения через самого себя. Это отличие, прежде всего, заключается в том, что отражение через множество отражающих объектов характеризуется хаотичностью (рассеянностью, неопределенностью) или, иначе говоря, обладает энтропией. Естественно считать, что последнее, в информационном отношении, означает тот факт, что не вся информация I_A, отражаемая системным объектом A, как единым целым, отражается через совокупность его признаков и, та часть информации, которая остается неотраженной, является функцией энтропии отражения S и может служить ее числовой характеристикой. То есть энтропия отражения S представляет собой невоспроизведенную часть средней длины интегративного кода элементов , равную разности между отражаемой и отраженной информациями:

S = I_A - IS (6)

где: IS - аддитивная негэнтропия отражения системного объекта А через совокупностю признаков
P_B1, P_B2, … , P_BN.

После несложных преобразований выражение (6) приобретает следующий вид:

 .                                                                ( 7 )

Полученная формула энтропии отражения закрытого системного объекта математически тождественна энтропийной мере Шеннона (1), взятой при двоичном основании логарифма. Данный факт свидетельствует о том, что синергетическая теория информации и теория информации в версии Шеннона, имея предметом своего познания различные виды информации (связанной с управлением и существующей независимо от него), в то же самое время непосредственно взаимосвязаны между собой отношением взаимного проникновения друг в друга [ 7 ] и, как следствие, в своей совокупности образуют единую количественную теорию информации. Так как в наших рассуждениях энтропия отражения является вторичной, то есть выводимой через негэнтропию отражения функцией, то можно также утверждать, что в информационно-генетическом аспекте синергетическая теория информации является первичной по отношению к теории информации Шеннона.

В отношении собственно аддитивной негэнтропии IS и энтропии отражения S, приведя выражение (6) к виду:

IA = IS + S,                                                                               ( 8 )

особо отмечается следующее. – С диалектических позиций аддитивная негэнтропия и энтропия отражения являются взаимодополняющими противоположностями, в сумме всегда составляют постоянную величину (при фиксированном m(A)) и характеризуют отражение системных объектов с различных сторон: упорядоченности и хаотичности, соответственно. Так как совокупность качественно обособленных частей системного объекта выражает его структуру, а сам отражаемый системный объект при этом выступает в качестве системы, то аддитивную негэнтропию IS и энтропию S следует считать также соответствующими структурными характеристиками любых системных образований, представленных конечным множеством статистически равнозначных элементов.

На рис. 5 представлена диаграмма, образованная графиками максимальных и минимальных значений IS и S, как функций от N при фиксированном m(A).

Анализ диаграммы позволяет высказать следующее.
Графики IS ^min, IS ^max, S^min, S^max изначально образуют 2 контура: энтропийный abdefh и негэнтропийный или информационный cdfghb, которые локализуют соответствующие области всех возможных значений энтропии и аддитивной негэнтропии отражения закрытых системных объектов при заданном m(A) и произвольных значениях N и m(B_i). Взаимное пересечение этих контуров по точкам b и f позволяет выделить 3 интервала значений N (левый, центральный и правый) с присущими каждому интервалу особенностями взаимоотношений S и IS , определяющими в целом характер структурного отражения системных образований.

Отражение системных объектов, попадающих в левый интервал , характеризуется тем, что при любых соотношениях их частей между собой по количеству элементов, справедливо неравенство IS > S, то есть упорядоченность отражения превосходит его хаотичность.
В правом интервале наблюдается противоположная картина, когда при любых условиях имеет место неравенство S > IS , что соответствует погашению отражаемой информации и преобладанию хаоса над порядком.
В центральном интервале происходит пересечение областей возможных значений аддитивной негэнтропии IS и энтропии S, вследствие чего между ними здесь наблюдаются различные взаимоотношения. В общем случае IS и S могут быть как больше, так и меньше друг друга, но в ряде случаев, соответствующих прямолинейной области между точками b и f , имеет место их равенство между собой. В содержательном плане можно говорить, что в интервале значений N от до в отражении системных объектов наблюдается тенденция к взаимному уравновешиванию порядка и хаоса и может достигаться полное негэнтропийно-энтропийное (информационно-энтропийное) равновесие, когда отражение системного объекта, как единого целого, является насколько хаотичным настолько и упорядоченным.

Отмеченные особенности отражения позволяют все системные образования классифицировать, в зависимости от числа их качественно обособленных частей и вида соотношения аддитивной негэнтропии IS и энтропии S, на 5 типов:

- упорядоченные: ;
- хаотично-упорядоченные: ;
- равновесные: ;
- упорядоченно-хаотичные: ;
- хаотичные: .
Кроме приведенной классификации любые системные образования можно сопоставлять между собой по информационно-энтропийному отношению, именуемому R-функцией:

.                                                                                               ( 9 )

Количество качественно обособленных частей и их соотношение между собой по числу элементов определяют в целом структурную организацию системных объектов, а аддитивная негэнтропия IS и энтропия S являются мерами ее упорядоченности и хаотичности, соответственно. То есть R-функция представляет собой обобщенную информационно-энтропийную характеристику структурированности системных образований, значение которой говорит о том, что и в какой мере преобладает в их структурной организации: порядок (негэнтропия) или хаос (энтропия). Так, если R > 1, то в структурной организации преобладает порядок, в противном случае, когда R < 1 - хаос. При R = 1 хаос и порядок уравновешивают друг друга, и структурная организация системных образований является равновесной.

1.3.2. Отражение открытых системных объектов.

При открытии отражаемого системного объекта происходит его взаимодействие и обмен информацией с окружающей средой. Собственно отражение при этом становится более неопределенным, рассеянным, хаотичным, вследствие чего его энтропия увеличивается, а негэнтропия, как совокупная отраженная информация, соответственно уменьшается. Анализируя рис. 5, нетрудно придти к выводу, что новые возможные значения максимальной энтропии и минимальной негэнтропии при открытии системного объекта должны располагаться, соответственно, выше и ниже линий S^max и I^min, и при асимптотически выходить на линии ck и al. Данный факт говорит о том, что независимо от степени открытости отражаемого объекта область, ограниченная прямоугольным контуром ackl, включает в себя все возможные значения отраженной (негэнтропия) и неотраженной (энтропия) информации, вследствие чего эта область именуется информационным полем отражения.

Так как энтропия S характеризует отражение только закрытого системного объекта (это непосредственно следует из выражения (7)), то общее увеличение энтропии отражения, при его открытии, происходит за счет появления дополнительной энтропийной составляющей , имеющей определенную самостоятельность. Исходя из соблюдения баланса между отражаемой информацией, с одной стороны, и отраженной и неотраженной информациями, с другой стороны, величина определяется через уменьшение аддитивной негэнтропии отражения, соответствующей закрытому состоянию отражаемого системного объекта:

,                                                                          ( 10 )

где - аддитивная негэнтропия отражения системного объекта в его открытом состоянии.
После несложных преобразований выражение (10) приводится к виду:

                     ,
где  - коэффициент открытости i-го признака.

Учитывая, что энтропия S является функцией внутреннего строения отражаемого объекта, а дополнительная энтропия представляет собой опосредованную через признаки функцию его взаимоотношений с окружающей средой, то, при общем рассмотрении отражения системных образований, они получают соответствующие названия – внутренняя (S) и внешняя энтропия отражения.

1.3.3. Информационный закон отражения.

Информационно-энтропийный баланс отражения системных объектов, в общем случае, имеет вид:

                                                                     ( 11 )

Выражение (11) является устойчивым, однозначным соотношением между отражаемой, отраженной и неотраженной информациями, справедливым для любых системных объектов, представленных конечным множеством элементов (при выражение (10) сводится к выражению (8)). В соответствии с этим ему придается статус закона с названием информационный закон отражения, который формулируется следующим образом: при отражении системных объектов, через покрывающую совокупность непересекающихся между собой признаков (других системных объектов), происходит разделение отражаемой информации на отраженную и неотраженную части, первая из которых равна аддитивной негэнтропии, а вторая – сумме внутренней и внешней энтропий отражения.

Установленный закон, как по своей математической форме, так и по содержанию, подобен законам сохранения (энергии, количества движения и т.д.), присущим абстрактным физическим системам [ 8 ]. Системным показателем здесь, сохраняющим свое постоянное значение при любых структурно-системных преобразованиях (происходящих без изменения общего числа элементов в составе отражаемого объекта), является суммарная величина хаоса (энтропии) и порядка (негэнтропии), наблюдаемых в отражении системного образования. При этом необходимо отметить, что, когда отражаемый объект является открытым в информационном отношении, то постоянство суммы хаоса и порядка относится к системе отражающих объектов (признаков), а когда отражаемый объект закрыт, то это постоянство является также и достоянием структуры отражаемого системного образования.

1.4. Взаимосвязь информационных функций I_A , Ia , S с энтропией Больцмана.

При анализе отражения термодинамической системы A, состоящей из N идеальных газов
B₁, B₂, …, B_N, установлено следующее. – Энтропия Больцмана системы в ее структурно-упорядоченном состоянии (E₀) и в состоянии термодинамического равновесия (E_R), а также энтропия смешения газов , в соответствии с огрубленной формулой Стирлинга [ 9 ], приближенно равны:

, , ,                      ( 12 )

где: , k - постоянная Больцмана.

Из выражения (12) следует, что уравнение перехода системы идеальных газов из структурно-упорядоченного состояния в состояние термодинамического равновесия, и выражение информационного закона отражения (11) для случая закрытых системных образований, при неограниченном возрастании m(A), асимптотически эквивалентны друг другу, то есть:

~ .                                ( 13 )

Формулы (12) и вытекающая из них асимптотическая эквивалентность (13) свидетельствуют о непосредственной взаимосвязи синергетической теории информации со статистической термодинамикой. Этот факт позволяет утверждать, что разрабатываемая теория, имея предметом своего познания информационно-количественные аспекты отражения системных образований, по своей сущности является физической теорией. Не исключено, что нечто подобное имел в виду академик С.И. Вавилов, делая в 1935 году следующее предположение: “Может случиться так, что будущая физика включит как первичное, простейшее явление “способность сходную с ощущением”, и на ее основе будет объяснять многое другое” [ 10 ].

2. Примеры практического использования

Традиционная теория информации, оформившись как научное направление в 50-х годах 20-го века, практически сразу привлекла к себе внимание ученых и специалистов из различных областей знания. Достаточно сказать, что уже в 1956 году К.Шеннон писал: “Теория информации нашла применение в биологии, психологии, лингвистике, теоретической физике, экономике, теории организации производства и во многих других областях науки и техники” [ 11]. Вместе с тем, изложенный материал свидетельствует, что теория информации в версии Шеннона оперирует только с одной (S) из четырех информационных функций (), характеризующих отражение системных образований через совокупность отражающих объектов и, соответственно, использует только часть информационного поля отражения (рис. 5 – область, ограниченная графиками S^min и S^max ). Учитывая это, следует ожидать, что синергетическая теория информации найдет более широкую сферу приложения и сможет решать новые познавательные задачи, как теоретического, так и прикладного характера, недоступные для традиционной теории информации. Ниже приводятся примеры решения таких задач в различных областях знания.

2.1. Анализ электронных систем атомов химических элементов.

2.1.1. Система электронных подоболочек.

При анализе взаимосвязи структур электронных систем атомов химических элементов с их свойствами внимание исследователей, как правило, концентрируется на распределении электронов по наружным оболочкам, "отвечающим" за химические свойства элементов. Структура внутренних оболочек и электронных систем в целом при этом остается в тени. С целью выяснения вопроса о наличии взаимосвязи свойств атомов химических элементов со структурой их электронных систем, как целостных образований, проведено определение значений R-функции последних по совокупности электронных подоболочек.

Анализ полученных результатов позволяет высказать следующее. График зависимости значений R-функции от порядкового номера элементов Z ( рис. 6 ) имеет периодический, в целом затухающий характер. В горизонтальном направлении периодической системы Менделеева во всех рядах наблюдается одна и та же закономерность: последовательное понижение значений R-функции в начале ряда и повышение значений по мере приближения к его концу.

Большой интерес представляет график приращений ( рис. 7 ), периодический характер которого особенно отчетливо согласуется с периодическим изменением свойств химических элементов: в пределах каждого ряда, на всем его протяжении, значение последовательно увеличивается, а при переходе в начало следующего ряда резко падает. Из данного факта следует, что,возможно, является обобщенной количественной характеристикой ослабления металлических свойств и усиления металлоидных при последовательном переходе от одного химического элемента к другому.

В пределах вертикальных групп таблицы Менделеева ( рис. 8 ) также наблюдается устойчивая взаимосвязь изменения значений R-функции и свойств химических элементов: более сильному выражению металлических свойств элементов четных рядов больших периодов относительно элементов нечетных рядов и усилению металлических свойств в главных подгруппах элементов с увеличением номера больших периодов, соответствует понижение значений R-функции.

На основании сказанного периодический закон Д.И. Менделеева получает следующую интерпретацию: периодичность изменения свойств химических элементов является отражением периодического изменения значений R-функции электронных систем атомов, определенной по совокупности электронных подоболочек.

2.1.2. Система s, p, d, f -подгрупп электронов.

На рис. 9 представлен график R-функции, определенной по совокупности s, p, d, f -подгрупп электронов.

Данный график имеет ярко выраженный периодический характер и включает в себя 4 периода с числом элементов: 1-й период – 2, 2-й – 16, 3-й – 36, 4-й – 64. При этом нетрудно видеть, что каждый период, за исключением 1-го, точно охватывает 2 периода таблицы Менделеева. Из анализа распределения элементов по указанным периодам следует, что общая формула числа элементов в периоде (m(n)) имеет вид:

                                                                         ( 14 )

где: n - номер периода, k_n- степенной коэффициент, принимающий значения: (принципиально k₁ может иметь любое значение), k₂ = 1, k₃ = 0, . На протяжении 2-4 периодов график имеет форму бегущей волны (общий резкий спад значений в начале периода и относительно плавное их повышение при движении к его концу), в соответствии с чем эти три периода именуются волновыми. В пределах волновых периодов отношение числа элементов в нисходящей части графика к числу элементов в восходящей части остается постоянным и равно n² : 3n². Соответственно, число элементов в волновом периоде определяется по формуле:

m(n) = 4 n2                                                                                       ( 15 )

После подстановки (14) в (15) получается уравнение:

,

которое, как нетрудно видеть, при n > 4 не имеет решения. Иначе говоря, волновых периодов может быть только три. На этом основании делается вывод, что в природе потенциально существует только 2 + 16 + 36 + 64 = 118 химических элементов. При этом 118-й элемент завершает 7-й период таблицы Менделеева и, соответственно, является инертным газом (на рис. 9 этот химический элемент условно обозначен как If – информаций).

2.1.3. Общие закономерности структурной организации.

а). Структурную эволюцию электронных систем атомов химических элементов можно представить в виде следующей цепочки явлений:

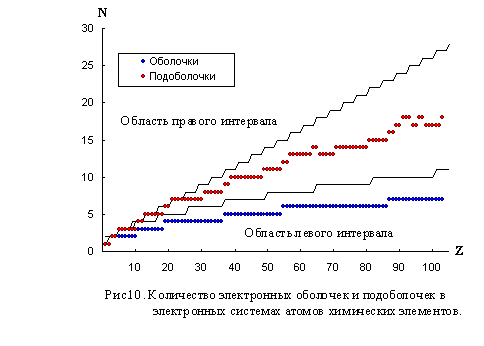
Анализ изменения значений R-функции, как внутри отдельных звеньев приведенной цепочки, так и при переходе от одного звена к другому, показывает следующее. – У нерасчлененной (однородной) совокупности электронов энтропия отражения отсутствует, поэтому для первого звена эволюционной цепочки принимается . Значения R-функции электронных систем, дифференцированных по оболочкам, варьируют в интервале от 1,0 до 3,6 при среднем значении 1,93. То же самое, для электронных систем, разделенных на подоболочки, составляет: варьирование – от 0,63 до 1,71; среднее значение – 0,82. При этом процесс дробления оболочек на подоболочки сопровождается уменьшением модуля разности R – 1 и согласованным переходом электронных систем из левого интервала значений N в центральный интервал ( рис. 10 ). (Здесь, как и прежде, N - количество обособленных частей системного образования.)

б). Объединенная совокупность электронов всех атомов химических элементов таблицы Менделеева представляет собой систему, в пределах которой общее число элементов каждого атома образует системный объект. Такая система относится к семейству систем натурального ряда, характеризующихся тем, что соотношение частей (системных объектов) по количеству элементов выражается натуральным рядом чисел или, иначе говоря, числу элементов в части соответствует ее порядковый номер. (Например, выражение: “N-я система натурального ряда”, говорит о том, что в структуре системы выделяется N частей, в первой из которых содержится 1 элемент, во второй – 2 элемента, … , в N-й – N элементов.) График на рис. 11 показывает, что R-функция систем натурального ряда, при последовательном увеличении N, монотонно возрастает и асимптотически приближается к единице. Соответственно, можно сказать, что точно также ведет себя и R-функция объединенной электронной системы атомов в процессе увеличения общего разнообразия химических элементов.

в). Превращения химических элементов, обусловленные радиоактивным распадом ядер, сопровождаются изменениями структуры электронных систем атомов. При этом во всех естественных радиоактивных рядах распада наблюдается одна и та же закономерность – значения R-функции систем электронных подоболочек, при образовании каждого нового химического элемента, последовательно увеличиваются, приближаясь к единице:

уран (0,715) ® радий (0,755) ® радон (0,782) ® свинец (0,783);
торий (0,730) ® астат (0,779) ® свинец (0,783);
протактиний (0,718) ® актиний (0,742) ® астат(0,779) ® свинец (0,783).

Совместный анализ материала, изложенного в пунктах а) - в), позволяет предполагать, что в природе существует определенный закон структурной организации системных образований, который регулирует антагонистические взаимоотношения хаоса и порядка таким образом, чтобы системные образования устойчиво функционировали в пределах центрального интервала значений N, а значения системной R-функции по мере их развития стремились к единице.

Следует отметить, что в пользу сделанного предположения свидетельствуют также экспериментальные оценки R-функции органических и лингвистических систем. – Белковые молекулы: гемоглобин человека: a -цепь аминокислот – 0,93, b -цепь – 0,98; миоглобин кита – 0,87. Одно из наиболее совершенных поэтических произведений – поэма Пушкина "Евгений Онегин": 1-е четырнадцатистишие – 0,94, 2-е четырнадцатистишие – 0,98 и т.д.

2.2. Оценка структурной организации языковых текстов

Любой языковый текст от единичного слова до объемного литературного произведения может быть представлен как закрытая система A, элементами которой являются буквы, а системными объектами B₁, B₂, …, B_N, соответственно, совокупности одинаковых букв. Структурно-статистические особенности таких лингвистических систем, в общем случае, зависят от двух факторов: грамматического строя языка и количества букв (N) используемого алфавита. Первый фактор определяет среднестатистическое соотношение системных объектов текста по количеству элементов и, как следствие, обуславливает вероятности появления отдельных букв, а второй фактор, в свою очередь, ограничивает общее число таких системных объектов. Исходя из этого, при исследовании языковых текстов естественным выглядит желание для оценки их структурной организации использовать R-функцию, которая для произвольного текста имеет вид:

.                                                                      (16)

Вместе с тем, анализируя выражение (16) с лингвистических позиций, отмечается следующее. После того, как в тексте задействованы все буквы алфавита, дальнейшее увеличение его длины
L₀ = m(A) приводит к тому, что энтропия отражения S, в соответствии с вероятностями появления букв в тексте, принимает практически постоянное значение. Следствием этого является тот факт, что R-функция текста по существу становится зависящей только от его длины и при неограниченном возрастании последней стремится к бесконечности. Отсюда следует, что при оценке структурной организации языкового текста необходимо накладывать определенные ограничения на длину оцениваемых участков с таким расчетом, чтобы влияние энтропии S на величину R-функции не было затушевано. Иначе говоря, значения энтропии S и аддитивной негэнтропии IS должны быть сопоставимы между собой. То есть, по сути дела, нужно установить соответствующий порог длины текста, функционально учитывающий как общее количество букв в алфавите, так и вероятности их появления. Очевидно, что такой пороговой величиной является длина текста, который находится в состоянии информационно-энтропийного равновесия ( R = 1 ) при задействовании всех букв алфавита. Будем называть эту длину характеристической длиной языкового текста и обозначать через . Определим ее.

Из условия получаем, что при информационно-энтропийном равновесии
I_A = 2S, откуда:

.                                                                                        (17)

В качестве примера использования формулы (17) приведем значения , полученные с ее помощью для русского, английского, немецкого, французского и испанского языков, энтропия букв которых, соответственно, равна 4,35; 4,03; 4,1; 3,96; 3,98 [ 12 ] : русский язык – 416 букв, английский – 267, немецкий – 294, французский – 242, испанский – 249. Используя теперь характеристическую длину , как скользящее окно, можно получать текстовые графики R-функции и проводить по ним сравнительный анализ структурной организации любых текстов, независимо от того на каком языке они написаны.

2.3. Социально-политические аспекты

2.3.1. Критерии президентских и парламентских выборов.

Узаконенные в настоящее время критерии регистрации кандидатов в президенты РФ (сбор 1-го млн. подписей) и получения квоты мандатов в Гос. Думе для политических партий и движений (набирание 5 % голосов на выборах) основаны на субъективных факторах жизненного опыта и интуиции лиц принимающих решения. По этому поводу идут многочисленные дискуссии, большинство участников которых принципиально сходятся в одном: 1-го млн. подписей для регистрации кандидата в президенты РФ явно недостаточно, а 5 % барьер для политических партий и движений при выборах в Гос. Думу является относительно завышенной величиной. Математический аппарат синергетической теории информации позволяет получить формализованное значение указанных критериев. Ход рассуждений при этом сводится к следующему. – Минимальное значение аддитивной негэнтропии отражения для закрытых систем, независимо от числа их элементов, составляет 1 бит (отражения), что в излагаемом контексте соответствует отражению полной совокупности избирателей через максимально возможное разнообразие политических взглядов, представлений и мнений. Исходя из этого, разумно потребовать, чтобы количество информации (негэнтропии) о полной совокупности избирателей, отраженное через ту ее часть, которая априорно поддерживает кандидата в президенты или голосует за какую-либо партию или движение, было также не менее одного бита. Иначе говоря, информационная полнота отражения всей совокупности избирателей через одну качественно обособленную часть должна быть не ниже, чем при отражении совокупности через максимальное число таких частей. В математическом отношении сказанное выражается условием:

                                                                   (18)

где: m(A) - общее число избирателей, m(B_i) - число избирателей, априорно поддерживающих i-го кандидата в президенты или голосующих за i-ю политическую партию или движение. Исходя их 106 млн. российских избирателей, согласно условию (18) получены следующие значения критериев: необходимое число подписей для регистрации кандидата в президенты РФ – 4,78 » 5,0 млн. подписей, проходной барьер для политических партий и движений при выборах в Гос. Думу – 4,51 » 4,5 % голосов.

2.3.2. К вопросу о численности парламентских партий и движений.

Не вызывает сомнений, что действительная численность политических партий и движений, баллотирующихся на выборах в Гос. Думу, должна быть репрезентативной относительно общего числа избирателей. Критерием такой репрезентативности можно считать выполнение условия дробления системы на равнозначные части, когда хаотичность ( энтропия S ) отражения системы через совокупность этих частей не превосходит его упорядоченность ( негэнтропию IS ), то есть:

.                                                                                     (19)

Из выражения (19) следует, что фактическая численность парламентских партий и движений, должна быть не ниже пороговой величины . Значение этой величины для РФ составляет 10296 » 10000 чел. Указанную пороговую величину репрезентативности качественно обособленных частей системного образования можно использовать также и для формализованного структурирования социально-политических институтов избирательной власти. Например, для того, чтобы в Гос. Думе РФ, состоящей из 450 депутатов, была зарегистрирована новая депутатская фракция, необходимо, чтобы в ее составе было не менее = 21,2 » 20 чел.

2.4. Прогнозно-геологические исследования

В практике количественного прогнозирования месторождений полезных ископаемых ключевое положение занимает задача оценки информативности признаков, как количественной характеристики их прогнозно-поисковой значимости. Одним из традиционных путей решения данной задачи является использование различных вероятностных мер, включая модификацию информационной меры Шеннона – формулу частной информации "от события к событию" [ 13 ]. Вместе с тем, как показывает анализ [ 14 ], такая методика дает неустойчивые, ситуационные значения информативности, которые могут приводить к противоречивым прогнозным заключениям в целом. Свободными от этого недостатка являются способы определения информативности признаков, основанные на их негэнтропии отражения относительно эталонных рудных объектов. Такое определение информативности признаков используется прогнозирующей системой ИНФОТ (ИНФормация и ОТражение), которая получила положительную оценку при поисках различных видов полезных ископаемых [ 15 ].

Заключение

Сделаны только первые шаги по разработке и оформлению синергетической теории информации, а также по выявлению ее взаимосвязи с другими научными дисциплинами. Подтверждением этому является тот факт, что все сказанное в статье относится только к одномерному отражению. Но, уже сейчас, как свидетельствует изложенный материал, можно говорить, что речь идет о новом научном направлении в области общей теории информации, которое, по мере своего развития, окажет неизбежное влияние как на теоретические, так и на прикладные исследования в различных предметных областях.

NB. Автор будет признателен всем, кто пришлет свои отзывы, предложения и замечания относительно изложенного материала по адресу:

Приложение

Комментарий к термину "негэнтропия"

Термин негэнтропия не имеет пока достаточно широкого распространения в научной литературе, поэтому имеет смысл остановиться на его общей интерпретации. – Уже сам факт наличия у слова энтропия отрицательной приставки нег свидетельствует о том, что за понятием негэнтропия скрывается некоторая сущность, противоположная сущности энтропии и отрицающая ее, так сказать, некая отрицательная энтропия. Первым понятие отрицательная энтропия употребил в 1945г. известный австрийский физик Э.Шредингер, который, анализируя с термодинамических позиций жизнедеятельность органического мира, пришел к выводу, что биологическим системам для своего существования необходимо извлекать из окружающей среды отрицательную энтропию, чтобы компенсировать внутреннее производство энтропии, и тем самым тормозить свое движение в сторону термодинамического равновесия, соответствующего состоянию смерти. (См.: Шредингер Э. Что такое жизнь? Точка зрения физика. М.: Атомиздат, 1972. )
Впоследствии американский физик Л.Брюллиэн, исследуя превращения (деградации) одних видов энергии в другие, для краткости отрицательную энтропию стал называть негэнтропией и ввел этот термин в теорию информации, сформулировав свой негэнтропийный принцип информации: “Информация представляет собой отрицательный вклад в энтропию” (Бриллюэн Л. Научная неопределенность и информация. М.: Мир, 1966. с.34.) Сейчас термин негэнтропия употребляется главным образом в двух значениях: как количество информации, равное разности между начальной (до получения сообщения) и конечной (после получения сообщения) энтропий, и как величина, обратная энтропии, выражающая упорядоченность материальных объектов. (См., например: Кондаков Н.И. Логический словарь-справочник. М.: Наука, 1976. .) В настоящей статье под термином негэнтропия, в общем случае, понимается информация о “чем-либо”, отраженная (воспроизведенная) через “что-либо”, и в этом отношении характеризующая отражение исследуемых объектов со стороны организованности, упорядоченности, определенности (в противоположность энтропии, как мере хаотичности, рассеянности, неопределенности). Короче говоря, в синергетической теории информации негэнтропия отражения – это отраженная информация. При этом количественная оценка негэнтропии осуществляется независимо от оценки энтропии и, более того, генетически предшествует последней. В отношении же словосочетания негэнтропия отражения следует сказать, что оно употребляется прежде всего для того, чтобы отличать негэнтропию, как меру упорядоченности отражения, от других ее интерпретаций.

Литература и примечания

1. Под системным объектом понимается качественно обособленное множество элементов в составе некоторой системы, рассматриваемое как единое целое.
2. См., например: Хартли Р.В.Л. Передача информации. В сб.: Теория информации и ее приложения. М.: Физматгиз, 1959. С. 5–35; Шеннон К. Работы по теории информации и кибернетике. М.: Изд. иностр. лит., 1963. 830с.
3. Шеннон К. Указ. соч. С. 667.
4.Урсул А.Д. Отражение и информация. М.: Мысль, 1973. 231с.; он же: Проблема информации в современной науке. М.: Наука, 1975. 288 с.
5. Советский энциклопедический словарь. М.: Сов. энциклопедия, 1989.
6. Форма выражения I_A в (4) является математическим подобием информационной меры Хартли, взятой при единичном выборе и двоичном основании логарифма (см. Хартли Р.В.Л. Указ.соч.), но принципиально отличается от нее тем, что количество символов используемого алфавита в мере Хартли является числом логарифма, а в (4) – его основанием.
7. Это является подтверждением философского заключения Урсула А.Д. о взаимоотношениях различных видов информации: “В природе, по-видимому, нет резких граней … между различными видами самой информации. Высшие виды информации “незаметно” переходят в низшие, и связь с управлением отнюдь не служит той границей, за которой уже нет информации” (Урсул А.Д. Указ. соч. 1975. С. 62. (Разрядка моя – В.В.)).
8. О необходимости установления в теории информации своих специфических законов, подобных физическим законам сохранения, говорилось еше в 50-х – 60-х годах 20-го века, но решение проблемы так и не было получено. (См., например: Харкевич А.А. Очерки общей теории связи. М.: Гостехиздат, 1955; Новик И.Б. Негэнтропия и количество информации // Вопросы философии, 1962, № 6.)
9. Основанием для такого огрубления служит тот факт, что его относительная погрешность в соответствии с числом Лошмидта N_L = 2,687*10¹⁹ 1/см³, выражающего количество молекул идеального газа, находящихся в 1см³ при нормальных условиях, составляет: для 1см³ – 2,3 %, для 1м³ – 1,7 % и т.д. В то же самое время, многие из реально существующих природных систем имеют несравненно большие размеры, что делает указанное огрубление оправданным. (Например, запасы месторождений природного газа, которые в первом приближении представляют собой изолированные системы, иногда исчисляются триллионами кубометров.)
10. Вавилов С. Физика // Под знаменем марксизма, 1935, № 1. С. 124 – 136.
11. Шеннон К. Указ. соч. С. 667.
12. Яглом А.М., Яглом И.М. Вероятность и информация. М.: Наука, 1973. 512с.
13 Вентцель Е.С. Теория вероятностей. М.: Наука, 1969. – 576с. Использование формулы информации “от события к событию” см., например в работе: Высокоостровская Е.Б., Зеленецкий Д.С. О количественной оценке перспектив территории при поисках месторождений рудных полезных ископаемых // Сов. Геология, 1968, № 8. С. 58 – 71.
14. Вяткин В.Б. К вопросу информационной оценки признаков при прогнозно-геологических исследованиях // Известия Уральского горного института. Сер.: Геология и геофизика, 1993. Вып.2. С. 21-28; он же: Информационные прогнозно-геологические антиномии. // Компьютерное обеспечение работ по созданию государственной геологической карты Российской федерации: Материалы 5-го Всероссийского совещания-семинара. - Ессентуки, 1998. С. 116-119.
15. Вяткин В.Б., Автонеев С.В. Выделение новых потенциально золоторудных площадей в пределах Краснотурьинского рудного узла с помощью системы ИНФОТ // Геологическое картографирование и прогнозно-металлогеническая оценка территорий средствами компьютерных технологий: Материалы 6-го Всероссийского совещания-семинара по компьютерным технологиям – Красноярск, 1999. С.175-178; Вяткин В.Б. Страшненко Г.И., Мельник В.В. Прогнозная оценка Сакмарского кварценосного района с помощью системы ИНФОТ // Геологическое картографирование и прогнозно-металлогеническая оценка территорий средствами компьютерных технологий: Материалы 6-го Всероссийского совещания-семинара по компьютерным технологиям. Красноярск, 1999. С.178-181.