 |
||
Каталог >> ИИ >> ИНФОРМОДИНАМИЧЕСКИЕ ОСНОВЫ ОРГАНИЗАЦИИ УПРАВЛЕНИЯ ПРЕДПРИЯТИЯМИ И ХОЛДИНГОВЫМИ КОМПАНИЯМИ |
Глава 2. Моделирование для управляющего
2.1. Направления и подходы к моделированию
Приступая к исполнению своих управляющих обязанностей, каждый подготовленный руководитель той или иной компании, безусловно, знает некоторое количество подходов к моделированию производственных ситуаций, оптимизации принятия решений и альтернативному выбору в случае возможных коллизий.
Но, по опыту общения с этими самыми управленцами, всем нам ясно, что их подготовка в области управления ограничивается изучением некоторого набора примеров применения различных методов моделирования в ситуациях, когда обстановка может быть алгоритмизирована. Это не их вина. Ничего другого существующая технология моделирования предложить не может, включая и так называемые интеллектуальные технологии моделирования [38].
Последнее вполне естественно, ибо ничем другим математическое моделирование (моделирование на кибернетическом уровне, уровне использования не присущих Природе абстракций) быть не может. Хорошо, когда его применяют для целей разработки и анализа кибернетических систем. Но у нас речь идет о системах куда более сложных.
Для того, чтобы в какой-то мере разобраться со сложившейся ситуацией и найти в ней приемлемое решение, не впасть в постановочный тупик при организации управления, надо изучить и сравнить множество современных подходов, прежде всего, к моделированию как к таковому. Здесь для управленца первым препятствием является множество дополнительных отличительных определений вариантов моделирования, разобраться в конечной сущности каждого из которых не всегда сможет даже очень квалифицированный менеджер.
Перечислим ряд вариантов организации моделирующих подходов, встречающихся в литературе: математическое моделирование, алгоритмическое моделирование, имитационное, физическое, моделирование на сплошных средах (электрическое моделирование), вероятностное, статистическое, моделирование с переменными структурами (статическое и динамическое). Ну а уж натурное и полунатурное моделирование все производственники знают изначально.
С другой стороны существует деление моделей по области моделирования (см., например, [41] и др.) – модели экономические, предприятий, военных игр и ситуаций, другие. Здесь терминологическое поле практически неограниченно. В лучшем случае это описание практической реализации моделей из предыдущего списка. К сожалению, иногда постановка моделирования настолько спрятана за терминологией и собственными особенностями области моделирования, что выявление использованного подхода становится затруднительным.
И с третьей стороны – существуют попытки создания обобщенной теории моделей (Сегодня мы можем указать как минимум три направления, претендующие на понятие метатеории в рассматриваемой нами области. Это общая теория систем, поскольку системами мы здесь занимаемся явно, общая теория управления, ибо все системы существуют только как процессы их возникновения, существования при поддержании их некоторым механизмом обеспечения их динамической устойчивости, и общая теория моделей, как частный случай существования в условиях ограничений обобщенной задачи управления. Если уж заниматься математическим подходом к управлению, то частные построения должны быть подмножествами общих теорий, а не паллиативами, ожидающими своей смерти после прихода обобщающих построений). Однако реально пока достаточно признать наличие двух основных направлений.
Первое из них ориентируется на преимущественно математическую сторону и выявление опыта специалистов проблемных областей для более полного использования методов математики, как при построении математических моделей, так и при организации вычислительного эксперимента.
Фактически проблемный специалист в этом подходе является не более чем консультантом для профессионального математика. Более того, даже тестирование разработанного программного обеспечения не отдается на откуп программистов, а проводится с позиций обеспечения требований математики
(Некоторые специалисты называют это “подходом А.А.Самарского”).Так называемая “новая информационная технология моделирования” в противоположность первому подходу ориентирована на конечного пользователя, которому отводится непосредственная роль разработчика модели. Упор здесь делается на создание языков представления моделей, ориентированных на непрограммирующего пользователя и инструментальных средств “с элементами искусственного интеллекта”.
Считается, что это направление рассчитано на внедрение методов моделирования в среду непрограммирующих конечных пользователей и позволяет исключить программиста, а в некоторых случаях и системного аналитика при реализации вычислительного эксперимента
(Это направление связывают с работами школы Г.С.Поспелова).Достаточно ясно, что в первом случае будет получено строгое решение, строгость которого обеспечена проработанностью начальных ограничений. Это решение, которому вполне можно доверять, если его граничные и начальные условия когда-нибудь будут совпадать с реалиями моделируемого объекта или процесса, и которое откажется дать вам какие-либо гарантии своей правильности, если таковых условий не будет.
Во втором случае предлагается далеко не строгое решение, доверять которому можно не всегда и только после его косвенных проверок любыми мыслимыми способами (экспертным, например).
Зато такого рода результаты в общем случае куда меньше зависят от колебания начальных условий постановки задачи, менее чувствительны к граничным условиям просто потому, что так называемые “методы искусственного интеллекта” в существующей постановке дают возможность конечному пользователю сформулировать задачу не столько строго, сколько многовариантно, с последующим выбором того, что ему по какой-либо причине понравится.
Читателю уже ясно, что эти подходы могут быть сравнены между собой как САУ и АСУ с присущими им недостатками при их применении для управления открытыми системами. Все способы коррекции этих недостатков, называемые “переходом к интеллектуальному управлению” дают в организационном управлении не больший выигрыш, чем в обычном. И только подходы уровня теории интеллектуальных систем управления (ИСУ), с более конструктивным пониманием интеллектуальности [13,14,15], дают некоторую надежду на решение этой задачи в будущем
(Коррекция для результатов математических расчетов для систем организационного управления может осуществляться по двум направлениям: коррекция принятия решений за счет использования различных методов привнесения извне (от человека или эвристического “накапливающего знание” алгоритма”) компенсации погрешностей использования функциональной модели организации; принципиальная замена в системе управления понятия “автоматическая” на понятие “автоматизированная” система (АСУ), т.е. включающая в себя оптимизационные алгоритмы прикладной математики и человека как устройство для принятия окончательных решений.Лучшим вариантом сегодня представляется автоматическое (без участия человека) принятие решений за счет использования систем с самоструктурирующимися базами, что является предметом прикладной теории ИСУ. В [15] под ИСУ понимается направление, связанное с организацией управления в сложных системах, ориентированное на базы знания, формируемые в процессе создания интеллектуальной системы и обеспечивающее самостоятельное принятие системой управляющих решений без использования в этом акте привносимой человеком информации. Это означает не только самостоятельную область существования прикладной теории ИСУ, но и определенную смысловую нагрузку, которую эта теория возлагает на понятие интеллектуальности, восприятие ее не “образной метафорой”, но в полном соответствии с ее классическим, энциклопедическим определением.).
Теперь мы имеем достаточно сведений для правомерного перехода к сравнительному рассмотрению ряда традиционных подходов, используемых в общепринятых постановках задач организационного управления.
2.2. Математическое моделирование
2.2.1. Общепостановочный аспект использования
математического моделирования для целей оптимизации
результатов организационного управления
Математическое моделирование настолько давно и широко распространено, столь часто описано в солидных книгах и использовано на практике, что даже сама мысль показать его практическую неприменимость в значительном числе задач организационного управления сложными объектами кажется кощунственной.
И, тем не менее, разделим все оптимизационные задачи на два класса по признаку управления на реальном объекте на основе известных и не известных, но реально существующих параметров и характеристик самих этих объектов и окружающего их внешнего мира, и управления для принятия решений о перспективных возможностях объекта на некотором отдаленном отрезке времени (задача перспективного планирования), когда все, что может быть известно об объекте, достоверно описывается только тем, что удалось предположить, а остального просто еще не существует.
Для первого случая математическое моделирование – абсолютная абстракция и достоверность получаемых на ее основе результатов не более чем попытка совмещения виртуального мира модели с реальным миром объекта.
Во втором случае виртуальная модель совмещается с виртуальным миром. Трудно сказать о ее реальной адекватности тому реальному миру, который догонит ее во времени, но в момент моделирования у нас просто ничего больше нет, и утверждение о некоторой адекватности такого моделирования задаче перспективного планирования достаточно обоснованно
(Строго говоря, когда ничего кроме модели еще не существующего будущего нет, трудно требовать ее адекватности чему бы то ни было, кроме экспертной оценки разработчика).Нет, не плохо само математическое моделирование. Нет в нем самом, в пределах его соглашений, ошибок и неправильных подходов. Речь совсем не об этом, а о его использовании для решения задач, для которых оно не предназначено и не предназначалось никогда – задач, где воля управленца, сопротивление среды и сила привходящих обстоятельств всегда превышают по своей значимости любую совокупность математических критериев и ограничительных условий оптимизации.
Вспомним классический пример разработки автоматизированной системы управления. Прикладные математики решили оптимизационную задачу минимизации затрат на перевозки в некоторой автотранспортной организации. Было учтено все, включая не только минимизацию пути, но и информацию о состоянии дорог, износе шин (важнейший показатель для автомобилистов), ремонте и поломках машин, ведущих к необходимости изменения плана перевозок, даже расположение пунктов ГАИ. Ожидались более чем значительные прибыли от результатов эксплуатации системы.
В результате практических испытаний затраты повысились! Почему? Да потому, что оплата водителей всегда зависит от километража пробега. Они стали просто простаивать на дорогах, изменять показания спидометров, ездить объездными путями – все, что угодно, только не то, что замышлялось. Не учли важное ограничение? Нет, забыли, куда ведет любая оптимизация, и что она требует, кроме всего прочего, для своего внедрения жесточайшего порядка не только “до”, но и после внедрения.
Ясно, что любая оптимизация, а математическая на моделях – в первую очередь, ведет к интенсификации труда, к отъему у рабочего (цеха, завода, предприятия, главка, министерства) его “подкожных резервов” - скрытых от вышестоящего руководства способов получения больших доходов (меньших объемов плановых заданий, больших процентов при распределении финансов) за меньший труд.
Если мы забудем о красивых сказках времен социализма об освобождении труда (Бихевиоризм в его современном понимании мы еще затронем ниже) и примем доктрину его принудительной интенсификации за счет разработки оптимального управления (а на что, в конечном счете, направлено управление на предприятии, в холдинге, корпорации, министерстве?), то и тогда результат применения методов математического моделирования будет достаточно неожиданным, во всех случаях, кроме разработки чисто кибернетических систем.
Речь идет здесь о том, что даже с надсмотрщиком и с кнутом времен рабовладения заставить шоферов работать по новым правилам не удастся никому. Даже если их всех уволить, набрать штрейкбрехеров, вызвать автомобильную роту из соседнего полка – задача решена не будет. Для элементарного доказательства этого вспомним постановление сталинских времен “О повышении норм выработки и снижении расценок”. Вспомните, в какое количество лагерей вылилась реализация этого постановления, хотя, строго говоря, на уровне математического моделирования и некоторой оптимизации (например, по критерию срочной необходимости мировой революции) это постановление было вполне обоснованным и даже вполне реализуемым
(Если, например, убрать из рассмотрения такой параметр, как “качество жизни” исполнителей, что вполне успешно делали в те времена. Но попробуйте и сегодня найти этот параметр в какой-либо экономической оптимизационной задаче. Ссылки на социальные модели говорят только об одном – модельное замыкание представления объектов распространяется не только на ограничение “параметров по конкретной задаче”, но и на ограничение задачи, ее отстранение от областей, формально занятых другими науками, но, тем не менее, более чем важных для ее представления.).Наши деды прекрасно понимали, что оптимизация бывает математическая, а бывает действенная. Что такое, в своей изначальной форме, соцобязательство и соцсоревнование? Форма принудительной интенсификации труда. Во что это вылилось при менталитете нашего народа? В перевод хорошей бумаги на описание того, что уже сделано, либо и делать никогда не придется за ненадобностью.
Кому этого мало – пусть вспомнят А.Стаханова, П.Ангелину и других наших “героев”, да не столько их самих, сколько показательные примеры организации власть имущими оптимального управления в социальной и производственной сферах. Все то же самое распространяется и на верхние уровни организационной иерархии, будь то экономика, военное строительство или любое другое.
2.2.2. Основы математического моделирования
для задач оптимального управления
Рассмотрим, что же реально может предложить нам математическое моделирование для решения практических задач в случае, если мы закроем глаза на все сказанное в п.2.2.1.
Не будем претендовать на исчерпывающий список конкретных задач, ограничимся только главными направлениями, которые может найти любой управленец, изучая классический курс прикладной математики
(Кибернетика, тщательно пытавшаяся вобрать в себя основы прикладной математики, тихо ушла и из школьных учебников, и из Академии наук, заменив себя информатикой, которая сегодня в общераспространенной и даже научной литературе еще более не определена, чем кибернетика. А оптимизация на моделях для организационного управления как существовала, так и существует).Вряд ли мы можем представить себе сегодня руководителя крупного предприятия или холдинга, имеющего специальное математическое образование. Скорее всего, это специалист либо с профильным образованием по тематике производимых работ, либо с образованием типа “экономика и менеджмент”. Поэтому небольшой курс математического моделирования для задач управления ему будет полезен в ключе изложения, учитывающем его профессиональные интересы.
Для сокращения потерь времени на освоение этого курса построим его как компиляцию из хороших учебников 70-80-х годов, когда “всеобщая компьютеризация” еще не мешала готовить математически грамотных специалистов. И это не пустая сентенция, а вполне обоснованный вывод многих преподавателей, еще имеющих возможность сравнить прикладную математическую подготовку студентов технических вузов до начала компьютерной эры и современного периода.
Этапы цикла управления. Начнем с традиционного утверждения о четырех этапах, характерных для любого процесса управления: появление цели, оценка ситуации, принятие решения и исполнение принятого решения. Ответить на вопрос о появлении (формировании) цели в пределах математического представления невозможно, поэтому первый этап обычно исключается из рассмотрения, и управление считается начинающимся сразу со второго этапа
(Ясно, что это первый шаг к полному замыканию управляемого объекта).Различные виды задач оптимального управления отличаются друг от друга способом и последовательностью выполнения этих этапов.
Виды задач управления.
Если механизмы сбора информации и исполнения принятого решения отработаны так, что они ясны при осуществлении процесса управления, то это одноэтапные или одношаговые задачи принятия решений. В действительности чаще всего все этапы процесса управления находятся в тесной взаимосвязи, и этап принятия решения требует рассмотрения способов его реализации. В подобных случаях процесс управления разбивается на несколько последовательных шагов, причем решение каждого шага зависит от результатов шага предыдущего. Такие процессы называют многошаговыми процессами принятия решений.
Кроме редких самоочевидных случаев разбиения многошагового процесса на логически очевидные шаги, гораздо чаще такое разбиение оказывается самостоятельной сложной задачей. В пределе, при теоретически бесконечном числе шагов, мы получаем непрерывный динамический процесс управления
.Дополнительные трудности обеспечивают разнообразные внешние факторы, совокупность которых можно называть влиянием внешнего мира. В условиях кибернетического подхода всегда требуется указывать точное значение (измерение) этих воздействий. Кроме того, в реальности решение необходимо принимать в условиях, когда информация о сложившейся ситуации или недостаточна или искажена. Такая задача получила название задачи принятия решений в условиях неопределенности
(Не надо думать, что это совсем неопределенная неопределенность. Совсем нет. К ней надо без особых на то оснований приписывать некоторые законы и предположения, называя их статистически значимыми. Иначе о математической постановке задачи принятия решений здесь и речи быть не может.).Понятие об исследовании операций.
Для учета специфики задач управления, связанных с деятельностью крупных промышленных предприятий выделяется еще один класс задач управления – задачи организационно-управленческого характера
.Разработкой методов решения таких задач занимается дисциплина, получившая название исследование операций. В ней под операцией понимается некоторое организационное мероприятие, проведение которого преследует определенную четко сформулированную цель управления тем или иным ресурсом.
Такого рода задачи в первую очередь характерны для математического моделирования в интересах крупных предприятий и холдингов. Каждое подразделение крупной организации выполняет определенную часть общей работы, руководствуясь общими целями предприятия. Однако у каждого специализированного подразделения возникают и свои собственные цели. Все эти цели не только не согласуются, но по сути потребностей многопрофильного производственного процесса неизбежно противоречат друг другу.
В качестве простейшего примера обычно предлагается рассмотрение весьма показательной задачи обеспечения предприятия запасами. Отдельное подразделение может быть заинтересовано в значительном увеличении запасов на складе (или вложении ресурсов в свое развитие). Но при ограниченном объеме складских помещений (ограничении суммарного ресурса компании) это приводит к снижению запасов для других подразделений (снижению выпуска другой продукции).
В результате возникает задача организационно-управленческого типа – выработка такой стратегии в отношении запасов (ресурсов), которая была бы наиболее благоприятна для всей компании в целом. При решении организационно-управленческих задач подобного рода ставится задача согласования целей отдельных подразделений. Считается, что принятие не лучших решений может приносить ущерб и поэтому при решении организационно-управленческих задач недопустимо базироваться только на личном опыте и здравом смысле.
В литературе указывается, что в таких ситуациях необходимо применение научных методов. Как давно уже ясно нашему читателю, беда не в том, что слишком сложна задача, и слишком трудно сформулировать критерии исследования операций.
Неразрешимая трудность критериального управления заключается в том, что подразделения “по факту смысла своего существования” будут до конца препятствовать оптимальному не для них решению, и руководству неизбежно приходится переходить к управлению волевому. Но для волевого управления рассмотренный выше цикл организации принятия решений бессмыслен, а иного оптимизационное управление предложить не может.
Поэтому в той же литературе указывается, что принятие окончательного решения всегда относится к компетенции ответственного лица, администратора, наделенного соответствующими правами, и выходит за рамки исследования операций. Но там же говорится, что исследование операций представляет собой научное направление, собственной целью которого являются разработка методов анализа целенаправленных действий (операций) и объективная сравнительная оценка возможных решений
(Предоставляем читателю самостоятельно определить, в чем же состоит объективность указанной сравнительной оценки и вспомнить, исходя из своего собственного опыта, когда в последний раз у него было желание решать такого рода задачи о распределении ресурсов чисто оптимизационными методами. Заодно можно еще раз задуматься о соответствии математического подхода и реалий окружающего нас мира.).Возникло же это направление, судя по литературным источникам, как задача ПВО английской армии. Действительно, какой самолет противника уничтожать в первую очередь, и какой во вторую – это настоящая задача исследования операций, где человек готов полностью и без сомнений довериться хорошо отлаженному алгоритму. Здесь все понятно – человеку никогда не решить такую задачу быстрее и лучше машины. Хорошо поставленной кибернетической задаче должно соответствовать хорошее математическое решение. Но организационное управление – не кибернетическая задача.
Критерий качества управления.
Задачу управления нам всегда предлагают рассматривать как математическую задачу. Однако, в отличие от многих других математических задач, она допускает не одно решение, а множество различных решений, вернее – множество различных процедур решений
(Фактически задача управления дает нам как минимум два направления, выбор которых необходим уже на начальной стадии ее постановки. Первое из них – работа с варьируемыми параметрами выбранной процедуры решения задачи. Второе – выбор той или иной процедуры решения. Достаточно ясно, что проделав и то и другое, исследователь в общем случае не получит совпадающие множества решений.).Поставить задачу управления как задачу хотя бы одного из возможных способов достижения цели обычно считается недостаточным. Если мы не имеем ограничений на время принятия решения, информацию и обрабатывающие ресурсы, то всегда будем стремиться решить добавочную задачу – выбрать из возможного множества решений лучшее по какой-либо совокупности критериев их сравнения.
Математическое выражение, дающее количественную оценку степени выполнения наложенных на способ управления требований, называется критерием качества управления. Наиболее предпочтительным или оптимальным способом управления будет такой, при котором критерий качества управления достигает минимального (максимального) значения.
При выборе, например, режима полета за критерий качества управления можно принять или выражение для количества топлива, расходуемого на единицу пути, или путь, проходимый за счет единицы топлива. Наиболее экономичному, т.е. оптимальному режиму будет соответствовать или минимальное, или максимальное значение критерия качества управления
(Пример взят из довольно известного учебника. Предлагаем сравнить его с изложенной выше историей с оптимизацией затрат автоколонны. Остается только надеяться, что трудовая дисциплина летного состава пока еще выше дисциплины наземных транспортников, хотя летные часы первым нужны не менее, чем километраж шоферам.).Ограничения управления. Нет и не может быть в реальном мире и даже в его модельных конструкциях управлений, если на характер движения системы не наложено никаких ограничений. Принятое решение, принятое управление обладает последействием и это заметно не только при торможении автомобиля, но, в большей степени, в задачах снабжения, планирования, управления большими организациями.
В общем случае имеется два вида ограничений на выбор способа управления. Ограничениями первого вида являются законы Природы, в соответствии с которыми существует управляемая система (Предприятия и холдинги не являются исключением из этого правила. Порожденные необходимостью существования природных объектов – людей, они сами, как мы уже указывали, ничуть не менее природные образования, чем образующие их объекты. ). При математической формулировке задачи управления эти ограничения представляются обычно алгебраическими, дифференциальными или разностными уравнениями объекта управления, и их часто называют уравнениями связи.
Второй вид ограничений вызван ограниченностью ресурсов, используемых при управлении, или иных величин, которые в силу физических особенностей той или иной системы не могут или не должны превосходить некоторых пределов. Математически ограничения этого вида выражаются обычно в виде систем алгебраических уравнений или неравенств, связывающих переменные, описывающие состояние системы.
Постановка задачи оптимального управления. Считается, что в постановочном смысле не имеет значения, чем именно мы собираемся управлять, если речь идет об оптимальном управлении: формулировка оптимального может быть дана только в математическом смысле, без апелляции к смыслу реальной задачи, и задачу управления можно считать сформулированной если:
Способ управления, который удовлетворяет всем поставленным ограничениям и обращает в минимум (максимум) критерий качества управления, называется оптимальным управлением.
Как вывод по этой части рассмотрения проблемы математического моделирования для задач управления следует, что любой средний управленец в принципе и без введенных выше понятий и определений делает все “правильно”, но с учетом недоступных никакому математическому представлению “привходящих обстоятельств”. Когда же расчеты по модели становятся критическими, т.е. приходится принимать решения внешне весьма пригодные для математического обсчета (например, принятие решения о ресурсном обеспечении конкурирующих частей организации), решение все равно предлагается принимать человеку из-за необходимости учета “привходящих обстоятельств”.
2.2.3. Описание объекта управления
Теперь рассмотрим, что дает управленцу составление математического описания объекта управления. В литературе обычно приводится примерно следующее утверждение: “То обстоятельство, что закономерности, которым подчиняются процессы управления, являются общими для объектов любой физической природы, позволяет рассматривать общую структуру и предлагать общее математическое описание процесса управления, будь то управление техническим устройством, производственным предприятием, экономической, биологической или, скажем, социальной системой”.
Представляется, что уже здесь происходит подмена так называемого “объема понятий”. Приведенные выше рассуждения, общие для всех постановок задач управления, ведут читателя к тщательно завуалированной подмене – открытые природные образованья, собственный язык которых из-за его контекстной зависимости на порядки сложнее математического, фактически предлагается считать эквивалентными по управлению техническим устройствам. Отметим этот факт и продолжим рассмотрение традиционного подхода.
Обычно через переменную
x обозначают состояние объекта управления. В большинстве случаев состояние x характеризуется некоторым набором компонент x1,…,xN , представляющих собой количественные характеристики, количественные описания состояния x. Соответственно во всех случаях состояние объекта управления будет описываться многомерной, т.е. векторной переменной x, компонентами которой будут величины xi:x = (x1,…,xN).
Теперь переменную
x можно назвать переменной или вектором состояния объекта управления.Величины
xi могут изменяться непрерывно в некотором диапазоне значений или принимать конечное множество значений. Для простоты записи (и без каких-либо сущностных потерь) рассмотрим математическую запись последнего варианта. При нем величина x будет также принимать конечное множество значений и ее k-е значение обозначают черезx(k) = (x1(k),…,xN(k)), k = 1,…,n.
Тогда множество
X = {x(1), ,x(n)}
будет представлять собой пространство возможных состояний объекта управления. Иногда пространство
X называют пространством решений, подчеркивая тем самым, что выбор некоторого конкретного состояния x из множества X представляет собой возможное решение задачи управления.Ясно, что на значения
xi накладываются различные ограничения, вид которых мы уже указывали выше – например, система алгебраических уравнений или неравенств.Совершенно аналогично вводится конечное или бесконечное (обычно сводимое для простоты к конечному) множество
?
= {?(1), … , ?(h)},называемое уже не пространством состояний объекта, а пространством состояний природы.
Дополнительно здесь целесообразно указывать, что вместо точного знания состояния природы
? во многих случаях приходится ограничиваться лишь знанием вероятностей ?(?) различных состояний природы во множестве ?.Как читатель уже догадался, все то же самое пишут и про управляющее воздействие или просто управление. А именно: обычно приходится использовать управление, состоящее из нескольких управляющих воздействий
ui, так что управление u представляет собой в общем случае многомерную величинуu = (u1,…,uR).
И точно также множество допустимых управлений
u может быть бесконечным, а может быть и конечным, тогдаU = {u(1), … , u(r)}.
Под действие сигналов управления
u объект управления изменяет свое состояние. Характер происходящих при этом процессов определяется скоростью изменения переменной состояния объекта![]() = (
= (![]() 1,…,
1,…, ![]()
где
Для динамических систем, в которых физические процессы протекают непрерывно во времени, скорости
![]()
где величины
сi (i = 1,…,N) характеризуют начальное состояние объекта управления.Вот, собственно говоря, и вся начальная математика, практически одно и то же выражение, повторенное несколько раз. Этого достаточно любому управленцу для понимания того, как работает математический аппарат оптимизации и критериального управления. Безусловно, в профессиональной математической литературе все будет изложено полнее и строже, но суть останется неизменной.
Здесь хочется напомнить известное изречение математика времен становления Винеровской кибернетики Г.Герхарда: “Математика – наука, в которой издавна происходит прогрессирующая формализация, т.е. замена разговорного языка математическими символами”. Выше мы получили хороший образец этого прогресса – прогресса мира технического, свойства которого впрямую и без должного основания переносятся на “мир природный”.
Но и с языками компьютера дела обстоят подобным образом. Вместо привычного естественного языка человека для общения с компьютером мы должны изучать язык, доступный именно ему, а не наоборот; вместо собственного языка должны думать и управлять на основе выводов из изложенных выше математических построений, что совсем не просто для человека.
Поэтому в обоих случаях между задачей и принятием решения стоит посредник – программист или аналогичный аналитик-расчетчик, ибо ни один руководитель никогда не будет иметь времени заниматься такими делами самостоятельно. Беда опять же не в этом, неприятности заключаются в том, что только математик – разработчик задачи знает, какие ограничения реально описаны той самой системой алгебраических уравнений или неравенств, но он не знает и не может знать, достаточно ли это и какие именно числовые ограничения реально представляет себе руководитель. Что же касается нечисловых ограничений, то здесь он вообще бессилен, а для планирования руководства организацией такого рода условия абсолютно неизбежны
(Вспоминается достаточно серьезное совещание, где рассматривался сетевой график сложного проекта, разработанный группой профессиональных прикладных математиков. Любой сетевой график имеет критический путь, соответствующий минимально необходимому сроку проведения работ. Генеральный конструктор, точно знающий, когда реально с него спросят за выполнение проекта, остался недоволен его расчетной продолжительностью и приказал сократить критический путь почти вдвое.Ничего страшного не случилось. Получив директивное указание, расчетчики прекрасно справились с коррекцией, и проект был запланирован для выполнения в указанные сроки. Оптимизация пошла по пути, описанному в п. 2.2.1. Нам кажется, что этот пример достаточно откровенно иллюстрирует проблему применения математического моделирования и оптимизации для реальных сложных проектов и предприятий.).
Обсуждение практических типовых направлений постановки и решения задач управления можно найти во множестве публикаций, построенных по одной схеме – много и подробно о том, как построить и правильно использовать возможности того или иного приема постановки и решения задачи и мало и очень скромно – о реальных не математических ограничениях их применимости.
Можно встретить и примеры, когда задача, скажем, линейного программирования дает достаточно разные результаты при решении ее как целочисленной и без учета этого условия, но с последующим математически правильным округлением. Конечно, можно показать (что практически никогда не делается за ненадобностью такого доказательства), что вроде бы одинаковые начальные и граничные условия в этих случаях приводят к разным результатам расчетов, но практику от этого не легче. Если он знает априорно, какое решение его устраивает, то выбор ясен. А если не знает? Как решать будем: целочисленно или с округлением?
Часто одну и ту же задачу можно сформулировать и как задачу обслуживания, и как задачу планирования, и как задачу одношаговую, и как задачу многошаговую, а уж предположения о законах распределения некоторых входных параметров часто в принципе не имеют возможности опираться на какие-либо статистики.
Но главным является скорее не искусство выбора и подбора, а то, что все эти задачи являются задачами на поиск экстремума в некотором специально конструируемом пространстве признаков.
Если эти признаки чисто количественные, то и тогда мы не имеем никаких априорных доказательств или подсказок для выбора системы измерения в этом пространстве при математическом поиске экстремальных значений. Ну а если это признаки качественные, или просто сравнительные по иерархии, без чего в реальной жизни не обходится ни одно решение, тогда как?
2.2.
4. Формализация процедур планированияРассмотрим задачи управления, имеющие смысл в оптимизационной постановке, задачи перспективного планирования. Мы уже говорили о постановочной корректности таких задач, связанной с отсутствием непрогнозируемых возмущений (В контексте перспективного планирования постановочная корректность математического прогнозирования определяется следующим.
В обычных оптимизационных постановках некоторый объект оптимизируется с модельными ограничениями для существования в среде, которая считается неизменной на расчетный период и реально существует как открытая система.
Перспективное планирование нсходит либо из концепции “внутриобъектного планирования”, когда параметры среды вообще не влияют на объект, либо из предположения о тенденциях изменения внешнего, относительно объекта, мира. В этом случае окружающая среда для рассматриваемого объекта является столь же модельной, как и сам объект. В результате два равно достоверных (или недостоверных) математических предположений о моделях объекта и среды являются единственным доступным нам представлением будущего, любое уточнение которого будет являться также не более чем моделью.). Изначально отметим, что существуют два принципиально разных подхода к планированию научно-производственной деятельности:
-
долгосрочное планирование от прошлого к будущему для оценки перспектив производства некоторой продукции, находящейся в стадии насыщения рынка и отличающейся отработанной стабильностью технологических процессов и характеристик;-
стратегическое планирование от будущего к настоящему для процессов обновления продукции, создания новых или реорганизации существующих производств.Часто перспективное планирование рассматривается в обобщенном подходе как планирование стратегическое, для которого исторически выделяют три этапа его развития.
Первый этап:
до середины 60-х годов – стратегическое планирование эквивалентно долгосрочному планированию, при котором конечные цели заданы в виде требуемых значений ряда технико-экономических показателей; прогноз будущего осуществлялся путем моделирования.Второй этап: во второй половине 60-х – начале 70-х годов
– стратегическое планирование эквивалентно хозяйственному планированию, при котором структурные единицы действуют на коммерческой основе и оцениваются по прибыли; прогноз будущего опирается на анализ внешней среды (маркетинг рынков сбыта) и на выработанную по его результатам стратегию диверсификации.Третий этап: с конца 70-х годов
– стратегическое планирование основывается на интеграции независимых планов развития структурных единиц в стратегию развития фирмы, определяющую общие цели, приоритеты в распределении ресурсов, главные направления инвестиций; неопределенность условий деятельности требует большого объема организационной и исследовательской работы на базе новых информационных технологий.Сегодня стратегическое планирование предназначено для формулирования целей, проблем и задач развития, выбора способов и организации достижения этих целей. В работе [
16] дана характеристика технологии стратегического планирования, включающего стадии анализа, выбора собственно стратегии развития и путей ее реализации, указаны варианты целей, инструментальные средства и сущность принимаемых решений на каждой стадии.Опыт стратегического реформирования отечественных научно-производственных объединений с использованием ряда формализованных и эвристических процедур обобщен в [
2,17] . В частности там указывается, что применительно к приборостроительным предприятиям, создающим радиоэлектронные комплексы (РЭК), можно выделить следующие направления и уровни совершенствования и развития основной деятельности:-
совершенствование механизмов управления научно - производственной деятельностью, принципов построения и функционирования РЭК, процессов их проектирования и производства; автоматизация существующих методов проведения проектно-конструкторских работ, технической подготовки производства и технологических процессов, автоматизация планирования, учета и анализа результатов основной деятельности, автоматизация исследований и испытаний при системном проектировании РЭК.Второе направление как фактор стратегического развития обычно срабатывает только при значительных разовых затратах, причем при охвате не одного-двух подразделений, но только в масштабах всего предприятия или фирмы. При таком подходе расчеты могут базироваться на том же оптимизационном подходе, где он справедлив настолько, насколько можно спрогнозировать “частное, конкретное будущее” в отвязке от реальных внешних воздействий.
Первое же направление, не исключающее автоматизации, но основанное на изменениях основных методов и принципов работы, рассматриваемое в ключе планирования стратегии развития некоторого предприятия и с учетом примеч. 31, вполне может адекватно обладать тем или иным математическим аппаратом из числа рассмотренных выше или, например тем, вариант которого мы сейчас рассмотрим.
Начнем с того, что процесс освоения промышленным предприятием новой продукции связан с изменением его облика, включая технологию работ, состав оборудования, квалификацию персонала. Соответствующие мероприятия объединяют в программу технического развития, опирающуюся на выбранные типовые технические решения и способы рационального распределения ресурсов по направлениям [
18] .Для реализации новой технологии работ необходимы технические средства (станки, приборы, стенды и т.п.) с определенными значениями технических и эксплуатационных характеристик. При этом задача сводится к выбору типа и состава средств, которые обеспечивают выполнение некоторых требований
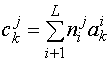 ,
,
где:
![]() -
-
k
– номер требования суммарной характеристики оборудования.Схема решения такой задачи включает следующую последовательность операций:
1)
сбор исходных данных о наборах характеристик устройств2)
генерация таблиц3)
расчет таблицы значенийЕсли решение не удается найти, следует расширить состав типов устройств, увеличить число рассматриваемых вариантов или ослабить требования.
Далее представляется полезным рассмотреть схемы согласования программы научно-производственной деятельности (НПД) и технического развития предприятия (рис. 2.1).
Целью совместного формирования программ основной деятельности и развития предприятия является приведение в соответствие портфеля заказов и технологических паспортов структурных единиц при оптимизации прибыли за заданный период.
Процедура связана с выполнением расчетов по предложенной методике на основании одной из двух схем, указанных на рис. 2.
1:-
при отсутствии заранее заданной программы НПД (планирование на большой период) используют первую схему, исходя из бизнес-плана основной деятельности и ее диверсификации, сформированного по результатам стратегических и маркетинговых исследований;-
при наличии программы НПД в виде портфеля гарантированных заказов со сметами используют вторую схему, основанную на алгоритме многотемного планирования работ.В целом методика формирования программ основной деятельности и развития предприятия сводится к следующему. Исходным являются технологические “паспорта” структурных единиц предприятия, характеризующие их мощности, освоенные технологии и нормативные модели работ.
1)
При заданном портфеле заказов (обычно на период 2-5 лет):-
на основе алгоритма многотемного планирования [ 19] с учетом технологических паспортов формируют план выполнения портфеля заказов, т.е. вариант программы НПД, обеспечивающий максимальную загрузку структурных единиц, и оценивают ожидаемую прибыль (ущерб);-
определив требования к техническим средствам, улучшающим технологические паспорта максимально загруженных структурных единиц, решают задачу выбора оптимального типа и состава таких средств и оценивают предполагаемые затраты на их приобретение, установку и эксплуатацию;
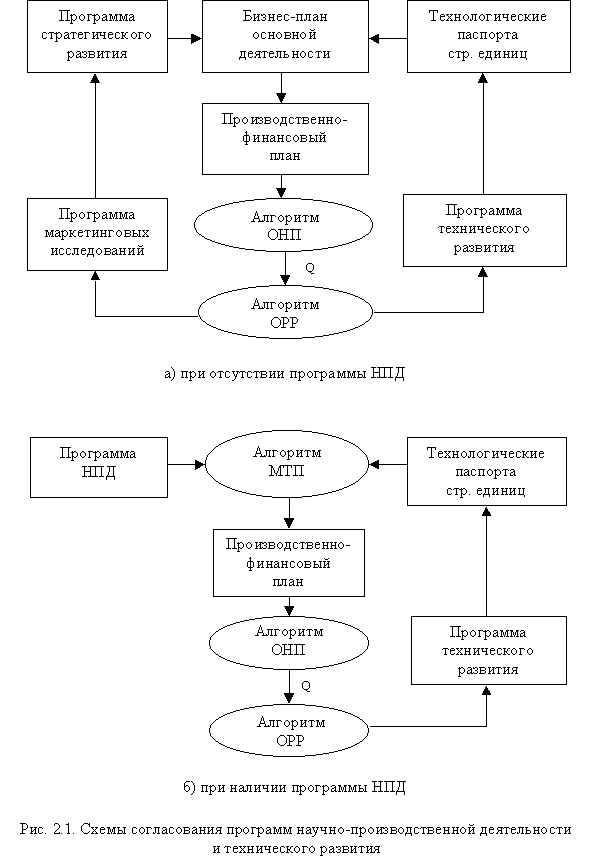
-
формируют второй вариант программы НПД с учетом новых характеристик технологических паспортов и оценивают ожидаемую прибыль.Рост ожидаемой прибыли должен быть больше предполагаемых затрат на развитие.
2)
При неопределенности портфеля заказов (возрастающей с увеличением планового периода):-
определяют с учетом технологических паспортов предельно допустимую программу НПД на этот период и соответствующую прибыль от ее выполнения;-
на основе “магистрального решения” задачи о норме прибыли, направляемой на воспроизводство основных фондов [ 20] , определяют масштабы требуемых затрат на развитие предприятия;-
исходя из предполагаемых затрат на развитие и принятых гипотез о зависимости между величиной затрат и значением показателя конкретного направления (включая развитие материально-технической базы, повышение профессионального уровня персонала, совершенствование механизмов управления, маркетинг) решают задачу оптимального распределения ресурсов по всем направлениям и определяют ожидаемые характеристики новых технологических паспортов;-
с учетом новых технологических паспортов определяют второй вариант предельно допустимой программы НПД и соответствующую прибыль;-
повторяют несколько раз процедуры определения (уточнения) масштабов затрат на развитие, их распределения по направлениям, следующего варианта предельно допустимой программы НПД и ожидаемой прибыли.При сходимости процесса уточнения в пределе должны определиться согласованные программы НПД и развития предприятия, обеспечивающие получение максимальной прибыли при полном использовании мощностей.
3)
Возможна процедура формирования программы развития независимо от заданной или предельно допустимой программы НПД. При этом в качестве цели выбирается не максимальная прибыль, а развитие мощностей структурных единиц, обеспечивающее при заданных затратах минимальное отклонение текущих мощностей от предельных или требуемых, которые определяются на основе усредненного портфеля заказов с учетом нормативных моделей работ.При реализации схем циклически определяются по исходным данным варианты производственно-финансового плана, а исходя из его технико-экономических показателей
- соответствующие масштабы затрат на развитие и распределение их по направлениям, затем оценивается динамика изменений ожидаемой прибыли и уточняются исходные данные.Общими исходными данными для обеих схем являются:
-
частные и интегральные показатели НПД, гипотезы о зависимости частных показателей от затрат на их улучшение [38];-
технологические паспорта структурных единиц, включающие их производственные мощности по видам работ и нормативные модели основных процессов (разработка изделий, техническая подготовка производства, серийный выпуск и техническое обслуживание).И, наконец, укажем инструментальные средства реализации схем:
-
алгоритм многотемного планирования (МТП), использующий нормативные модели основных процессов;-
алгоритм определения оптимальной нормы прибыли Q, направляемой на развитие (ОНП), который использует магистральное решение соответствующей задачи;- алгоритм оптимального распределения ресурсов (ОРР) по направлениям развития, который реализует итерационный метод решения линеаризованных условий параметрической оптимизации.
В заключение раздела приведем пример постановки и метода решения задачи оптимального распределения ресурсов. Напомним, что задачи распределения ресурсов возникают при формировании и обосновании программы технического перевооружения предприятия или отрасли, при разработке концепции социально-экономического развития региона и т.д. Определяющими в этих случаях являются способ оценки близости набора показателей, характеризующих проект, к требуемым и вид зависимости значений этих показателей от предполагаемых затрат на их улучшение, т.е. выделяемых ресурсов.
Для предприятия частными показателями являются уровень автоматизации, производительность труда или трудоемкость работ (по проектированию и испытаниям новой техники, по технической подготовке и серийному выпуску продукции, по техническому обслуживанию), а интегральными – суммарная мощность структурных единиц предприятия или степень соответствия мощностей программе НПД.
Формулировка задачи определяется принимаемой гипотезой о виде зависимости между затратами
v на улучшение показателя x(v) характеризующего направление развития в начале и конце рассматриваемого периода. Можно считать [ 11] , что: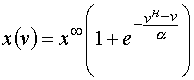 (1)
(1)
или
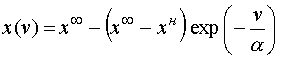
где
vн- начальные затраты;x
н, x? - соответственно начальное и предельное значение показателя;?
– коэффициент нормирования затрат, т.е. эффект на единицу затрат.Значения указанных параметров определяются методами регрессионного анализа по ряду прототипов или на основе экспертных оценок. Физический смысл формулы (1) легко объяснить, определив по ней отношение
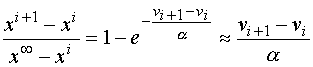 (2)
(2)
где:
xi – значение частного показателя на i-ом шаге развития.Отсюда следует, что. улучшение частного показателя одного из устройств (направлений) на (
Степень соответствия мощностей предприятия заданной программе НПД (или бизнес-плану основной деятельности) можно оценить суммой квадратов их отклонений от требуемых для ее реализации по видам работ (или от предельных).
Итак, предлагается итеративная схема решения задачи в общем случае, основанная на линеаризации условий оптимальности, с теоретическим и экспериментальным обоснованием сходимости получаемых приближений [
21] .Для математической формулировки задачи исходными являются:
Мощность по направлению
![]()
где в соответствии с принятой гипотезой (1) затраты на повышение производительности труда
v и рост численности (и профессиональной подготовки) персонала w определяются формулами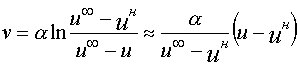
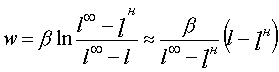 .
.
При фиксированной численности
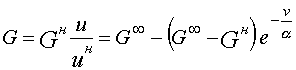
по аналогии с формулой (1).
При неопределенности программы НПД задача оптимального распределения ресурсов сводится:
- к минимизации суммы относительных отклонений частных показателей от предельных
![]() > min (4)
> min (4)
где
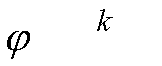
в соответствии с формулой (1);
- к оптимизации суммы мощностей
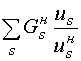 > max, (5)
> max, (5)
или
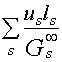 > max , (6)
> max , (6)
с учетом формулы (3).
Если известен состав выполняемых работ, т.е. программа НПД, определяются требуемые производительности труда
- к минимизации суммы квадратов относительных отклонений
us от требуемых![]() > min, (7)
> min, (7)
где
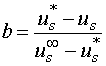 ;
;
- к минимизации суммы квадратов отклонений
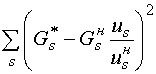 > min (8)
> min (8)
или
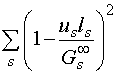 > min (9)
> min (9)
с учетом формул (3);
- к минимизации суммарных затрат на создание заданных мощностей по видам работ с учетом формул (3)
![]() > min (10)
> min (10)
при
Все задачи (4) – (10) должны решаться с учетом ограничений на суммарные затраты
Любая задача о распределении ресурсов, обеспечивающем оптимизацию функции стоимости
F(x) при заданном значении другой функции ограничений Ф(х) = Q, сводится к решению уравнений Куна-Таккера![]() ,
(11)
,
(11)
где
при Ф(х) =
Q.При этом функция стоимости
F(x) представляет зависимость основных требований к варианту технического развития от характеристик средств для его реализации типа формул (4) – (9), функция ограничений Ф(х) представляет зависимость суммарных затрат от характеристик средств для реализации выбранного варианта развития типа формулы (3). При отсутствии аналитического решения задачи (11) ее приближенное решение находят численными методами.В работе [
21] рассмотрен общий подход к итеративному построению такого решения. Предлагается уравнения (11) линеаризовать в окрестности нулевого приближения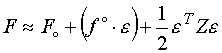 ,
, ![]() ,
,
где
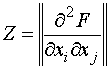 , ? = x
- xi
, ? = x
- xi
Тогда уравнения
(11) приобретают вид![]()
![]()
Их решение дается формулами, на основе которых строится итерационная процедура уточнения
![]() ,
, ![]()
где
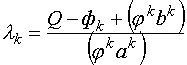 (12)
(12)
Методом индукции можно показать, что при замене
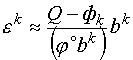
поэтому можно в общем случае принять вместо
(12)![]() , (13)
, (13)
где
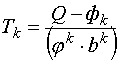 в соответствии с
условием
в соответствии с
условием 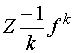 ,
определяемому дифференциальными свойствами
функции стоимости F(x).
,
определяемому дифференциальными свойствами
функции стоимости F(x).
Так как отклонение Ф от заданного значения после уточнения
xk будет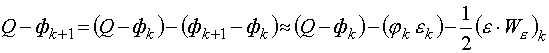
где
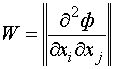 ,
,
то из
( 13) следует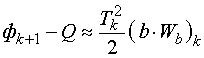 .
.
Обозначая
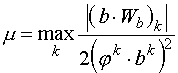 , имеем
, имеем При
В результате нахождения формального решения задачи распределение ресурсов (аналитическими методами или по предложенной методике уточнения начального приближения) может оказаться, что для некоторых направлений
В силу необратимости затрат следует исключить из рассмотрения соответствующие частные показатели и заново решить задачу для остальных. Аналогично следует поступать, если некоторые значения
Дополнительно укажем здесь, что авторами разработан метод “именных множителей Лагранжа”, позволяющий автоматически учитывать необратимость затрат и дискретность переменных.
В работе [18] на базе такого рода расчетно-оптимизационного подхода и обобщения других известных подходов были формализованы следующие процедуры:
-
прогнозирование показателей деятельности с оценкой жизненного цикла их изменения и масштабов затрат на их улучшение;-
формирование программ основной деятельности и развития крупного промышленного объединения;-
совершенствование организационной структуры, механизмов управления крупного промышленного объединения и средств поддержки управленческих решений с использованием принципа адаптационной оптимизации.Дополнительно отметим, что на базе специально созданных моделей и экспертных оценок на примере [18] можно решать задачи:
1)
выбора типа и состава технических средств для развития материальной базы, обеспечивающих выполнение необходимых требований при минимальных затратах;2)
автоматического формирования плановых документов, обеспечивающего многотемное планирование с максимальной загрузкой структурных единиц или с минимальным нарушением договорных обязательств;3)
обоснования программы развития предприятия на определенный период с оптимальным распределением ограниченных ресурсов по нескольким направлениям.По нашему опыту такие модели и методы могут быть использованы:
Величину ресурсов
Q, выделяемых из общей (ожидаемой) прибыли на улучшение показателей Gj по направлениям развития, можно определить на основе магистрального решения задачи выбора оптимальной нормы капитальных вложений с использованием модели накопления и роста. Величины требуемых значений Gj* определяются для заданного тематического плана на основе алгоритма многотемного планирования с использованием нормативных моделей работ.При децентрализации управления и развития горизонтальных связей указанный подход становится актуальным для отдельных предприятий, входящих в состав крупных объединений.
2.3. Имитационное моделирование
Метод имитационного моделирования возник в 60-х годах прошлого века как метод исследования, заключающийся в имитации на компьютере процесса функционирования первоначально схем и структур цифровых устройств, а потом и вообще любого оборудования, для описания процесса работы которого можно было составить алгоритм.
Задачей имитационного моделирования является всестороннее определение правильности функционирования устройств, их характеристик и других качеств чаще всего еще до физического изготовления исследуемых устройств.
Как указано в [1] в самом общем виде структуру имитационной модели можно представить математически в виде
E = f(xi, yi),
где:
E – результат действия системы;xi
– переменные и параметры, которыми можно управлять;yi
– переменные и параметры, которыми управлять нельзя.Сказанное подчеркивает зависимость функционирования такого рода систем как от контролируемых, так и от неконтролируемых переменных. Каждая модель представляет некоторую комбинацию таких составляющих, как
Сущностью метода имитационного моделирования является разработка программного алгоритма процесса функционирования некоторой структуры или схемы с учетом выбранного уровня детализации и проведения исследований для получения нужных внутренних характеристик и оценок влияния возможных отклонений. В принципе, этот метод позволяет исследовать структуры и схемы любой степени сложности и детализации.
Проблематикой основных направлений развития и использования метода имитационного моделирования являются:
К первому направлению относят задачи разработки моделей потоков входных сообщений и типовых моделей, задачи использования математических моделей в качестве элементов имитационных моделей, задачи преобразования имитационных моделей с целью упрощения программ и увеличения их быстродействия.
Второе направление составляют задачи использования и обработки статистического материала, задачи исследования соответствия имитационной модели реальному объекту на основе накопленного статистического материала.
Третье направление составляют задачи разработки систем автоматизации программирования, ориентированных на задачи моделирования Специфика задач моделирования на различных этапах проектирования позволяет выделить, по крайней мере, два подкласса таких систем.
Во-первых, это системы, обладающие развитыми общеалгоритмическими средствами, имеющие широкий набор средств описания параллельно выполняемых действий, описания временных диаграмм выполнения процессов, а также развитые средства сбора и обработки статистического материала.
Во-вторых, это системы, позволяющие в удобной и сжатой форме отразить логические и топологические особенности моделируемых объектов, обладающие средствами преобразования форматов, средствами записи микропрограмм и т.п.
В соответствии с [1] имитационное моделирование определяется как экспериментирование с моделью реальной системы. Необходимость решения задачи путем экспериментирования становится очевидной, когда возникает потребность получить о системе специфическую информацию исследовательского характера.
Там же подчеркивается, что непосредственное экспериментирование на реальной системе устраняет много затруднений, если необходимо обеспечить соответствие между моделью и реальными условиями, однако недостатки такого экспериментирования весьма значительны, поскольку:
По этим причинам исследователь должен рассмотреть целесообразность применения имитационного моделирования при наличии любого из следующих условий:
Разработка и использование имитационной модели позволяет экспериментатору видеть и “разыгрывать” на модели реальные процессы и ситуации. Это в свою очередь должно в значительной мере помочь ему понять и прочувствовать проблему, что стимулирует процесс поиска нововведений. Мы далеки здесь от утверждения, что решения на моделях являются для реального управленца критерием истины. Скорее это подтверждение стимулирующей роли такого рода моделирования для принятия управляющих решения зачастую весьма далеких от модельных рекомендаций. Достаточно полный обзор работ по имитационному моделированию содержится, например, в [40].
2.4. Алгоритмическое моделирование и другие подходы
к описанию и анализу задач планирования
Понятие алгоритмического моделирования возникло в середине 70-х годов прошлого века, когда терминология моделирования стала активно использовать понятие информации. Без особого ее определения в литературе стали приводиться утверждения следующего плана, например, публикация, которую можно считать достаточно типичной для изложения алгоритмического моделирования: “После того как сформулирована цель исследования, наступает этап ознакомления с информацией, относящейся к предмету исследования. Далее следует этап формирования рабочей гипотезы и присущей ей модели исследуемого явления. Следующий этап – работа с моделью, что, как правило, включает в себя сложную обработку информации, особенно когда используется математическая или алгоритмическая модель” [22].
Интересно, что после этого следует признание, что на начальной стадии исследования задача может быть формализована только на естественном или профессиональном языке конкретной специальности (
Интересно, как бы это сделать (формализовать!) на уровне естественного или профессионального языка? Да только отказом от них – поиском чего-то другого. Только управлять от этого легче не становится, попробуйте-ка управлять не на своем родном, профессиональном, управленческом!). Предлагается перевести гипотезу, сформулированную на естественном языке, на язык математики, после чего построить алгоритм, что также является неформальной операцией (Это, говоря на современном языке, знаковое признание. Сколько лет потребовалось, чтобы до конца понять – нет, и не может быть ни одного оптимизационного алгоритма, впрямую вытекающего из математических построений. Всегда придется учитывать “проблемные особенности”, реалии ситуации, которые уже не ложатся на язык математики, но еще в некоторой степени описываются языком алгоритма, который в этом смысле оказывается выразительнее языка математики.).Вот из-за этой неформальности и предлагается введение и использование алгоритмических моделей (восприятие алгоритмов как моделей), представляющих собой “комплекс данных и программ, позволяющий получить с помощью вычислительной техники результаты, необходимые для подтверждения принятой гипотезы”.
Достаточно ясно, что на этом все не кончается. Процедура формализации естественного языка так и остается нерешенной проблемой. В литературе признается, что если фактически ограничиться только набором числовых параметров после формализации постановки, то можно ограничиться их рассмотрением в линейном метрическом пространстве. Если же необходимо присутствуют нечисловые элементы, то с ними можно работать, если они образуют вполне упорядоченные множества. При одновременном использовании числовых и нечисловых элементов подход использован быть не может.
Итак, для решения задач управления, как задач оптимизационных, данный вариант моделирования существенной ценности не представляет. Кроме того, специалистам достаточно ясно, что алгоритмическое моделирование в такой постановке, как оно публиковалось в литературе, является не более чем ограниченным вариантом имитационного моделирования, которое мы уже рассмотрели выше.
Можно перечислить еще много различных вариантов моделирования и отдельных задач, в частности, см. [39,40], где среди прочих методов рассматриваются авторские разработки технологии моделирования на основе формализации алгоритмических сетей, но для практика вполне достаточно, если мы ограничимся здесь таблицей употребляемости традиционных подходов, наиболее часто используемых при внутрифирменном планировании, из [1].
Таблица
2.1Подходы и методы |
Частота использования |
Процент |
Имитационное моделирование |
60 |
29 |
Линейное программирование |
43 |
21 |
Сетевые методы |
28 |
14 |
Теория управления запасами |
24 |
12 |
Нелинейное программирование |
16 |
8 |
Динамическое программирование |
8 |
4 |
Целочисленное программирование |
7 |
3 |
Теория массового обслуживания |
7 |
3 |
Прочие |
12 |
6 |
Всего |
205 |
100 |
Все, указанное в этой таблице, легко найти в распространенных учебниках, поэтому ниже можно сразу перейти к рассмотрению общих вопросов теории моделирования, без чего наш анализ будет неполным.
2.5. От теории моделей к повествовательно-прецедентному
изложению подходов к организационному управлению
Если рассматривать общие направления модельного подхода, оценивать его перспективы для обеспечения адекватного представления (описания) реальных природных объектов, то исходить следует из анализа просматриваемых путей развития наиболее общего направления моделирования – теории моделей.
Теория моделей – раздел математики, пограничный между математической логикой и алгеброй [23]. В ней считается, что всякая теория
T класса объектов К связана с называемым сигнатурой набором ? понятий, отношений и операций, которые являются основными в теории, а сама эта теория Т является множеством высказываний языка L сигнатуры ?, истинных на каждом объекте из К.Такой подход вполне сравним с аналогичным в общей теории систем (ОТС). Согласно М.Месаровичу ОТС должна быть настолько общей, чтобы могла охватить многие уже существующие теории, касающиеся в том или ином разрезе теории систем. Как частные случаи из ОТС должны выводиться, например, теория динамических систем, теория конечных автоматов, теория алгоритмов и т.д. При этом научные основания ОТС должны быть настолько фундаментальны, чтобы ее выводы имели практическую ценность при изучении конкретных систем, встречающихся в жизни.
Термин “общая” здесь означает, что ОТС имеет дедуктивный характер и объединяет другие теории - те, которые изучают системы в целом и те, которые рассматривают поведение систем (теорию управления, адаптации, самоорганизации и т.п.). Используемые в ОТС уровни абстрактного описания систем используются как разъяснение термина “система”. Для этого предлагается использование наиболее абстрактных областей математики: теории множеств, общей топологии, абстрактной алгебры и т.д. Термин “теория” по М.Месаровичу определяется в духе работ по математической логике и основаниям математики, в которых для его введения предварительно дается понятие о классе элементарных высказываний Р. Тогда “теория” определяется как подкласс
Вне всякого сомнения, такого рода постановки исследований имеют не только право, но и обязанность существования, как одна из опор математизации научных исследований и, в частности, оптимизации для организационного управления. Но их связь с реальной практикой управления в условиях постоянных непрогнозируемых воздействий и решений, имеющих силу на порядки выше всех граничных и начальных условий, явно недостаточна и, самое главное, в перспективе установление таких связей не просматривается.
Поэтому далее мы рассматриваем изложение материала в ключе книг [24,25,26], которые уже давно от математического подхода перешли к повествовательно-прецедентному изложению проблем управления. Ничего в этих книгах не упрощено относительно классического математического подхода. Просто сделана честная попытка, не затрагивая и не критикуя его основы, опереться на разум и опыт профессионалов, долженствующих в силу своих обязанностей управлять, не смотря ни на что, и управлять разумно.
Частично их подход опирается на подход к формированию ОТС по фон Берталанфи. Согласно работам фон Берталанфи ОТС представляется как теория описания систем вообще, где на первом месте стоит иерархическая классификация систем и далее, каждый уровень иерархии анализируется с использованием того аппарата, той степени абстракции, которые допустимы на данном уровне системной сложности для достижения конкретной цели текущего исследования (управления).
По фон Берталанфи в научном анализе систем выделяют три этапа. Согласно этой градации, на первом этапе в науке рассматривается “организованная простота” (механика), на втором – “беспорядочная сложность” (статистическая физика), на третьем – “организованная сложность” (ОТС). Для связи с нашим текущим изложением материала достаточно напомнить, что такой подход базируется на понятии “собственного отношения объекта к информации”. Пожалуй, единственное, что мешает восприятию этого подхода для реализации нужд реального управления, это не сформулированное в теории фон Берталанфи отношение к информации как к феномену, явлению как таковому, хотя, возможно, и не субстанциональному о чем мы будем говорить во второй части.
А пока нам надо рассмотреть известные на сегодняшний день принципы организации “не математического” управления фирмами на том языке и в том стиле изложения, который используется в современных учебных и научных изданиях по проблемам управления и менеджмента, для выявления реальных возможностей такого управления, и далее сформировать подход, по возможности исключающий выявленные недостатки.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|