 |
||
4. О самоподобии Золотой Пропорции.
В последнее время термин “Золотая Пропорция” прочно ассоциируется с такими математическими понятиями, как “фрактал”, “хаос”, “самоподобие”. Что же имеется в виду? Попробуем записать Золотую Пропорцию в виде непрерывной дроби:
![]()
t = a0 +
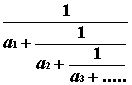
Используем для этого формулу t
= 1 + t -1 :t = 1 + 1 / ( 1 + t -1 ) = 1 + 1 / ( 1 + 1 / ( 1 + t -1 ) ) = ….. ,
то есть:
t = 1 +
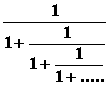
Получилась “вложенная” бесконечная дробь, каждое из “вложений” которого равно (“подобно”) всей дроби в целом.
За это свойство Золотую Пропорцию иногда называют “самым иррациональным числом”.
Поскольку мы обратились к выражению t
= 1 + t -1 , выведем из него несколько формул.Разложим функцию
f(x) = 1 / ( 1 + x ) в ряд Тейлора в точке x = 0 :f(x) = f(0) + f’(0)*(x-0) / 1! + f’’(0)*(x-0)2 / 2! + …..
Получился ряд:
f(x) = ∑ (-1)n x n , n = 0, 1, 2, …….Подставим
x = t -1 :f(t -1) = 1 – 1/t + 1/t 2 – 1/t 3 + …..
С другой стороны:
f(t -1) = 1 / (1 + 1/t ) = 1/tПолучилось следующее разложение для t
-1 :t -1 = ∑ (-1)n t -n = 1 – 1/t + 1/t 2 – 1/t 3 + ….. , n = 0, 1, 2, ……. (1)
Сложим соседние члены ряда :
1/t 2n – 1/t 2n+1 = 1/t 2(n+1)
То есть : t
-1 = ∑ t -2n = 1/t 2 + 1/t 4 + ….. , n = 1, 2, ……. (2)( Аналогичным способом, складывая
1/t 2n-1 и -1/t 2n , получим :t -1 = 1 - 1/t 3 - 1/t 5 - ….. , n = 1, 2, ……. (3) )
Из формулы
(2) следует : t = 1 – 1/t = 1 + 1/t 2 + 1/t 4 + ….. ,то есть само З.С. в троичном представлении имеет следующую запись:
t = 1,(1) = 1,1111111 …..
Приведем в заключение еще одно самоподобное выражение для З.П. (без док-ва):
t = ![]()
далее
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|