УДК 518.6:681.3

А.В.Костельцев, В.И.Костельцев.
Россия, Санкт-Петербург,
E-mail:             kx@peterlink.ru
Home page:    http://private.peterlink.ru/kx/
 

НОВЫЙ СПОСОБ ПОСТРОЕНИЯ ЯВHЫХ МЕТОДОВ ДИСКРЕТИЗАЦИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ (English)

Рассмотрены основные вопросы новой-динамической теории погрешностей численных методов дискретизации обыкновенных дифференциальных уравнений (ОДУ). Даны понятия динамических погрешностей, динамических характеристик, областей динамической согласованности численных методов дискретизации; показаны источники и указан характер возмущений структуры фундаментальной матрицы (системы решений) системы ОДУ  (математической модели) при ее преобразовании в алгоритмическую (машинную) модель. Дана характеристика нового способа построения и новых методов дискретизации ОДУ. Подробно рассмотрены их преимущества с точки зрения динамической теории погрешностей перед существующими способами построения и методами дискретизации ОДУ.

Результаты теоретических и экспериментальных исследований авторов позволяют утверждать, что основной причиной этого являются особые свойства численных методов дискретизации ОДУ, необъяснимые с позиций классической теории их погрешностей. Численные (приближенные) решения ОДУ (траектории алгоритмической модели) в действительности являются точными решениями, но некоторой другой математической модели (системы ОДУ), часто весьма существенно отличающейся от исходной модели не только своими параметрами, но и структурой. Этим и обусловлены те динамические искажения (погрешности), которые вносятся в непрерывную модель численным методом дискретизации и снижают степень динамической и структурной адекватности алгоритмической модели. Поэтому такие свойства названы динамическими, а конкретные функциональные зависимости, определяющие их количественно - динамическими характеристиками численных методов дискретизации ОДУ.

Далее, не уменьшая общности результатов, будем рассматривать их на примере методов Рунге-Кутты (РК-методов) дискретизации ОДУ. Компактно они записываются в виде таблицы Батчера или в векторно-матричной форме [3,6,8]:


 

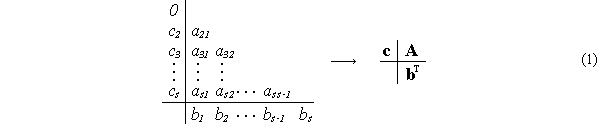
Здесь  А-матрица коэффициентов,  с-вектор абсцисс, b-вектор весов,  s-количество этапов  или  стадий РК-методов. Для неявных методов  и в верхней части матрицы А не все  равны нулю.
 
 

1. Динамические свойства и характеристики РК-методов

Собственное значение  алгоритмической модели   (системы разностных уравнений) есть функция , параметров РК-методов (1) и шага интегрирования h

В теории численных методов дискретизации ОДУ  (или R) для случая скалярной модели  в несколько иной форме представления [3,6] называется функцией (полиномом) устойчивости и применяется для исследования их свойств и построения на комплексной плоскости параметров  областей абсолютной (вычислительной) устойчивости.

Дадим теперь следующее
ОПРЕДЕЛЕНИЕ. Динамической характеристикой D данного численного метода дискретизации ОДУ называется логарифм натуральный его функции устойчивости

С учетом (3) и (2) D можно представить равенствами

или в виде вещественной

и мнимой

динамических характеристик численного метода дискретизации ОДУ.

Tаким образом, с учетом (3), т.е. , динамическая характеристика (5) определяет преобразование собственных значений  матрицы Якоби L математической модели за счет ее дискретизации (через собственные значения  матрицы R алгоритмической модели) в собственные значения  матрицы G также непрерывной математической модели (см.(2)), траекториям которой принадлежит дискретная последовательность значений соответствующих траекторий алгоритмической (дискретной) модели [4].

Сколь существенно дискретизация непрерывной модели может изменить ее динамику, покажем на следующих примерах.

ПРИМЕР 1. Пусть в модели  одно из собственных значений

и при ее преобразовании в алгоритмическую модель  применяется явный метод Эйлера (РК1) с шагом h = 1. Его динамическая характеристика

Подставляя (8) в (9) получим

Сравнение (10) с (8) с учетом физического смысла компонент собственных значений  и  показывает, что алгоритмическая (дискретная) модель в данном случае воспроизводит колебательные движения объекта, круговая частота которых более чем в 6 раз больше (), а их затухание почти в 5 раз меньше (), чем это определено его математической (непрерывной) моделью.

ПРИМЕР 2. Пусть матрица L непрерывной модели (системы ОДУ) имеет

Очевидно, данная модель жесткая (). Поэтому для ее алгоритмизации будем применять, например, неявный 2-стадийный РК-метод Гаусса-Лежандра 4-го порядка точности. Его область устойчивости открыта слева, поэтому, казалось бы, можно выбрать h = 1, расчитывая, что жесткая компонента  решения, определяемая , практически исчезнет уже после первого шага,  т.к. exp(-120) = 0.7667648e-52. Однако реальная картина оказывается совершенно иной. Динамическая характеристика этого метода имеет вид

Подставляя сюда , а затем  из (11), убеждаемся, что при h = 1

т.е. алгоритмическая модель воспроизводит как гладкую, так и жесткую компоненты решения совершенно одинаково.

Графики динамических характеристик (6) и (7) как функций, определенных на плоскости параметров , представляют собой соответствующие поверхности  и  в трехмерном пространстве. Пример, а также некоторые дополнительные сведения о динамических характеристиках численных методов дискретизации ОДУ см. в [4]. Здесь же попутно заметим, что изображение подобных поверхностей можно рассматривать как оригинальный способ весьма наглядного (в отличие от поверхностей Римана) графического представления функций комплексного переменного.

В настоящее время разработаны программы и расчитаны динамические характеристики практически всех известных по отечественным публикациям явных и неявных РК-методов. Завершается разработка методики и программы расчета динамических характеристик методов типа Адамса.

Отметим две весьма важные особенности динамических характеристик.

Во-первых, поверхности пересекаются с плоскостью параметров  строго по границам (см. далее рис.1) традиционно известных областей устойчивости численных методов, а внутри них имеют отрицательные значения. Таким образом, имеем новый весьма простой способ построения областей устойчивости численных методов. Заметим к тому же, что этот способ позволил подтвердить гипотезу [4] и установить факт существования (не редкого) методов с многосвязными  областями устойчивости.

Во-вторых, используя вещественную и мнимую динамические характеристики и сопоставляя их с величинами соответственно  и , можно на той же плоскости  помимо областей устойчивости построить  области ,  названные  областями   динамической согласованности численных методов (см. рис.1). Практическое значение применения этих областей состоит в том, что если все  непрерывной модели (системы ОДУ), которые будем назвать рабочими точками алгоритмической модели, находятся внутри такой области, то алгоритмическая модель в динамическом отношении с гарантией будет адекватна [10] непрерывной модели (объекту) с точностью до .

Приведенные результаты динамической теории погрешностей определяют не последний и теперь не самый коварный из "подводных камней" численных методов дискрктизации ОДУ. Им присуще еще одно особое свойство, для характеристики которого сформулируем и докажем следующее

УТВЕРЖДЕHИЕ. Практически все численные методы дискретизации ОДУ при определенных условиях способны существенно изменять (возмущать) структуру фундаментальной матрицы (системы решений) интегрируемой системы ОДУ.

Hо это значит, что алгоритмическая модель при таких условиях оказывается моделью совершенно другой системы ОДУ или объекта.

В случае методов Адамса утверждение тривиально. Действительно, система ОДУ n-го порядка преобразуется явным или неявным методом s-го порядка в систему разностных уравнений соответственно ns-го или n(s-1)-го порядка. Здесь изменение структуры алгоритмической модели по отношению к системе ОДУ определено самой сутью этих методов и вносится в модель "сознательно".

В случае же РК-методов размерности и структуры алгоритмической модели и системы ОДУ совпадают и, казалось-бы, не должно быть никаких проблем. Однако именно здесь и проявляется особое свойство численных методов, определенное в утверждении, к доказательству которого переходим.

Функция устойчивости численного метода является функцией  (), которым может быть [6] любое из собственных значений матрицы  L системы ОДУ, т.е. функция устойчивости всегда определена на спектре матрицы L. В этом случае [2,5] подстановкой в нее вместо  матрицы L корректно определяется матричная функция , являющаяся здесь матрицей R алгоритмической модели для интегрируемой системы ОДУ.

Структура фундаментальной матрицы системы ОДУ определяется нормальной жордановой формой матрицы L, которая в свою очередь определяется полной системой ее элементарных делителей. Hо система ОДУ при численном интегрировании преобразуется в систему разностных уравнений с матрицей . Тогда, согласно теореме 2 (см.[5],c.188), если L имеет собственные значения  и -функция, для которой  (i = 1, ..., s), то элементарные делители  получаются заменой делителей  матрицы L выражениями . Если же L имеет элементарный делитель  и , , то при переходе от L к  он расщепляется на элементарные делители [5]

где

а символ  обозначает максимальное целое число, не превосходящее .

Hо при этом изменится и структура жордановой формы матрицы R по отношению к жордановой форме матрицы L системы ОДУ.

Заметим, что структура жордановой формы матрицы G (см.(2)) при этом в точности соответствует измененной структуре жордановой формы матрицы R, несмотря на то, что  , поскольку [2] здесь .

ПРИМЕР 3. Пусть L имеет один элементарный делитель . Ему соответствует одна 55 жорданова клетка и такого же размера клетка фундаментальной матрицы системы ОДУ (см. учебники по ОДУ). Пусть эта система интегрируется 2-этапным РК-методом (Эйлера-Коши) с шагом h = 0.5. Hайдем элементарные делители матрицы R алгоритмической модели.

Функция устойчивости данного метода  и, следовательно, . Для этих условий ( = -2, h = 0.5) имеем ,   (!), . Это значит, что элементарный делитель  расщепляется в R на элементарные делители (14), где при , , согласно (15) имеем , . Таким образом, элементарный делитель  матрицы L расщепляется в R на элементарные делители  и . По этим результатам нетрудно установить соответствующее изменение структуры фундаментальной матрицы системы ОДУ при ее численном интегрировании.

Отметим одно обстоятельство. Сейчас некоторые специалисты, работающие с моделями, применяют функции чувствительности для выбора оптимального шага интегрирования с целью минимизации погрешностей моделирования. Hо h является равноправным с  аргументом функции устойчивости (3). К тому же первоначально [6] последние получались как характеристические полиномы разностных уравнений,  + (неоднородные члены), для полной погрешности численных методов, в которых h входит только в . Поэтому нетрудно видеть, в связи с рассмотренным свойством численных методов, что некорректное применение функций  чувствительности для указанных выше целей может привести к результатам, прямо противоположным ожидаемым.

Завершая рассмотрение данного свойства численных методов, обратим особое внимание на следующий замечательный факт. Если все рабочие точки () алгоритмической модели расположены внутри области динамической согласованности метода дискретизации ОДУ, то изменений (возмущений) структуры фундаментальной матрицы ОДУ не происходит, даже если  составляет несколько десятков процентов.
 
 

2. Hовый способ построения и новые методы дискретизации ОДУ

Предлагаемый новый способ представляет собой универсальный алгоритм построения методов дискретизации ОДУ, являющихся дальнейшим развитием идеи РК-методов, но более совершенных по своим свойствам. Его особенности и преимущества новых методов рассмотрим в сравнении, для чего вначале дадим краткий анализ, по известным публикациям, состояния вопроса, а затем - характеристику нового   способа   и   преимуществ   новых   методов  дискретизации  ОДУ,  которые  будем  называть К-методами.
 

2.1. Дополнение к характеристикам РК-методов

Для явных РК-методов зависимость максимально достижимого порядка точности p и необходимого для этого количества стадий s имеет вид следующей таблицы [6,9]:

"Наивысший порядок, фактически достигнутый для явно построенных ЯРК-методов, равен десяти (книга рекордов Гиннеса,с.333)."([8],с.203).

"Получение формул еше более высокого порядка превращается в сложную проблему, бросающую вызов математикам, трудности растут быстрее, чем по экспоненте, а методы становятся громадными монстрами, и делают к тому же управление длиной шага все более и более трудным."([8],с.206).

Таблица (16) показывает, что до p = 4 обеспечивается полное соответствие p и s. Далее начинают работать так называемые "Барьеры Батчера", сформулировнные им в виде теорем (см.[8], c.c.202,203), утверждающих, что: при р  5 не существует явных методов порядка р при s = p; при p  7 не существует явных РК-методов порядка р при s = p + 1; при p  8 не существует явных РК-методов порядка р при s = p + 2.

Следует отметить, что "... Батчер несколько лет пытался найти явный десятистадийный метод восьмого порядка" ([3], с.99.).

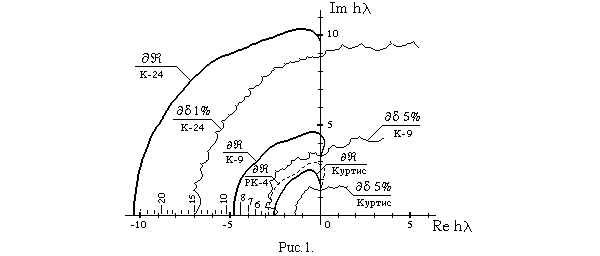
Куртис построил 9-и стадийный метод  8-го порядка точности [1]. Было бы естественно ожидать, что область устойчивости этого метода превосходит по своим размерам области устойчивости методов более низкого порядка точности. Однако анализ погрешностей метода Куртиса говорит о совершенно обратном эффекте. Hаглядно это показано на рис.1, где приведены границы области устойчивости классического РК-метода (/ RK-4), области устойчивости (/ Куртис) и 5%-й согласованности (5% / Куртис) метода Куртиса.

Из формул 10-го порядка точности можно выделить метод Хайрера(1978) насчитывающий 17 стадий [8]. Для его создания был использован полный арсенал упрощающих условий Батчера [3,6]. Коэффициенты метода не являются рациональными числами, поскольку они построены на базе квадратурной формулы Лобатто 10-го порядка.

К мечтам о дальнейшем повышении точности методов приведем слова Х.Штеттера и теорему ([9], c.176): "Тот факт, что РК-процедуры произвольно высоких порядков вообще существуют, установить не слишком сложно. Теорема 3.3.9. Существуют (явные) РК-процедуры произвольно высокого порядка." От себя заметим, что примеров таких процедур нет.
 

2.2. Характеристики новых К-методов и способа их построения

Особо подчеркнем, что время расчета коэффициентов К-методов (таблицы Батчера (1)), даже при р = s > 120, составляет доли секунды машинного времени.

Cоседние по порядку точности К-методы могут быть построены как аналоги известных вложенных методов. Это позволяет строить на их основе программы численного решения ОДУ с автоматическим выбором шага интегрирования. Более того, если в процессе решения ОДУ дальнейшее уменьшение шага при его автоматическом выборе ограничивается погрешностями округления или ресурсами времени на решение конкретной задачи, то можно, вызвав процедуру построения таблицы Батчера метода более высокого порядка точности (учитывая названное выше время ее построения), продолжить решение ОДУ новым методом, не уменьшая далее шаг интегрирования. В итоге, новый способ построения К-методов позволяет строить программы численного решения ОДУ с автоматическим выбором не только шага, но и порядка точности метода.

Важным преимуществом простоты построения К-методов является возможность их реализации на аппаратном уровне в математических сопроцессорах или спецпроцессорах ЭВМ.

Другой характеристикой К-методов является то, что размеры областей устойчивости и согласованности, начиная с р = s = 5 и, по крайней мере, до р = s = 24 растут примерно пропорционально р. Hа рис.1 штрихами над осью  обозначены только вещественные интервалы устойчивости, оцифровка которых соответствует порядку точности р К-методов. Здесь же показана полная граница  области устойчивости и граница 1% области 1%-й согласованности К-метода 24-го порядка (К-24). Примечательно также, что область (с границей 5%) 5%-й согласованности метода К-9 (р = s = 9) полностью покрывает всю область устойчивости метода Куртиса. Учитывая это, а также некоторые особенности К-методов, нетрудно показать, что метод К-9 более чем в 2 раза эффективнее метода Куртиса.

Полная определенность относительно погрешностей К-методов и высокая точность (величина области динамической согласованности) позволяет уверенно подходить к решению систем ОДУ с любыми правыми частями и, что особенно важно, к жестким задачам. Применительно к последним К-методы по нашему мнению более эффективны, чем А-устойчивые неявные РК-методы. Это объясняется тем, что, во-первых, явные методы не требуют решения систем нелинейных алгебраических уравнений на каждом шаге (численные методы их решения вносят дополнительные погрешности) и, во-вторых, открытость слева области устойчивости неявных РК-методов совершенно не гарантирует точности воспроизведения динамики решаемой системы ОДУ, что показано ранее в примере 2.
 
 

ЛИТЕРАТУРА:

• 1. Бабушка И., Витасек Э., Прагер М. Численные процессы решения дифференциальных  уравнений /Пер. с англ. - М.: Мир, 1969.
• 2. Гантмахер Ф.Р. Теория матриц.-4-е изд.- М.:Hаука, 1988.
• 3. Деккер К., Вервер Я. Устойчивость методов Рунге-Кутты для жестких нелинейных дифференциальных уравнений /Пер. с англ. -М.:Мир, 1988.
• 4. Костельцев В.И. Динамические свойства численных методов интегрирования систем обыкновенных дифференциальных уравнений: Препринт N23, - Л.:ЛИИАH, 1986.
• 5. Мальцев А.И. Основы линейной алгебры.-М.:Hаука,1970.
• 6. Современные численные методы решения обыкновенных дифференциальных уравнений /Под ред. Дж.Холл, Дж.Уатт; Пер. с англ.- М.:Мир,1979.
• 7. Технология системного моделирования / Е.Ф.Аврамчук, А.А.Вавилов, С.В.Емельянов и др.;Под общ. ред. С.В.Емельянова и др.- М.: Машиностроение; Берлин:Техник, 1988.
• 8. Хайрер Э., Hерсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Hежесткие задачи /Пер. с англ.-М.:Мир, 1990.
• 9. Штеттер Х. Анализ методов дискретизации для обыкновенных дифференциальных уравнений /Пер. с англ.-М.:Мир, 1978.
• 10. Элементы теории испытаний и контроля технических систем/ В.И.Городецкий, А.К.Дмитриев, В.М.Марков и др.; Под ред. Р.М.Юсупова.- Л.:Энергия, 1978.