 |
||
|
||
UDC 518.6:681.3.
Kosteltsev A.V., Kosteltsev
V.I.
Russia, St.Petersburg,
E-mail:
kx@peterlink.ru
Home page: http://private.peterlink.ru/kx/
correlation
of numerical methods of discretization are given; sources are shown and
character of disturbance of structure of fundamental matrix (system of
solutions) of ODE system (mathematical model) at its transformation to
algorithmic (computer) model. Characteristic of the new way of constructing
and new methods of ODE discretization are given. Its advantages from existing
ways of constructing and methods of ODE discretization are considered in
details from the point of view of dynamic theory of errors.Results of theoretical and experimental researches, performed by the authors, permit to assert that the main reason for that the specific properties of numerical methods of discretization of ODE are, that are non-explainable from positions of classic theory of their errors. Numerical (approximate) solutions of ODE (trajectories of algorithmic model) are actually exact solutions, but of some other mathematical model (ODE system), that often differs essentially from the initial model not only by its parameters, but by the structure as well. This fact effects in the dynamic distortions (errors) that are introduced to continious model by numerical method of discretization and that decrease the degree of dynamic and and structural adequacy of algorithmic model. Therefore these properties are called dynamic, and particular functional dependencies, defining them quanitatively - dynamic characteristics of numerical methods of ODE discretization.
Futher, without reducing generality
of results, we shall consider them on example of Runge-Kutta methods (RK-methods)
of ODE discretization. They may be compactly recorded in form of
Butcher table or in vector-matrix form [3,
6, 8]:
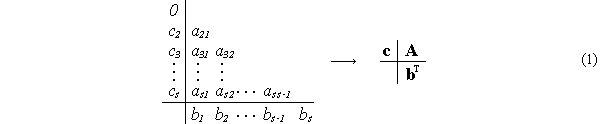
Here: A-matrix of coefficients,
c-vector of abscisses, b-vector of weights, s - number
of steps or stages of RK-methods. For implicit methods 
and in the upper part of matrix A not all 
are equal to 0.
Own value 
of algorithmic model 
(of the system of difference equations) is function 
of parameters RK-methods (1) and integration step h
In the theory of numerical methods of ODE discretization
(or R) for the case of scalar model 
in some other form of representation [3, 6]
is called function (polinom) of stability and is used to study their properties
and construction on complex plane of parameters 
of areas of absolute (computational) stability.
Now we give the following
DEFINITION.
The dynamic characteristic D of the given numerical method of ODE
discretization is defined as natural logarithm of its function of stability
Taking into consideration (3) and
(2) D may be represented by equations
or as real
and imaginative
dynamic characteristics of numerical
method of ODE discretization.
Thus, noting (3), i.e. 
,
dynamic characteristic (5) defines conversion of values 
of Jacobi matrix L of mathematical model due to its discretization
(via own values 
of matrix R of algorithmic model) to own values 
of matrix G of also continious mathematical model (see (2)), to
trajectories of which discrete sequence of values of corresponding trajectories
of algorithmic (discrete) model belongs[4].
Essence of influence of discretization
of continious model to its dynamics will be shown on examples.
EXAMPLE 1. Let in model 
be one of own values
and within its transformation to algorithmic model
explicit Euler method is used (RK1) with
step h =1. Its dynamic characteristic
Substituting (8) into (9) we obtain
Comparison of (10) with (8) in view of physical meaning of components
of own values
and 
shows that algorithmic (discrete) model in this case reproduces oscillatory
movements of object, circular frequency of which is more that 6 times greater
(
), and their
attenuation is almost 5 times less (
)
than it is determined ny its mathematical (continious) model.
EXAMPLE 2. Let matrix L of continious
model (ODE system) has
Obviously, this model is stiff (
).
Therefore for its algorithmization we shall use, for example, implicit
2-stage Gauss-Legandre RK-method of the 4th order of accuracy. Its area
of stability is left-open, thus, it seems to be possible to choose h
= 1, believing that stiff component of solution, determined by 
,
will practically disappear already after the 1st step, because exp(-120)
= 0.7667648e-52. However the real picture appears to be rather different.
Dynamic characteristic of this method is
substituting 
here, and then
from (11), we find that when h = 1
i.e. algorithmic model reproduces both smooth and stiff components
of solution completely equally.
Graphs of dynamic characteristics (6) and (7) as functions, defined
on plane of parameters ,
reproduce corresponding planes 
and 
in 3-dimensional space. For example, and some auxillary information about
dynamic characteristics of numerical methods of ODE discretization see
[4]. Here we shall notice, by the way, that
reproduction of the like surfaces may be considered as an original way
of rather evident (in difference from Riman's surfaces) graphic representation
of functions of complex variable.
At present programs are created and dynamic characteristics of practically all known by domestic publications RK-methods of implicit and explicit RK-methods are calculated. Design of methodics and program for calculation of dynamic characteristics of methods like Adams' is being completed.
Let us mark two rather important features of dynamic characteristics.
At first, surfaces
are crossed with plane of parameters 
exactly on boundaries 
(see further fig.1) of traditionally known areas of
stability of numerical methods, and within them have negative values. Thus
we have new and rather simple way of constructing areas of stability of
numerical methods. Mark, also, that this way allows to confirm hypothesis
[4] and establish fact of existance (not rare)
of methods with multilinked areas of stability.
At second, using real and imaginative dynamic characteristics and comparing
them to values of respectively 
and 
, we
may construct on the same plane
not only areas of stability, but areas 
,
called areas of dynamic 
correspondence
of numerical methods (see fig.1). Practical importance of application of
these areas is that if all 
of continious model (ODE system), that will be called working points of
algoithmic model, are within this area, then algorithmic model in dynamic
relation will be garanteed to be 
adequate
[10] to continious model (object) with
exactness up to 
.
The shown results of dynamic theory of errors define not the last and now not the most difficult of "underwater stones" of numerical methods of ODE discretization. They have one more important property, to characterize which the following statement is formulated and proved
STATEMENT. Practically all numerical methods of ODE dicretization under certain circumstances are able to significantly change (revolt) the structure of fundamental matrix (system of solutions) of integrated ODE system.
But this means that algorithmic model under such conditions appear to be a model of absolutely different ODE system or object.
In case of Adams methods the statement is trivial. Really, ODE system
of n-th order is transformed by implicit or explicit method of
s-th order to a system of difference equations of respectively n
s
-th or n(s
-1)-th order. Here change of structure of algorithmic model in respect
to ODE system is defined by the essense of these methods and is introduced
into the model intensionally.
In case of RK-methods dimensions and structures of algorithmic model and ODE system coinside and seem to cause no problems. Nevertheless just here the specific property of numeric methods, defined in the statement, is displayed. Now we pass to prove of the statement.
Function of stability of numerical method is function
(), which
may be [6] any of own values of matrix L of ODE system, i.e. function of
stability is always defined on spectre of matrix L. In this case [2,5]
by substitution in it of matrix L instread of
matrix function 
is correctly defined, that is here the matrix R of algorithmic model
for integrated ODE system.
The structure of fundamental matrix of ODE system is defined by normal
Jourdan form of matrix L, that is in its turn defined by complete
system of its elementary divisors. But ODE system at numerical integration
is transformed to system of difference equations with matrix .
Then according to theorem 2 (see [5], p.188),
if L has own values 
and 
-
function, for which 
(i = 1, ..., s), then
elementary divisors
are obtained by substitution of divisors 
of matrix L by expressions 
.
If L has elementary divisor 
and 
, 
then at transition from L to
it is splitted to elementary divisors [5]
where
and symbol 
designates maximal integer, not exceeding 
.
But thus the structure of Jourdan form of matrix R will change in respect to Jourdan form of matrix L of ODE system.
Let us mark that structure of Jourdan form of matrix G (see (2))
exactly corresponds to the changed structure of Jourdan form of matrix
R, despite that 
,
because [2] here 
.
EXAMPLE 3. Let L has one elementary
divisor 
.
One 55 Jourdan
cell corresponds to it and a cell of the same size of fundamental matrix
of ODE system (see textbooks on ODE). Let this system be integrated by
2-stage RK-method (of Euler-Koshy) with step h = 0.5. Let us find
elementary divisors of matrix R of algorithmic model.
Function of stability of this method 
and hence 
.
For these conditions (=
-2, h = 0.5) we have 
, 
(!), 
.
It means that elementary divisor
is splitted in R into elementary divisors (14), where when 
, 
,
according to (15) we have 
, 
.
This way, elementary divisor
of matrix L is splitted in R into elementary divisors 
and 
.
By these results it is easy to set corresponding change of structure of
fundamental matrix of ODE system at its numerical integration.
Let us mark the following circumstance. At present some specialists,
working with models, apply functions of sensitivity to choose optimal step
of integration to minimize errors of modelling. But h is equal in
rights with
argument of stability function (3). Moreover, initially [6] the latter
were received as characteristic polinoms of difference equations 
+ (non-uniform members) for complete error of numerical methods,
in which h is included only in 
.
Therefore it is easy to see, in connection with the numerical methods property
discussed, that incorrect application of functions of sensitivity for the
aims noted before may lead to results that are directly opposite to expected
ones.
Concluding considering this property of numerical methods, let us pay
special attention to the following remarkable fact. If
all working points ()
of algorithmic model are situated within area of of
dynamic correspondence
of method of ODE discretization, then no changes (disturbances) of structure
of fundamental matrix of ODE occur, even if 
is equal to dozens of percents.
The suggested new way represents universal algorithm of constructing
methods of ODE discretization, that are further development of RK-methods,
but more perfect in their properties. We shall give its properties and
advantages of new methods in comparison, for that we shall give a brief
analysis, according to known publications, of the state of this question,
and then - characteristics of new way and advantages of new methods of
ODE discretization, that we shall call K-methods.
For explicit RK-methods dependency of maximally achievable order of accuracy p and necessary for it number of stages s has form of the following table [6,9]:
"The highest order, actually achieved for explicitly constructed ERK-methods is equal to 10 (Guinness' records book, p.333)." ([8], p.203).
"Achievement of formules of still higher orders becomes a complicated problem, making a challenge for mathematicians, difficulties grow more than exponentially, and methods become huge monsters, making step length control still more and more complicated." ([8], p.206).
Table (16) shows that before p = 4 complete correspondence
of p and s is provided. Further so called "Butcher's barriers"
start working, that were formulated by him as theorems (see [8],
pp.202, 203), that state that: when p 
5, no explicit methods of order p exist for s
= p; when p
7, no explicit RK-methods of order p exist for s = p
+ 1; when p
8, no explicit RK-methods of order p exist for s
= p + 2.
We should outline that "... Butcher tried for several years to find explicit 10-stage method of the 8th order" ([3], p.99).
Curtis built 9-stage method of the 8th order of accuracy [1].
It is natural to expect that area of stability of this method exceeds by
its size areas of stability of methods of lower orders of accuracy. However
analysis of errors of Curtis' methods demonstrates quite oppsite effect.
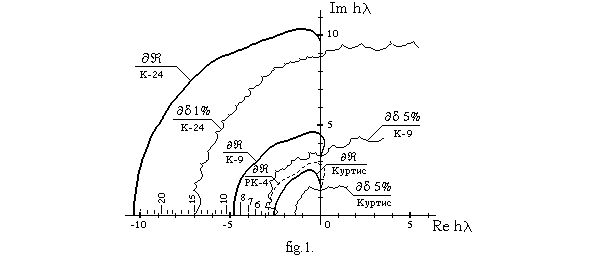
It is displayed in fig.1, where boundaries of area
of stability of classic RK-method (/
RK-4), areas of stability (/
Curtis) and 5% correlation
(5% / Curtis)
of Curtis method.
From formulas of 10th order of accuracy we can extract Hairer method (1978), that has 17 stages [8]. For its creation complete arsenal of simplification conditions of Butcher was applied [3,6]. Coefficients of method are not rational numbers, because they are built on base of quadrature formula of Lobatto of the 10th order.
For dreams about further increase of accuracy of methods the words by
H.Shtetter and theorem ([9], p.176) may be applied,
"The fact that RK-procedures of arbitrary high orders exist at all, is
not too difficult to settle. Theorem 3.3.9. There exist (explicit) RK-procedures
of arbitrary high order". We may notice here, ourselves, that there are
no examples of such procedures.
We shall outline specially that time of calculation of coefficients of K-methods (Butcher table (1)), even when p = s > 120, is equal to parts of second of computer time.
Adjacent on the order of accuracy K-methods may be represented as analogues of known enclosed methods. It allows to build programs of numerical solving of ODE with automatic choice of integration step on their base. Moreover, if during process of ODE solving further shortening of step in its automatic choice is limited by errors of rounding or time resources for solving concrete task, we may, by calling procedure of constructing of Butcher table of higher order of accuracy (taking into account the time for its constructing, mentioned above), continue to solve ODE by the new method, without further shortening of integration step. As a result, the new way of constructing K-methods allows to construct programs of numerical ODE solving with automatic choice of not only step, but the order of accuracy of method as well.
The important advantage of simplicity of constructing of K-methods is possibility of their implementation on hardware level in mathematical coprocessors or computer specprocessors.
Another characteristic of K-methods is that sizes of areas of
stability and correlation,
starting with p = s = 5, and at least, up to
p = s = 24, grow approximately proportionally
to p. In fig.1 by strokes over axis 
only real intervals of stability are denoted, digitizing of which corresponds
to the order of accuracy p of K-methods. Here complete boundary
of area of stability and boundary 
1%
of area of 1% correlation
of K-method of the 24th order (K-24) are shown. It is remarkable also that
area (with boundary 5%)
of 5% correlation
of method K-9 (p = s = 9) completely covers
all area of stability of Curtis method. Taking this into consideration,
as well as some features of K-methods, it is easy to show that method
K-9 is more that twice as efficient as Curtis method.
Complete difiniteness concerning errors of K-methods and high
accuracy (value of area of dynamic correlation)
allow to confidently consider solving ODE systems with arbitrary right
parts and, what is more important, stiff problems. As for the latter, K-methods
are in our opinion more efficient than A-stable implicit RK-methods. This
is caused by that, at first, explicit methods do not require solving systems
of nonlinear algebraic equations at every step (numerical methods of their
solving introduce additional errors), and, at second, left openness of
stability area of implicit RK-methods do not completely guarantee accuracy
of reproducing of dynamics of the ODE system being solved, that is shown
earlier in example 2.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|