А.В.Костельцев.
Россия, Санкт-Петербург,
E-mail: kx@peterlink.ru
Home page: http://private.peterlink.ru/kx/

Интерпретатор Дифференциальных Моделей (IDM)

Для практического исследования возможностей методов и алгоритмов, разрабатываемых авторами в целях создания системы автоматизации моделирования, построен интерпретатор языка программирования, позволяющий решать системы обыкновенных дифференциальных уравнений (ОДУ) разрешенных относительно вектора старших производных. В дальнейшем условимся называть упомянутый язык языком К.

Язык К позволяет описывать системы ОДУ практически в привычной для математиков текстовой форме, например, в форме

dx/dt = a11*x + a12*y;
dy/dt = a21*x + a22*y;

или

x' = a11*x + a12*y;
y' = a21*x + a22*y.

Таким же образом описываются начальные условия и коэффициенты системы ОДУ. При этом начальные условия и коэффициенты могут задаваться как константами, так и в виде отдельных формул и цепочек формул с применением элементарных математических функций и констант, по которым IMD выполняет необходимые вычисления перед началом и в процессе интегрирования системы ОДУ с помощью выбранного численного метода.

IMD может рассматриваться как система автоматизации построения программных моделей динамических объектов или систем по их математическим моделям, заданным в виде систем ОДУ. Как программная среда IMD имеет в своем составе следующие средства:

Компилятор исходного текста математических моделей с языка К во внутримашинное представление программной модели.
Интерпретатор команд внутримашинного представления программной модели
Набор утилит (процедур) компоновки основных функциональных блоков программной модели и алгоритма "существования" модели в рамках заданного модельного "времени".
Процедуры преобразования математических моделей.
Средства работы с библиотеками численных методов.
Процедуры квалиметрии моделей и средства сопутствующих расчетов.
Графическая оболочка для организации взаимодействий с пользователем.

Основная диалоговая панель IMD с загруженной программой (программа приведена полностью в конце данного текста) показана на рис.1 и представляет собой шаблон для ввода основных компонент модели (если говорить о численном решении ОДУ, то речь идет о постановке задачи Коши). Окна, предназначенные для ввода текста, можно развернуть на весь экран. Пользователю предлагается в практически естественной текстовой форме задать следующие элементы.

1. Математическая модель. Текст системы ОДУ записывается в боксе model и компилируется в набор функций расчета правых частей системы ОДУ согласно количеству уравнений в системе.

2. Коэффициенты. Переменные коэффициенты и другие величины, требующие обновления на каждом шаге интегрирования, вводятся в виде текста (бокс coefficients) аналогичным с моделью способом. Главное отличительное свойство блока коэффициентов состоит в том, что его текст компилируется в отдельную функцию, которая в процессе счета будет вызываться перед осуществлением каждого шага интегрирования.

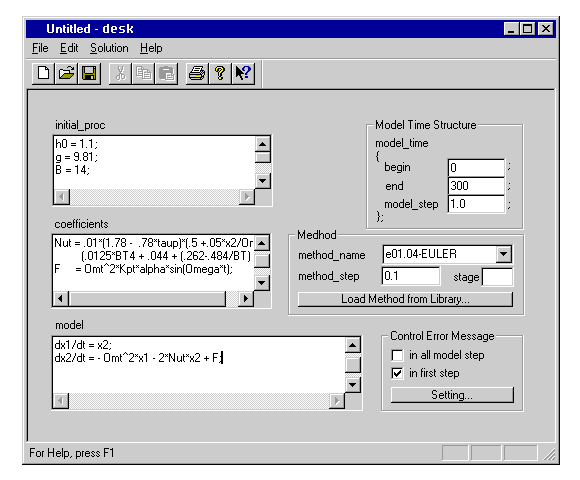Рис.1. Основная диалоговая панель IMD (отладочный стенд).

3. Начальные условия. Могут задаваться в виде простых операторов присваивания (например, x = .5; y = 2.e+37;, и т.п.) или же в виде математического алгоритма их расчета. Пользователь вводит начальные условия, в специально отведенный шаблоном текстовый бокс (initial_proc). Его содержимое компилируется затем в отдельную функцию инициализации модели. Данная функция вызывается на выполнение один раз перед началом интегрирования системы ОДУ (имитации поведения модели). Следует отметить, что в блоке задания начальных условий можно определять любые величины (переменные), в том числе и постоянные коэффициенты математической модели.

4. Метод численного интегрирования. Выбирается пользователем из встроенной или предварительно записанной пользователем в память ЭВМ собственной библиотеки методов. Встроенный библиотекарь IMD построен таким образом, что предоставляет пользователю не только способ хранения методов, но и дает возможность исследовать, при необходимости, их динамические свойства. Процедуры, входящие в состав библиотекаря позволяют рассчитывать и наглядно представлять динамические характеристики, области устойчивости и области динамической согласованности методов. Это, в свою очередь, дает возможность вполне обоснованно выбирать из библиотеки как сам метод дискретизации ОДУ, так и оптимальный шаг интегрирования для данной математической модели.

Метод как программный объект является набором данных для встроенной процедуры численного интегрирования (многократного расчета правых частей ОДУ).

5. Модельное время. Задается начало, конец и шаг модельного "времени". Здесь под интервалом модельного "времени" (начало – конец) понимается общий интервал изменения независимой переменной системы ОДУ. Заметим, что решаемая система ОДУ должна быть автономной. Это требование, однако, практически не сковывает пользователя, т.к. перевод любой неавтономной системы в соответствующую автономную легко осуществляется добавлением простого уравнения (например, dx/dt = 1 ) и введением новой независимой переменной. Создаваемая модель в процессе своего функционирования взаимодействует с окружающей средой на каждом шаге модельного "времени". Простейшим примером такого взаимодействия может служить передача текущих значений переменных состояния модели на печать. Если говорить о многомодельной среде, то шаг модельного времени определяет моменты взаимодействия "живущих" одновременно моделей между собой.

Заметим здесь, что шаг модельного времени и выбранный пользователем шаг дискретизации системы ОДУ не обязаны не только совпадать друг с другом, но и быть когерентными.

Модельное время, после компиляции во внутреннее представление становится некоторой структурой глобальных данных, к которым может обращаться любой функциональный блок модели. Иначе говоря, текущее модельное время всегда доступно (по имени независимой переменной) в любой точке исходного текста модели.

На этом работа пользователя по созданию программной модели заканчивается.

В заключение приведем пример конкретной программы, построенной путем заполнения шаблона, предлагаемого IMD. Такие программы строятся автоматически и при их дальнейшем использовании IMD автоматически загружает и интерпретирует подобные тексты. Пользователю не обязательно знать эту форму представления программ для IMD, но для более четкого понимания принципов построения программных моделей полезно иметь представление о структуре исходного текста таких программ.

DIFFERENTIAL EQUATIONS SET PROGRAM "@(#)VMFRK1_1.K 01.00 96/07/31";
%{
символы %{ и %} ограничивают текстовое описание модели, вводимое пользователем в специально отведенный бокс как коментарий.

   h0    - начальная поперечная метацентрическая высота (м);
   g     - ускорение свободного падения (9.80665 м/с^2);
   B     - ширина корабля (м);
   T     - осадка корабля (м);
   L     - длина корабля (м);
   Sk    - площадь скуловых килей (м^2);
   ks    - коэффициент для расчета площади сечения корабля (.715);
   Swl   - площадь сечения корабля (м^2);
   Skwl = Sk/Swl; - отношение площадей (.03);
   Omt   - частота собственных бортовых колебаний (.598 рад/с);
   tau   - период собственных бортовых колебаний (с);
   taup = tau*sqrt(g/B); - приведенный период;
   alpha - угол волнового склона (рад); [задается 4.5 и 9.0 град.]
   Omega - частота возмущения
           [.3, .4, .5, .55, .6, .65, .7, .8, .9, 1.0, 1.1](рад/с);
   teta - угол
           в уст.режиме [13,15, 20, 25, 30, 25, 20, 10, 5, 4, 2](рад);
   tetap - угловая скорость (рад/с);
   r     - поперечный метацентрический радиус (3.65 м);
   Hi    - коэффициент вертикальной полноты (.699);
   R     - обобщенный параметр корабля;
           { R = Hi/sqrt(2*PI*g)*Omega*(B*T*Hi*r/h0)^.25; }
   Kpt   - редукционный коэффициент возмущающего момента;
           { Kpt = exp(-4.2*R^2); }
%}

model_time
{
interval = [0 ... 300] 1;
independent_variable t;
};

method
{
name = "e01.04_EULER";
step = 0.1;
};

initial_proc()
{
   h0   = 1.1;
   g    = 9.81;
   B    = 14;
   T    = 4.8;
   L    = 132.;
   Sk   = 40.;
   ks   = .715;
   Swl = B*L*ks;
   Skwl = Sk/Swl;

   Omt = .598;
   tau = 2*PI/Omt;
   taup = tau*sqrt(g/B);

   alpha = 9.*PI/180;
   Omega = .3;
   teta = 13.*PI/180.;
   tetap = teta*Omt;

   r   = 3.65;
   Hi = .699;
   SQ4 = (B*T*Hi*r/h0)^.25;
   RX = Hi/sqrt(2*PI*g);
   R   = RX*SQ4*Omega;
   R2 = R^2;
   Kpt = exp(-4.2*R2);

   BT = B/T;
   BT4 = BT^4.;
   Bh = B/h0;

x1 = teta;
x2 = tetap;
}

coefficients()
{
Nut = .01*(1.78 - .078*taup)*(.5 + .05*x2/Omt)*
(.0125*BT4+.044+(.262-.484/BT)*Skwl)*Bh*Omt;

F = Omt^2*Kpt*alpha*sin(Omega*t);
}

model()
{
dx1/dt = x2;
dx2/dt = -Omt^2*x1 - 2*Nut*x2 + F;
}

print x1, x2, Nut, F;

Ядро данного интерпретатора полностью переносимо, первый интерфейс был написан для OS/2. Сейчас автор находится в процессе написания мультисинтаксического компилятора языка моделирования поддерживающего (кроме ОДУ) языки разностных уравнений, схемы аналоговых вычислительных машин и т.д., кроме того язык будет обладать мощью обычных языков программирования (С).

Site of Information Technologies
Designed by inftech@webservis.ru.