 |
||
2. Моделирование обучаемых систем управления
Основой моделирования обучаемых систем управления является разработка математической модели процедуры ее обучения.
2.1. Математическое моделирование процесса
обучения обучаемой системы управления2.1.1. Алгоритм обучения обучаемой
системы управления Процесс обучения, заключающийся в формировании проводимостей регулируемых резисторных элементов преобразующей матрицы, аналогичен формированию условных рефлексов в живой природе. Если в какой-либо ситуации сигнал управления отдельным исполнительным органом не удовлетворяет обучателя, он подает обучающий сигнал на соответствующий столбец резисторной матрицы. Это можно осуществить, например, нажимая кнопку из токопроводящей резины, в виде которой выполнен элемент коммутации распределителя сигналов обучения. Чем сильнее усилие нажатия кнопки, тем больше значение обучающего сигнала, подаваемого на соответствующие преобразователи проводимостей резисторных элементов. При этом может исказиться сигнал управления данным исполнительным органом в другой ситуации. Его аналогично корректируют до требуемой величины. Затем переходят к следующей ситуации, соответствующей очередному шагу обучения. Проведя обучение во всех ситуациях обучаемой выборки, снова возвращаются к первой и т.д. Как говорится, повторение – мать учения.
Примем, что в любой ситуации сигнал управления отдельным исполнительным органом определится как

где
j – номер ситуации; m – общее количество рецепторов; bij – возбуждение i-го рецептора в j-ой ситуации; ci – весовой коэффициент i-го рецептора.D ci = Kj · D Ej · bij ,
__________________(2.2)где
Kj – общая команда на корректировку в j-ой ситуации.Если задаться целью сведения ошибки D
Ej после обучения на данном шаге к нулю, то очевидно
Команда
Kj определится из совместного решения (2.2) и (2.3):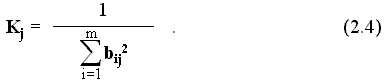
Подставляя (2.4) в (2.2), получим выражение для определения поправки весового коэффициента каждого рецептора

Таким образом, на каждом
t-м шаге обучения значение i-ого весового коэффициента определится выражением: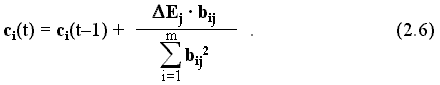
Выражения (2.1) и (2.6) составляют вычислительную модель обучаемой системы управления. Вычислительная модель может использоваться в качестве универсального алгоритма управляющих вычислительных машин (микропроцессоров и в том числе ЧПУ), работающих в режиме обучаемых систем управления.
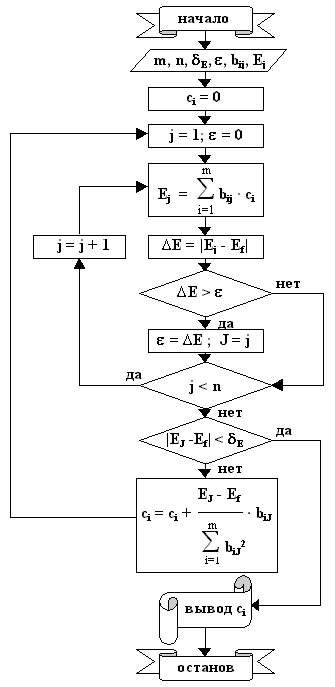
Схема алгоритма расчета весовых коэффициентов представлена на рис.2.1. В блок-схеме алгоритма
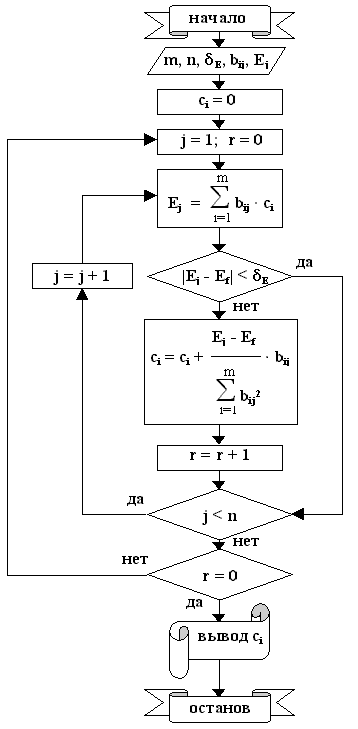
Рис.2.1. Алгоритм расчета весовых коэффициентов
С математической точки зрения данный алгоритм (рекуррентный алгоритм Качмажа) не самый оптимальный по числу необходимых итераций. Однако особенность его в том, что, как здесь было показано, он вытекает из процедуры обучения и отражает реальный процесс обучения обучаемых систем, в том числе и биологических. Другими словами, использование данного алгоритма в обучаемых системах определяется не выбором его из многих возможных, а является результатом математической формализации процедуры обучения.
2.1.2 Алгоритм расчета рецепторных
долей сигнала управленияНастройка проводимостей резисторных элементов матрицы технического мозга может быть неудобной в том случае, когда нет возможности изолировать каждый такой элемент. В этом случае предпочтительным является настройка, основанная на коррекции долей сигнала управления eij, определяемых отдельными рецепторами:
eij = ci · bij .
_____________________(2.7)Сигнал управления при этом рассматривается как сумма долей сигналов всех рецепторов:
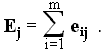
С учетом того, что поправка
D cij проводимости i-го элемента технического мозга в j-ой ситуации зависит от погрешности сигнала управления D Ej и от возбуждения соответствующего рецептора bij , имеемD cij = K · D Ej · bij
.Поправка доли D
eij сигнала управления определится какD eij = D cij · bij = K ·
D Ej · bij2 .Учитывая, что сумма поправок долей должна полностью устранять погрешность сигнала управления в данной ситуации на
t-ом шаге обучения, получим аналитическое выражение для расчета элементарных рецепторных долей сигнала управления: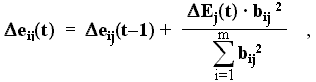
где
t – номер данного шага обучения. Полученное выражение позволяет рассчитать доли сигнала управления от отдельных рецепторов в некоторой опорной ситуации, что позволяет настроить матрицу технического мозга в этой ситуации так, что он будет формировать правильные сигналы управления во всех ситуациях обучаемой выборки.
Доли сигналов управления удобно пересчитывать относительно некоторой опорной ситуации, в которой затем осуществляется настройка матрицы мозга. В качестве опорной может
Порядок расчета долей сигнала управления следующий.
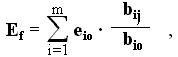
где индекс "о" означает опорную ситуацию
.2. Определяют ошибку сигнала управления в этой ситуации:
D
Еj = Еj – Еf.3. Проверяют условие
D
Еj < d E j ,где d
E j – допустимое отклонение сигнала управления Еj . Если условие соблюдается, то предъявляют следующую ситуацию обучаемой выборки; если условие соблюдается во всех ситуациях обучаемой выборки, то расчет прекращают.4. Если условие не выполняется, то уточняют значения долей сигнала управления в пересчете на опорную ситуацию по формуле
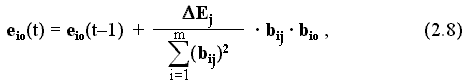
Полученные в результате расчета значения долей сигналов управления используют для настройки резисторной матрицы технического мозга. Для этого системе предъявляют ситуацию, выбранную в качестве опорной, и изменяют проводимости соответствующих резисторных элементов таким образом, чтобы получить от каждого расчетное значение его доли сигнала управления.
2.1.3. Условие сходимости процесса обучения
Как видно из формулы (2.6), алгоритм обучения представляет собой вариант решения системы линейных алгебраических уравнений, известный как рекуррентный алгоритм Качмажа. При этом формулу (2.1) можно представить в виде:
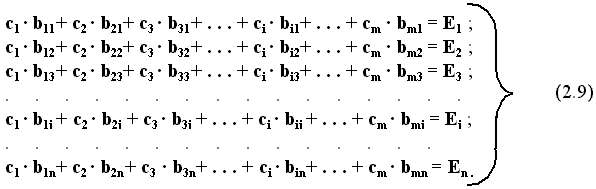
Если система уравнений (2.9) совместна, то данный алгоритм приводит к ее решению, т.е. определению весовых коэффициентов
ci , обеспечивающих заданные выходные сигналы обучаемой системы Ej во всех ситуациях обучаемой выборки, характеризуемых признаками bij .Далее следует отметить, что в реальных технических системах сигналы управления задаются с некоторым допуском, т.е. допустимым отклонением от номинального значения, причем величина этого допуска в некоторых ситуациях может быть значительной, вплоть до того, что задается только знак сигнала, положительный или отрицательный. Итак, сигнал управления в
j-ой ситуации задается в пределах, определяемых выражениемEj – d Ej
(–) £ Ej £ Ej + d Ej(+) ,где d
Ej(–) – нижнее отклонение сигнала управления в j-ой ситуации, d Ej(+) – верхнее отклонение сигнала управления в j-ой ситуации.
2.2. Закономерности процесса обучения, выявленные
с помощью его математической модели2.2.1. Закономерности процесса обучения системы
управления для двух ситуаций обучаемой выборкиРассмотрим процесс обучения системы управления формированию выходных сигналов E1 и E2, соответствующих ситуациям A1 и A2, представленных образами B1 и B2 с наборами признаков:
B1
: ___ b11, _b21, _b31, _ . . . , _bm1 ;Для определения закономерностей процесса обучения используем вычислительную модель обучаемой системы управления [6
1 – 68]. Обучение состоит в поочередном предъявлении ситуаций с корректировкой весовых коэффициентов признаков. Каждое предъявление ситуации – шаг обучения, поочередное предъявление всех ситуации – цикл обучения. На каждом шаге p обучения весовые коэффициенты корректируются в соответствии с выражением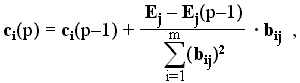
где
ci(p) – весовой коэффициент i-го признака на p-м шаге обучения; ci(p–1) – значение весового коэффициента i-го признака на предшествующем шаге обучения; Ej(p–1) – значение выходного сигнала в j-ой ситуации, определяемое весовыми коэффициентами, полученными после p–1 шага обучения. Начальные значения весовых коэффициентов (до начала обучения) приняты равными нулю.Величина абсолютной ошибки формирования выходного сигнала на
t-ом цикле обучения определится выражениемD Ej(t) = Ej – Ej(t) ,
где
Ej(t) – значение j-го выходного сигнала на t-ом цикле обучения.D E1(1) = E1 – E1(1) .
Фактическое значение выходного сигнала для первой ситуации на первом цикле обучения:
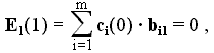
т.к. начальные значения весовых коэффициентов
ci(0) = 0 .D E1(1) = E1 .
Для второй ситуации:
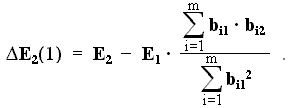
На втором цикле:
D
E1(2) = – Z12 · (E2 – E1 · Z21) ,
D
E2(2) = (E2 – E1 · Z21) · (Z21 · Z12) ,
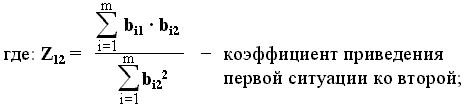
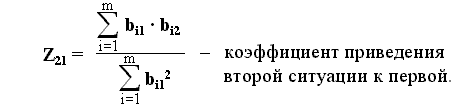
На последующих циклах обучения величины абсолютных ошибок выходных сигналов определяются выражениями
D E1(t) = – Z12 · (E2 – E1·Z21) · (Z21·Z12)t–2 ,
_________________(2.10)Анализ выражений (2.10) и (2.11) показывает, что скорость обучения выработке выходных сигналов для двух ситуаций зависит от соотношения величин требуемых сигналов
E1 и E2 и от значений коэффициентов приведения образа первой ситуации к образу второй – Z21 и образа первой ситуации к образу первой – Z12.Величина, определяемая выражением
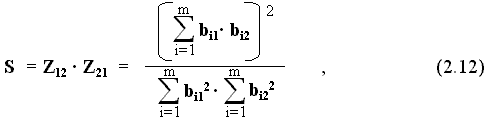
характеризует степень сходства (совпадения) двух образов и не может быть больше единицы.
D = 1 – S
,характеризует степень отличия (различия) двух образов.
Если соответствующие признаки образов полностью совпадают или отличаются друг от друга в одной и той же пропорции, то
S=1, при этом обучение возможно только в случае, если требуемые выходные сигналы отличаются в той же пропорции, что и их признаки. В общем случае S<1, и, чем меньше значение S, тем быстрее идет обучение. При S=0, когда для всех признаков двух образов ситуаций один из соответствующих друг другу признаков имеет нулевое значение (полное отличие образов), для обучения достаточно одного цикла. В терминах векторной алгебры, степень совпадения двух образов равна квадрату косинуса угла между векторами B1 (b11, b21, b31, ... , bm1) и B2 (b12, b22, b32, ... , bm2).С учетом (2.12) выражения (2.10) и (2.12) примут вид:
D E1(t) = – Z12 · (E2 – E1·Z21) · S t–2 ,
______________________(2.13)Из выражений (2.13) и (2.14) можно определить необходимое для обучения число циклов, если задаться допустимыми отклонениями формирования выходных сигналов d
E . При симметричном допуске на выходные сигналы обучение можно считать законченным, когда для всех образов значения абсолютных ошибок сигналов будет отвечать условию: D E £ d E / 2 . Тогда число циклов находится из выражений: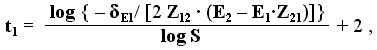
или:
t1 = logS
{ – d E1/ [2 Z12 · (E2 – E1·Z21)]} + 2 , _________(2.15)где d
E1 и d E2 – допустимые отклонения формирования выходных сигналов для первого и второго образов, симметричные относительно номинальных значений.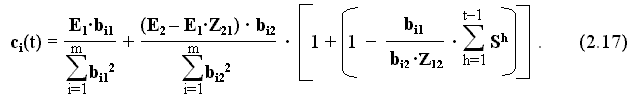
Зная необходимое число циклов обучения, значения признаков и требуемых выходных сигналов двух образов, по формуле (2.17) можно вычислить значения весовых коэффициентов всех признаков образов, обеспечивающих заданную точность формирования выходных сигналов.
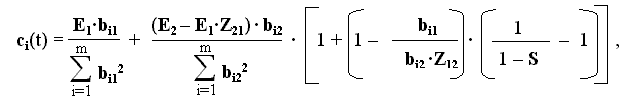
другими словами, для двух образов, степень отличия которых:
D>0, – процесс обучения сходится всегда.
2.2.2. Закономерности процесса обучения системы управления
при последовательном предъявлении ситуацийПроцедура обучения состоит в поочередном предъявлении ситуаций обучаемой выборки, причем каждое предъявление ситуации – это шаг обучения. На каждом шаге обучения происходит корректировка проводимостей резисторных элементов преобразующей матрицы. Обучение может быть циклическим, когда предъявление ситуаций обучаемой выборки повторяется в одном и том же порядке до конца обучения. Может быть установлен и любой другой определенный порядок предъявления ситуаций. Кроме этого, обучение может быть произвольным (неупорядоченным), когда порядок предъявления ситуаций не устанавливается и может носить случайный характер.
Допустим, для обучения робота с обучаемой системой управления использовалось N ситуаций, составляющих обучаемую выборку. Обучение закончилось за M шагов. Для определения закономерностей процесса обучения будем рассматривать обучение не как циклическое, произвольное или с заданным порядком предъявления ситуаций, а как последовательное предъявление M ситуаций. Такое представление включает в себя все многообразие возможных процедур обучения. Кроме этого, реально при обучении методом “вождения за руку” ситуации абсолютно точно могут и не повторяться вообще, однако такое обучение возможно, и его можно считать последовательным. Далее обучение может идти с учетом фактора времени, т.е. в систему очувствления могут быть включены датчики времени, и уже поэтому такие ситуации не могут повториться (как говаривал Гераклит: “Нельзя дважды войти в одну и ту же реку”). Такое обучение может быть только последовательным. В связи с этим следует отметить, что обучение биологических систем (выработка условных рефлексов), строго говоря, – последовательное [67].
Можно показать, что, исходя из формул алгоритма обучения, величина фактического сигнала управления по шагам обучения будет изменяться следующим образом.
Примем исходные значения весовых коэффициентов равными нулю, тогда на первом шаге обучения получим фактическое значение выходного сигнала E1(f) = 0.
После корректировки весовых коэффициентов на этом шаге обучения получим выходной сигнал, равным
E1.Фактический выходной сигнал на втором шаге обучения будет определяться весовыми коэффициентами, полученными после первого шага обучения и равными
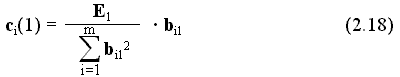
в соответствии с формулой

Подставив (2.18) в (2.19), получим
E
2(f) = E1·Z21 ,где
Z21 – коэффициент приведения второй ситуации к первой.E
3(f) = E2 ·Z32 + E1· (Z31 – Z21·Z32) ,где
Z31 – коэффициент приведения третьей ситуации к первой,На четвертом шаге обучения:
E
4(f) = E3 ·Z43 + E2 · (Z42–Z32 ·Z43) + E1 · (Z41 – Z21 ·Z42 – Z31 ·Z43 + Z21 ·Z32 ·Z43) ,На пятом шаге обучения:
E
5(f) = E4 ·Z54 + E3 · (Z53 – Z43 ·Z54) + E2 · (Z52 – Z32 ·Z53 – Z42 ·Z54 + Z32 ·Z43 ·Z54) +и т.д.
Число членов с одинаковым числом сомножителей
Z в скобках соответствует числам так называемого треугольника Паскаля, каждое из которых получается сложением соседних чисел вышестоящей строки:1
1
Так число членов с одинаковым числом сомножителей
Z в скобках четвертого слагаемого соответствует четвертой строке треугольника Паскаля.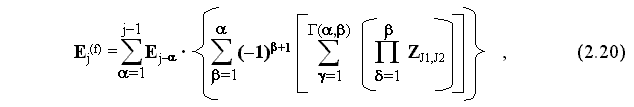
где Г(a
,b ) = 1 при a =1, при b =1 и при a =b ;
Индексы
J1 и J2 чередуются определенным образом, охватывая ситуации в интервале от j–a до j . Формула (2.20) показывает, что фактический сигнал управления в некоторой ситуации зависит от всех предшествующих ситуаций, в которых происходила корректировка весовых коэффициентов: как от возбуждений рецепторов в этих ситуациях, так и от заданных для них выходных сигналов.
Соответственно, значения весовых коэффициентов при последовательном обучении на
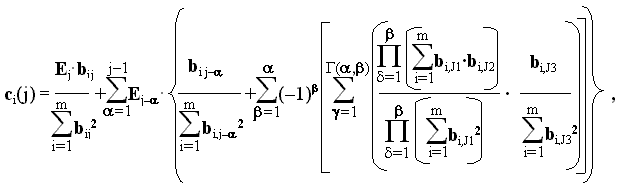
где
Г(a ,b ) = 1 при a = b и при a =1,
2.2.3. Обучение с масштабированием подобных ситуаций
В процессе обучения и работы обучаемой системы управления могут возникать ситуации, соответствующие признаки которых отличаются друг от друга в одно и то же число раз (для двух образов: bi2 = k · bi1). Это возможно, например, при изменении уровня освещенности обозреваемой сцены. Такие ситуации являются подобными, а величина k – отношение подобия этих ситуаций. Обучение формированию сигналов управления исполнительным двигателем, не отвечающих условию: E2 = k · E1, для таких ситуаций невозможно. Для преодоления этого ограничения в изображения этих ситуаций можно искусственно ввести дополнительный масштабирующий признак некоторой постоянной величины, например на дополнительный рецептор подавать постоянный сигнал для всех ситуаций.
Степень совпадения двух ситуаций S определяется выражением 2.12. Для подобных ситуаций S = 1. Оптимальный масштабирующий признак должен быть таким, чтобы значение степени совпадения для данных двух ситуаций стало минимальным. При использовании масштабирования степень совпадения двух ситуаций будет иметь вид
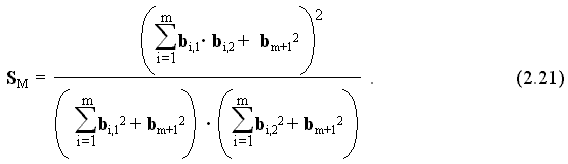
Отсюда следует, что степень совпадения двух ситуаций будет минимальной при
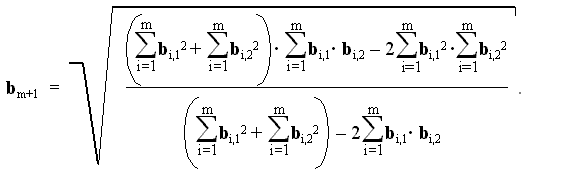
Для двух подобных ситуаций оптимальный масштабирующий признак определится как
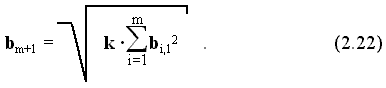
Из выражений (2.21) и (2.22) следует, что минимальная степень совпадения двух подобных ситуаций, достигаемая масштабированием, определяется только отношением подобия
k и связана с ним зависимостьюS
min = 4 k / (1 + k)2 .___________________(2.23)В качестве примера рассматриваются две ситуации, представленные наборами признаков:
B
1: ___ 2 __ 8 __ 1 __ 5 __ 4 __ 7 __ 3 _ 11 __ 9 __ 6 ;Здесь число признаков:
m = 10 , отношение подобия: k = 3 , степень совпадения ситуаций: S = 1 . Оптимальный масштабирующий признак, определенный по формуле (2.22), будет иметь значение bm+1= 34,899857. Степень совпадения для масштабированных ситуацийB
1*: ___ 2 __ 8 __ 1 __ 5 __ 4 __ 7 __ 3 _ 11 __ 9 __ 6 _ 34,899857;в соответствии с формулами (2.21) и (2.23), имеет значение
SM = 0,75 .Кроме формирования отличительности подобных ситуаций, масштабирование может быть использовано и для сокращения длительности обучения, причем не только для подобных ситуаций. Если обучателю известны значения сигналов управления, соответствующие двум ситуациям, то из анализа зависимостей ошибок сигналов управления от числа циклов обучения (2.15, 2.16) может быть найдено значение масштабирующего признака, обеспечивающего минимальную продолжительность обучения. Так, оптимальный масштабирующий признак, определенный по формуле
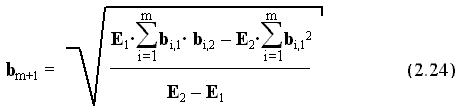
или для подобных ситуаций:
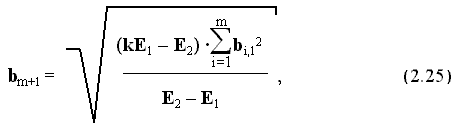
позволяет осуществить обучение за один цикл.
Для двоичных ситуаций, признаки которых могут принимать только два значения: ноль и единицу, – формула (2.24) примет вид
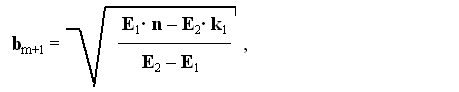
где
n – число совпадающих признаков двоичных ситуаций, k1 – число единичных признаков первой ситуации.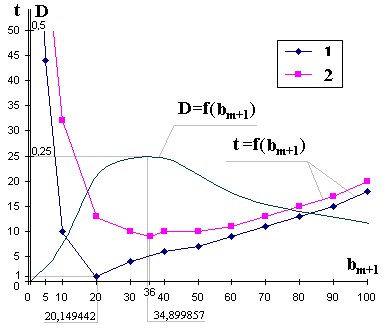
1 – график зависимости t = f(bm+1) для ситуаций с признаками B1 и B2 при E1 = 1 , E2 = 2;
2 – график зависимости t = f(bm+1) для ситуаций с признаками B1 и B2 при E1 = 2 , E2 = 1
Рис.2.2. Зависимость продолжительности обучения от значения
масштабирующего признака для подобных образов
Следует отметить, что масштабирование обеспечивает сходимость процесса обучения для любых двух подобных ситуаций.
2.2.4. Влияние заданной точности выходных
сигналов на продолжительность обученияВажным фактором, влияющим на продолжительность обучения обучаемой системы, является заданная точность формирования выходных сигналов в ситуациях обучаемой выборки.
Методика исследования. Исследование проводилось с использованием математической модели процесса обучения. Обучение проводилось для наборов из пяти образов с числом признаков: m = 10. В качестве значений признаков брались случайные целые числа в пределах от 0 до 9. Значения выходных сигналов принимались равными порядковому номеру образа в наборе: для первого образа E1 = 1, для второго E2 = 2 и т.д. Вначале допустимое отклонение выходных сигналов задавалось в пределах d E = ± 0,01. Затем допустимое отклонение расширялось до d E = ± 0,5 с дискретой, равной 0,01. Для каждого значения d E определялось число шагов обучения, необходимое для получения выходных сигналов с заданной точностью и характеризующее продолжительность обучения.
Полученные результаты. Зависимость продолжительности обучения от заданной точности рассмотрим на примере обучения для семи наборов образов:
1)
___5___0___3___5___8___0___3___8___6___3________E1 = 1;2)
___9___4___6___9___1___4___9___2___4___7________E1 = 1;3)
___8___9___4___6___9___1___4___6___2___4________E1 = 1;4)
___0___3___6___1___3___6___8___1___3___9________E1 = 1;5)
___3___6___8___1___3___9___1___4___6___9________E1 = 1;6)
___2___7___0___3___5___8___0___5___8___0________E1 = 1;7)
_ __9___1___4___6___9___2___7___9___2___4________E1 = 1;В результате исследований получены значения чисел шагов обучения, необходимых для достижения заданной точности, определяемой значениями допусков на выходные сигналы d
E. Эти значения представлены на рис.2.3: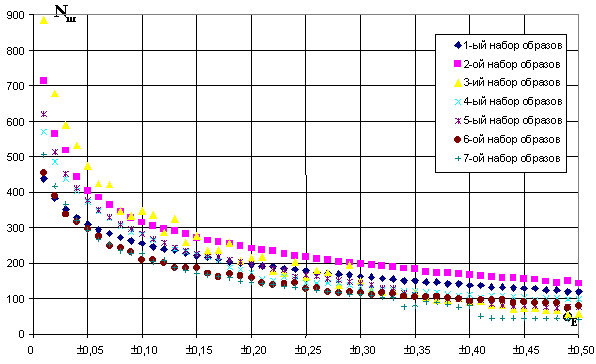
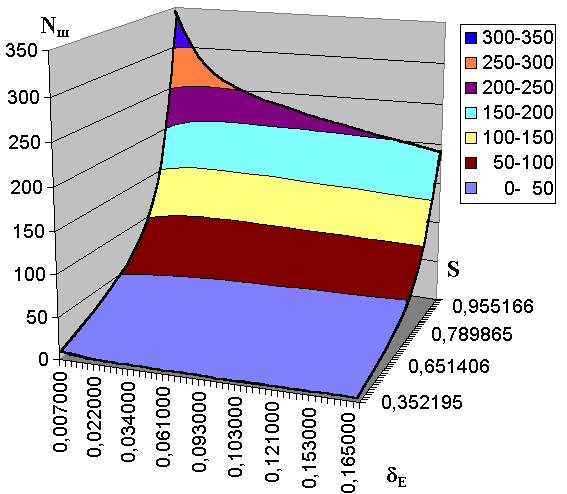
При использовании логарифмической шкалы для заданных значений допусков d
E график примет следующий вид: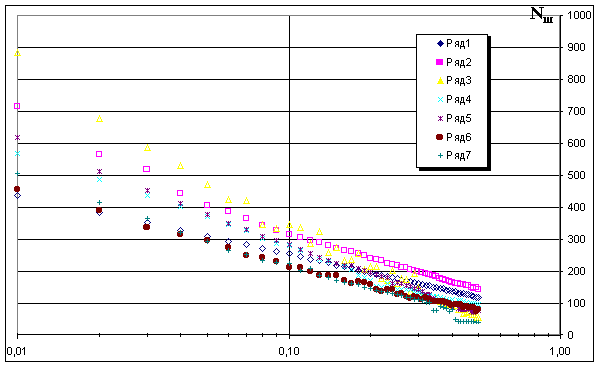
Выводы. Полученные результаты согласуются с формулами (2.15) и (2.16) и подтверждают вывод о том, что число шагов обучения, необходимых для достижения требуемой точности, определяется по логарифмическому закону [62]:
N
ш = K1 – K2 · lg d E ,где
K1 и K2 – постоянные для каждой конкретной обучаемой выборки, определяемые образами выборки и заданными выходными сигналами для них.
2.2.5. Влияние отличительности образов ситуаций
обучаемой выборки на продолжительность обученияМетодика исследования. Влияние отличительности и заданной точности выходных сигналов на продолжительность обучения рассмотрим на примере обучения для двух бинарных образов с числом признаков m = 10. Все признаки одного из образов примем равными единице. Значения признаков другого образа будем изменять следующим образом: вначале только один из признаков зададим равным единице, остальные – равными нулю, затем добавим еще один единичный признак и так далее до девяти единичных признаков второго образа. Число n нулевых признаков второго образа, отнесенное к общему числу признаков m, определяет степень отличия двух данных образов. Для одного из образов выходной сигнал задавался равным единице (E1 = 1), для другого – двум (E2=2), затем требуемые сигналы менялись (E1=2, E2=1). При обучении использовалось три варианта порядка предъявления образов: 1 – обучение начиналось с образа, содержащего нулевые признаки и с заданным сигналом, равным единице; 2 – обучение начиналось с образа со всеми единичными признаками и с заданным сигналом, равным единице; 3 – обучение начиналось с образа со всеми единичными признаками и с заданным сигналом, равным двум (рис.2.5, рис.2.6).
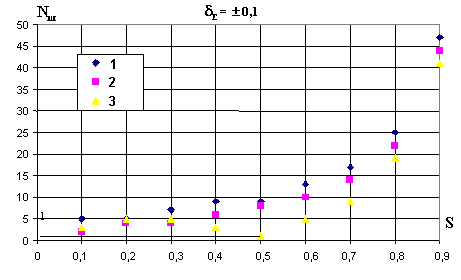
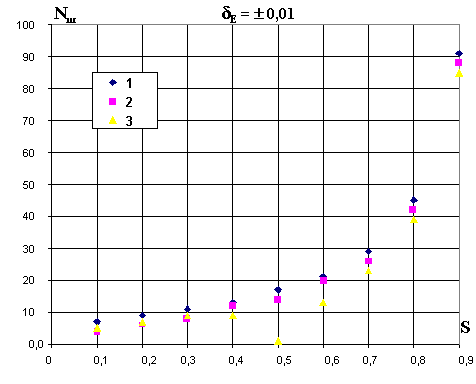
Полученные результаты. В общем случае, чем больше отличительность образов обучаемой выборки, тем быстрее заканчивается обучение до заданной точности, однако определенное соотношение выходных сигналов и отличительности ситуаций приводит к более быстрому обучению, что видно на графиках (рис.2.5, рис.2.6) в точках, после которых дальнейшее увеличение отличительности приводит к некоторому увеличению продолжительности обучения.
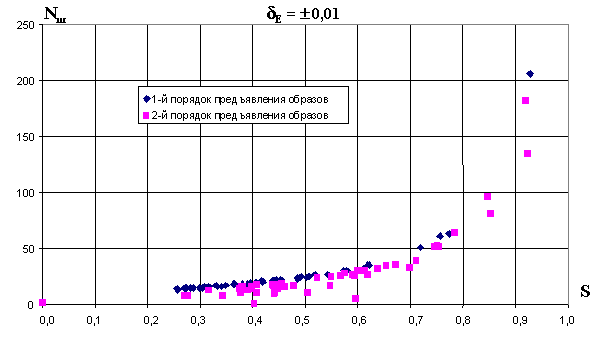
Более четко прослеживается зависимость числа циклов обучения
Nц от степени совпадения образов (рис.2.8).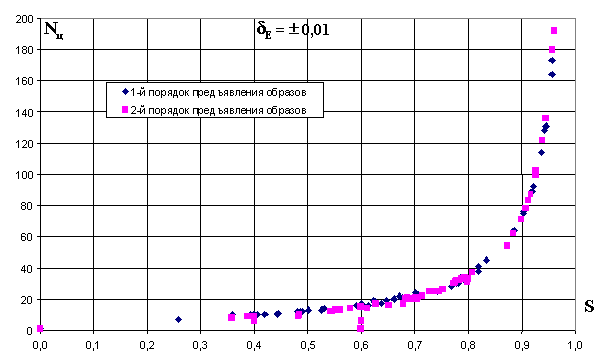
Из графиков видно, что для образов с
S = 0 (полное отличие образов) обучение заканчивается за один цикл. То же самое происходит и для образов, степень совпадения которых S=E2/E1, в нашем случае при S = 0,6 , причем первый образ не должен содержать нулевые признаки, которые во втором образе имеют ненулевое значение. При S, стремящейся к 1, число циклов обучения резко возрастает, а при S = 1 обучение становится невозможным кроме как для образов, отношение подобия которых отвечает условию: E2 = k ·E1 (см. п.2.2.3).Выводы. Система очувствления обучаемой системы управления должна строиться таким образом, чтобы воспринимать как можно больше отличительных признаков в ситуациях, которые возникают при решении требуемой задачи, чтобы степень совпадения образов обучаемой выборки была минимальной, что значительно ускоряет обучение системы.
2.2.6. Влияние порядка предъявления ситуаций
обучаемой выборки на продолжительность обученияАнализ влияния порядка предъявления ситуаций на продолжительность обучения будем проводить с помощью вычислительной модели обучаемой системы управления. В качестве примера рассмотрим два варианта обучения для пяти ситуаций с десятью числовыми признаками (таблица 1).
Таблица 1
|
№ п/п |
Ситуации обучаемой выборки |
Сигналы E |
|||||||||
|
b1 |
b2 |
b3 |
b4 |
b5 |
b6 |
b7 |
b8 |
b9 |
b10 |
||
|
1 2 3 4 5 |
8 ____8____6____3____1____1____6____4____4____27 ____2____0____5____0____7____8____5____3____16 ____3____8____4____1____9____4____2____9____42 ____0____7____2____0____5____3____0____6____18 ____6____4____9____6____4____9____7____4____9 |
1 2 3 4 5 |
|||||||||
Допуск на значения сигналов управления: d
E = ± 0,1 .Первый вариант обучения:
Порядок предъявления ситуаций – циклический. Число шагов обучения, необходимых для достижения заданной точности: 225. Значения полученных в результате обучения весовых коэффициентов признаков:
___ ___
0,277424; __–0,398268; ___0,391117; ___0,294749; ___0,171608;Полученные в результате обучения фактические выходные сигналы в ситуациях обучаемой выборки имеют следующие значения:
______
Ef1=0,943592; ___Ef2=1,931619; ___Ef3=3,079798; ___Ef4=3,940933; ___Ef5=5,000000.Процесс приближения фактических сигналов управления к заданным значениям по шагам обучения при циклическом предъявлении ситуаций представлен на рис.2.10.
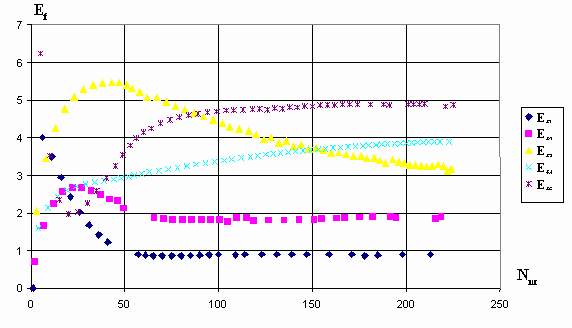
Второй вариант обучения:
При этом варианте после каждого шага обучения определяются значения абсолютных ошибок для сигналов управления во всех ситуациях, и на следующем шаге предъявляют ситуацию, в которой ошибка сигнала управления была самой большой. Обучение до заданной точности закончилось за 153 шага. Значения весовых коэффициентов признаков, полученных в результате обучения:
______
–0,269060; __–0,387141; ___0,392780; ___0,289534; ___0,166311;Полученные в результате обучения фактические выходные сигналы в ситуациях обучаемой выборки имеют следующие значения:
______
Ef1=1,079238; ___Ef2=1,963388; ___Ef3= 3,098165; ___Ef4=3,936747; ___Ef5=5,000000.На рис.2.11 показан процесс приближения фактических сигналов управления к заданным значениям по шагам обучения для второго варианта предъявления ситуаций.
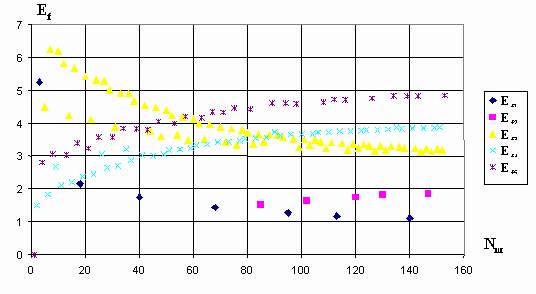
Уменьшение числа шагов обучения при втором варианте обучения носит устойчивый характер, т.е. имеет место при любых образах и заданных выходных сигналах.
Для данного примера число шагов, необходимых для достижения заданной точности при обучении по второму варианту, почти в полтора раза меньше, чем по первому варианту. Значения весовых коэффициентов признаков для двух вариантов близки и при уменьшении допуска на сигналы управления будут еще больше сближаться.
Из приведенных графиков видно, как изменяются значения фактических сигналов управления по шагам обучения: на начальном этапе формируются сигналы управления, которые не соответствуют заданным значениям, затем значения сигналов приближаются к некоторой средней величине, и далее – расходятся, стремясь к заданным величинам до тех пор, пока не войдут в пределы допусков на сигналы управления.
Рассмотренные варианты отражают реальные процессы обучения объектов, оснащенных обучаемыми системами управления. Так, при обучении робота обучатель может, используя метод “вождения за руку”, многократно циклически повторять движения робота в режиме обучения, добиваясь того, что робот будет двигаться с заданной точностью, необходимой для выполнения поставленной задачи. Таким образом реализуется первый вариант обучения. Того же результата обучатель может добиться, если по ходу движений робота будет подавать сигналы коррекции лишь в тех ситуациях, в которых сигналы управления исполнительными двигателями имеют наибольшие отклонения от требуемых значений, т.е.
2.2.7. Влияние способа дробления входной информации
на продолжительность обучения Признаковое представление информации позволяет использовать дробление выходного сигнала датчика с широким диапазоном измерения параметра, охватывающего весь диапазон его изменения, на узкие интервалы изменения параметра и установление для каждого интервала своего весового коэффициента, что соответствует кусочно-линейной аппроксимации зависимости сигнала управления исполнительным двигателем от значений входных параметров. Дробление информации может быть различным: простым, когда диапазон измерения разбивается на равные интервалы; разрядным, когда диапазон измерения разбивается на разряды: единицы, десятки, сотни и т.д.; переменным, когда диапазон измерения разбивается более часто в рабочем интервале изменения параметра и менее часто в нерабочих интервалах; другие виды дробления.
Рассмотрим влияние дробления информации на скорость обучения системы управления. Допустим, сигнал управления отдельным исполнительным двигателем в j-й ситуации связан с тремя параметрами нелинейной зависимостью:
E
j = a1j + a2j2 + a3j3 .В качестве системы очувствления использованы три датчика с широким диапазоном измерения. При этом, сигнал управления будет связан с показаниями датчиков
b зависимостью:E
j = b1j + b2j2 + b3j3 .Для использования обучаемой системы управления эту зависимость необходимо привести к виду (2.1), т.е. при отсутствии дробления показаний датчиков сигнал управления определится как:
E
j = c1b1j + c2b2j + c3b3j .Процесс обучения заключается в циклическом переборе ситуаций обучаемой выборки и определении коэффициентов
ci на каждом шаге обучения по алгоритму (2.5).В обучаемую выборку входят три ситуации:
1) b11 = 3 ;
_ b21 = 2 ; _ b31 = 1 ; __ сигнал управления E1 = 8 ;Обучение считается законченным, если фактическое значение сигнала управления не выходит за пределы допустимого:
Ej + d E (принимаем d E = 0,1). Для определения степени адаптивности использованы контрольные ситуации:4) b14 = 1 ;
_ b24 = 3 ; _ b34 = 3 ; __ сигнал управления E4= 37 ;Число циклов обучения без использования дробления параметров составило:
t = 7817. Получены следующие значения весовых коэффициентов: c1 = –12,856242; c2 = 34,468731; c3 = –22,368735, которые обеспечивают следующие фактические значения сигналов управления в контрольных ситуациях: Ef4 = 1,075011; Ef5 = –15,881226.Для различных вариантов дробления информации результаты обучения имеют вид:
1 вариант.
Этот вариант дробления параметров заключается в следующем: диапазон изменения параметра разбивается на интервалы, соответствующие единице измерения параметра. Если значение параметра перекрывает данный интервал или входит в него, то значение признака, соответствующего этому интервалу, принимаем равным единице, в противном случае значение признака равно нулю.
Ситуации обучаемой выборки (верхний индекс в скобках – номер дробимого параметра, первый нижний индекс – номер полученного в результате дробления обезличенного признака, второй нижний индекс – номер ситуации):
1) b1,1(1)=1; _b2,1(1)=1; _b3,1(1)=1; _b4,1(2)=1; _b5,1(2)=1; _b6,1(2)=0; _b7,1(2)=0; _b8,1(3)=1; _b9,1(3)=0; _b10,1(3)=0; __сигнал управления E1 = 8;
2) b1,2(1)=1; _b2,2(1)=1; _b3,2(1)=1; _b4,2(2)=1; _b5,2(2)=1; _b6,2(2)=1; _b7,2(2)=0; _b8,2(3)=1; _b9,2(3)=1; _b10,2(3)=0; __сигнал управления E2 = 20;
3) b1,3(1)=1; _b2,3(1)=1; _b3,3(1)=0; _b4,3(2)=1; _b5,3(2)=1; _b6,3(2)=1; _b7,3(2)=1; _b8,3(3)=1; _b9,3(3)=1; _b10,3(3)=1; __сигнал управления E3 = 45.
Контрольные ситуации:
4)
Число циклов обучения:
t=26. Весовые коэффициенты признаков:Фактические значения сигналов управления в контрольных ситуациях:
2 вариант.
Для этого варианта дробления, как и для первого диапазон изменения параметра разбивается на интервалы, соответствующие единице изменения параметра. Если значение параметра входит в интервал, то значение признака, соответствующего этому интервалу принимаем равным единице, в противном случае значение признака равно нулю.
Ситуации обучаемой выборки для этого варианта дробления примут вид:
1) b1,1(1)=0; _b2,1(1)=0; _b3,1(1)=1; _b4,1(2)=0; _b5,1(2)=1; _b6,1(2)=0; _b7,1(2)=0; _b8,1(3)=1; _b9,1(3)=0; _b10,1(3)=0; __сигнал управления E1 = 8;
2) b1,2(1)=0; _b2,2(1)=0; _b3,2(1)=1; _b4,2(2)=0; _b5,2(2)=0; _b6,2(2)=1; _b7,2(2)=0; _b8,2(3)=0; _b9,2(3)=1; _b10,2(3)=0; __сигнал управления E2 = 20;
3) b1,3(1)=0; _b2,3(1)=1; _b3,3(1)=0; _b4,3(2)=0; _b5,3(2)=0; _b6,3(2)=0; _b7,3(2)=1; _b8,3(3)=0; _b9,3(3)=0; _b10,3(3)=1; __сигнал управления E3 = 45.
Контрольные ситуации:
Число циклов обучения:
t = 3. Весовые коэффициенты признаков:Фактические значения сигналов управления в контрольных ситуациях:
Идея дробления входной информации была изложена в заявке на изобретение ? 4242260/24 от 16 февраля 1987 г., схема которого представлена на рис.2.13.
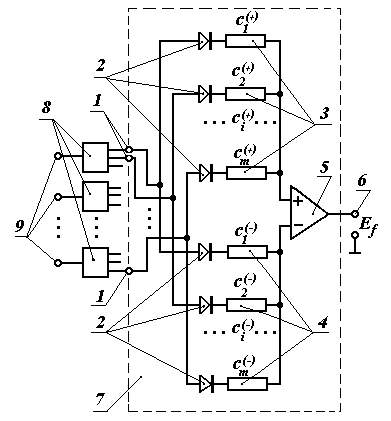
Выводы. Из рассмотренного примера видно, что дробление информации позволяет использовать линейную модель для определения сигнала управления отдельным исполнительным двигателем объекта управления, сократить продолжительность обучения, увеличить точность сигналов управления, повысить адаптивность системы управления.
2.3. Имитационное моделирование обучения системы
управления решению некоторых задач“Рефлекс цели имеет огромное жизненное значение, он есть основная форма жизненной энергии каждого из нас”
И.П.Павлов. “Рефлекс цели”
2.3.1. Имитационное моделирование процесса обучения
поиску заданного предметаОбучаемые системы управления позволяют использовать в процессе обучения не все возможные ситуации, общее количество которых может быть огромным, а только те, которые характерны для достижения поставленной перед роботом цели и необходимы по мнению обучателя. Прежде всего, в обучаемую выборку входят, очевидно, целевые ситуации, количество которых в каждой отдельной задаче невелико. Например, в задачах поиска, уклонения и в некоторых случаях автоматического регулирования (при одноэкстремальной оптимизации) используется по одной целевой ситуации, а в задачах раскладки-сортировки предметов и сборки узлов количество целевых ситуаций соизмеримо с числом обрабатываемых предметов. Кроме целевых ситуаций в обучаемую выборку должны входить некоторые другие дополнительные, опорные ситуации. Обучаемые системы управления не предъявляют жестких требований ни к выбору дополнительных ситуаций, ни к их количеству: дело обучателя – какие ситуации вводить в обучаемую выборку, а какие нет, т.е. реализуется активный метод обучения. Представляется возможным,
в качестве дополнительных принимать не только конкретные ситуации, взятые из живого опыта, но и собирательные или обобщенные ситуации [68, 73]. Рассмотрим пример использования в обучаемой выборке обобщенных ситуаций и оценим их эффективность. Допустим, требуется обучить робот поиску предмета (ключа), произвольно расположенного среди прочих предметов. Совместим технический глаз робота с его схватом. Такая схема расположения глаз, кстати, широко распространена в животном мире, особенно у хищников, которым приходится преследовать и хватать подвижную добычу. Роль схвата при этом играет пасть животного, заданной цели – его жертва.
Имитационное моделирование обучения поиску цели проведем используя вычислительную модель обучаемой системы управления.
Примем, что система очувствления робота включает 25 фотоэлектрических рецепторов сетчатки технического глаза и один датчик команды на поиск. Будем считать, что возбуждение фотоэлектрического рецептора прямо пропорционально зависит от степени затемнения его окна изображением предмета и может изменяться в пределах
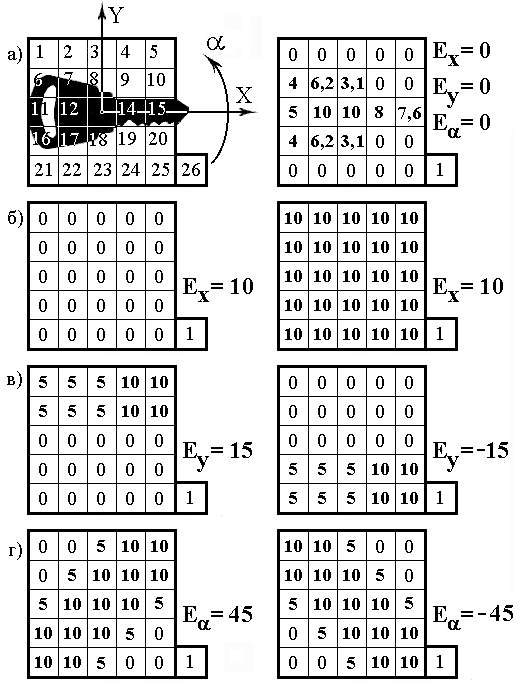
Допустимые отклонения на сигналы управления
E(x), E(y) и E(a ) в целевой ситуации должны быть малыми с тем, чтобы обеспечить точный захват предмета. В дополнительных ситуациях требования к точности сигналов управления могут быть снижены вплоть до обеспечения лишь заданного направления движения. Такое снижение требований к точности способствует сокращению длительности обучения.Таблица 2
|
Весовые коэффициенты рецепторов |
|||
|
Номер |
По оси |
По оси |
Поворот |
|
1 |
0,0913176 |
0,1363635 |
– 0,6923000 |
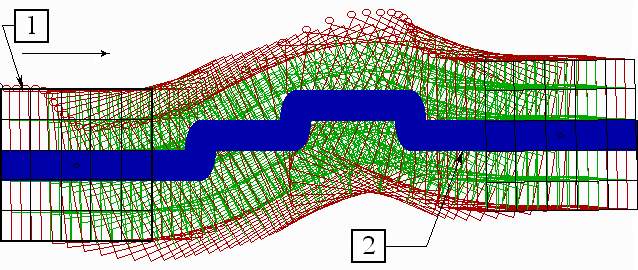
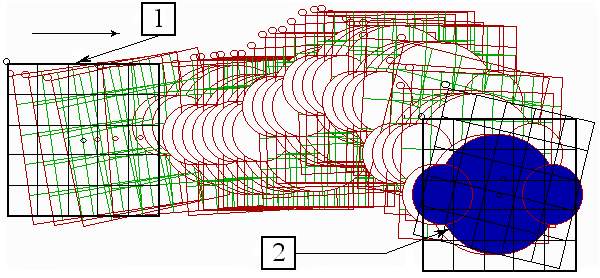
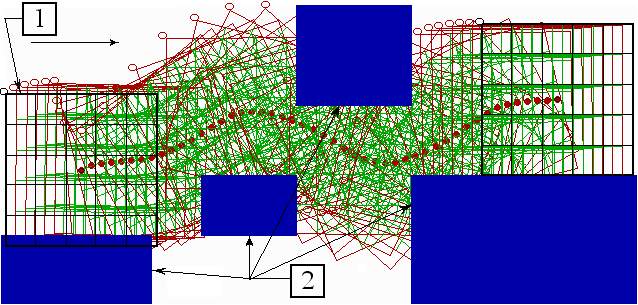
На рис.2.15 представлена стробоскопия движения технического глаза при поиске ключа. Построение выполнено следующим образом. В любом положении технического глаза определяются возбуждения
bij фоторецепторов сетчатки, вычисляются по формуле 2.1 значения сигналов управления Ej по всем осям k , и после этого технический глаз смещается на соответствующие расстояния в определенном направлении. Движение начинается с исходного, крайнего левого положения при наличии на платформе искомого предмета (b26 = 1). Для усложнения поиска на платформе находятся посторонние предметы, площадь изображения которых равна, больше или меньше площади изображения ключа.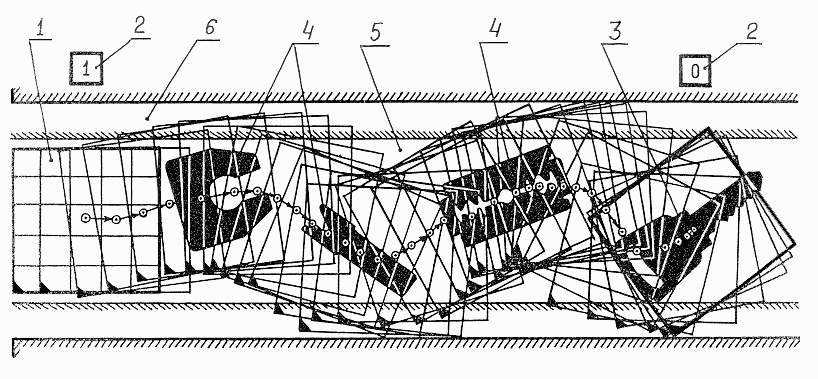
Как видно из рис.2.15, технический глаз реагирует на каждый предмет, попадающий в его поле зрения: смещается в его сторону, замедляет свою скорость при приближении к нему и ориентируется относительно его продольной оси, однако не останавливается ни на одном из искомых предметов. Только при попадании в поле зрения ключа, после необходимой ориентации, глаз останавливается. Цель достигнута.
Поиск можно повторить при ином взаимном расположении предметов, при наличии других посторонних предметов, при иной ориентации ключа, и всегда он будет успешным при условии правильного обучения.
Обучаемые системы управления могут обучаться в пассивном режиме, когда обучатель, методом “понукания” или “вождения за руку”, “натаскивает” объект управления на достижение поставленной цели в условиях реальной обстановки. Так, в рассмотренном примере поиска ключа, обучатель должен был бы в процессе обучения использовать ситуации с различными положениями искомого и посторонних предметов, с различным набором посторонних предметов и т.д. Другими словами, в обучаемую выборку должно было бы войти большое число конкретных ситуаций. При этом появление на платформе после завершения обучения иных посторонних предметов вынуждало бы обучателя в общем случае продолжать процесс обучения.
Иное дело – обучение в активном режиме, когда ситуации обучаемой выборки формируются такими, чтобы каждая из них отражала целый класс конкретных ситуаций, процесс обучения при этом значительно упрощается.
Использованные в данном примере обобщенные ситуации, за исключением, может быть, обобщенного совокупного изображения посторонних предметов, не могут быть рекомендованы на все случаи жизни, однако пример их использования говорит о целесообразности создания своего рода
Обучение выполнению задач поиска, уклонения, отслеживания и преследования, позволяет решать более сложные задачи, состоящие из различных комбинаций рассмотренных действий, например поиск и преследование цели или поиск цели с одновременным уклонением от препятствий.
2.3.2. Имитационное моделирование процесса обучения
воспроизведению образов Важной характеристикой обучаемых систем управления является их способность решать задачи воспроизведения образов.
Задача воспроизведения образа заключается в том, что в каждый момент времени уже воспроизведенная часть образа является ситуацией, которая заставляет объект управления продолжать воспроизведение остальной части образа [83]. Полностью воспроизведенный образ является целевой ситуацией в этой задаче. К таким задачам воспроизведения образа можно отнести покраску, написание знаков, изготовление деталей из заготовок и т.д.
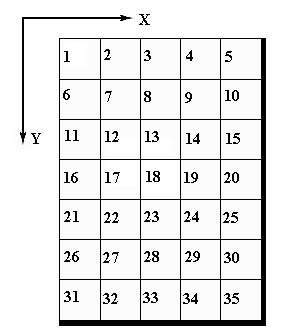
Допустим, технический глаз имеет сетчатку 5х7 рецепторов. В зависимости от степени затемнения рецептора величина возбуждения может изменяться от 0 до 100. Пронумеруем рецепторы в соответствии с рис.2.19. Для обучения используем восемь опорных (рис.2.20, а, б, в, г, д, е, ж, з) и одну целевую ситуации (рис.2.20, и). Образы этих ситуаций характеризуются наборами чисел, отражающих степень затемнения рецепторов, и расположенных в порядке нумерации рецепторов.
В качестве примера решения задачи обучения воспроизведению образа рассмотрим вычислительную модель воспроизведения изображения цифры “8”.
Обучение проведем отдельно по каждой из осей координат. Сигналы управления в ситуациях обучаемой выборки зададим таким образом, чтобы результирующее движение исполнительного органа (например руки робота с краскопультом) было направлено по траектории написания цифры “8”. Заданную точность обучения в ситуациях выборки примем равной ±
0,1 ед.

Значения возбуждений рецепторов, расположенные построчно, образуют образы ситуаций обучаемой выборки:
Образы ситуаций обучаемой выборки:
______________________________________________________________________________Сигналы1)_0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0_79__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0______10__–10 ;
2)_0__0__0__0__0_30_35__0__0__0_25_80_20__0__0__0_30_84__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0_______0__–10 ;
3)_5_60_85__0__0_37_60__2__0__0_25_80_20__0__0__0_30_84__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0______10____0 ;
4)_5_60_98_60__5_37_60__4_55_37_25_80_20__5__5__0_30_84__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0_______0___10 ;
5)_5_60_98_60__5_37_60__4_60_38_25_80_38_80_25__0_30_89_30__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0_____–10___10 ;
6)_5_60_98_60__5_37_60__4_60_38_25_80_38_80_25__0_50_95_30__0_25_80_20__0__0_30_35__0__0__0__0__0__0__0__0_______0___10 ;
7)_5_60_98_60__5_37_60__4_60_38_25_80_38_80_25__0_50_95_30__0_25_80_20__0__0_37_60__2__0__0__5_60_85__0__0______10____0 ;
8)_5_60_98_60__5_37_60__4_60_38_25_80_38_80_25__0_50_95_30__0_25_80_20__5__5_37_60__4_55_37__5_60_98_60__5_______0__–10 .
Целевая ситуация:
9)
В результате расчета по алгоритму обучения получили следующие весовые коэффициенты:
по оси
X:по оси
Y:Теперь, если поместить в начало траектории рабочий орган, то сумма весовых коэффициентов, помноженных на соответствующие возбуждения рецепторов, будет определять сигнал управления движением по отдельной координате. Перемещаясь одновременно по двум координатам, исполнительный орган будет формировать изображение, которое в свою очередь будет изменять сигналы управления двигателями в соответствии с проведенным обучением. Таким образом воспроизводится изображение цифры “8”. Похоже на то, как знаменитый Мюнхаузен сам себя вытаскивал за волосы из болота.
Процесс воспроизведения изображения цифры “8” был смоделирован на персональном компьютере. Методика моделирования заключалась в следующем. Участок экрана монитора размером 200х280 пикселей белого цвета разбиваем на 35 ячеек размером 40х40 пикселей. Задаем начальное положение черного круга радиусом 20 пикселей в центре участка. Далее следует циклический опрос ячеек. На каждом цикле считается число пикселей черного цвета в каждой ячейке, которое делится на 1600 (общее число пикселей ячейки) и умножается на 100. Получаем степень затемнения отдельной ячейки. Умножаем ее на весовой коэффициент данной ячейки для оси
X. Сложив полученные данные для всех ячеек, получаем управляющий сигнал перемещения центра черного круга по оси X. Аналогично получаем управляющий сигнал перемещения центра черного круга по оси Y. Наконец перемещаем центр круга по осям X и Y пропорционально полученным управляющим сигналам и переходим к следующему циклу опроса ячеек с учетом уже полученного затемнения ячеек. И так – многократно, пока не закончится воспроизведение образа. Все положения черного круга в ходе воспроизведения дадут стробоскопию его движения (рис.2.21).
На стробоскопии хорошо видно, как при приближении к целевой ситуации (завершении воспроизведения) уменьшается скорость движения центра черного круга и при достижении цели становится равной нулю.
Это – пример того, как компьютер был обучен именно писать заданный символ,
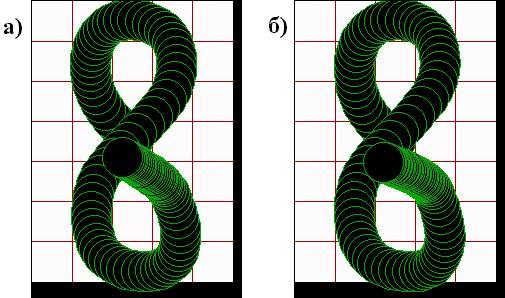
Такая компенсация погрешностей управляющих сигналов происходит потому, что управляющие сигналы по осям формирует уже воспроизведенная часть заданного образа, и отклонение этой части от заданных параметров изменяет управляющие сигналы таким образом, что траектория воспроизведения восстанавливается.
Воспроизведение изображения цифры “8” интересно тем, что в зависимости от уже воспроизведенной части образа траектория движения в средней точке (точке симметрии) имеет три различных направления.
Рассмотрим обучение воспроизведению несимметричного изображения цифры “2”.
Образы ситуаций обучаемой выборки:
_______________________________________________________________________________Сигналы1)_0__0__0__0__0__0__0__0__0__0__0_78__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0______–10__–10;
2)_3__5__0__0__0_40_50__0__0__0_15_85__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0________5__–10;
3)_7_75_85__0__0_40_65__1__0__0_15_85__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0_______10____0;
4)_7_75_98_75__7_40_65__2_55_35_15_85__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0________0___10;
5)_7_75_98_75__7_40_65__2_60_40_15_85__0_70_25__0__0__0_10__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0______–10___15;
6)_7_75_98_75__7_40_65__2_60_40_15_85__2_75_25__0__0_47_65__0__0__0_20__5__0__0__0__0__0__0__0__0__0__0__0______–10___15;
7)_7_75_98_75__7_40_65__2_60_40_15_85__2_75_25__0__0_50_65__0__0_30_85__5__0__6_90_25__0__0_10_30__0__0__0_______–5___10;
8)_7_75_98_75__7_40_65__2_60_40_15_85__2_75_25__0__0_50_65__0__0_30_85__5__0__7_90_25__0__0_40_50__0__0__0_______20____0;
9)_7_75_98_75__7_40_65__2_60_40_15_85__2_75_25__0__0_50_65__0__0_30_85__5__0__7_90_25__0__0_40_100_80_0__0_______20____0.
Целевая ситуация (рис.2.23,к):
10)
В результате расчета по алгоритму обучения получили следующие весовые коэффициенты:
по оси
X:по оси Y:
Стробоскопия воспроизведения изображения цифры “2” представлена на рис.2.23,л.

Если полученные весовые коэффициенты представить в виде оптических фильтров соответствующих участков сетчатки, степень затемнения каждого из которых пропорциональна значению его весового коэффициента, то получим негативы оптических преобразователей для воспроизведения цифр “8” (рис.2.24,а) и “2” (рис.2.24,б) в виде оптических фильтров.
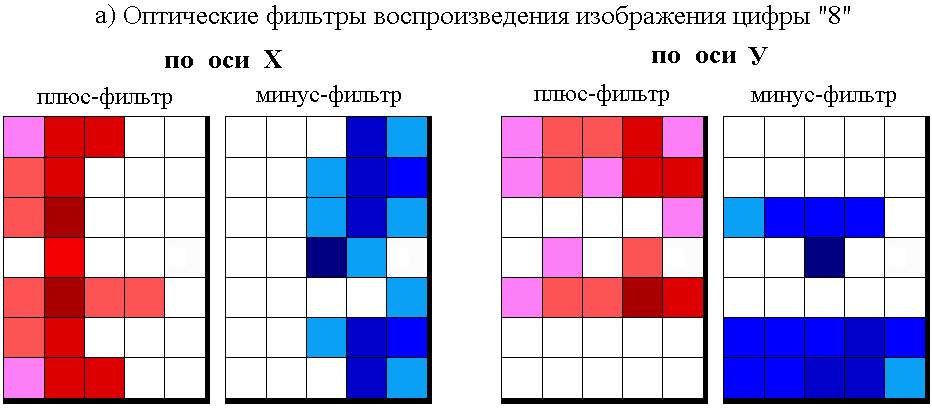
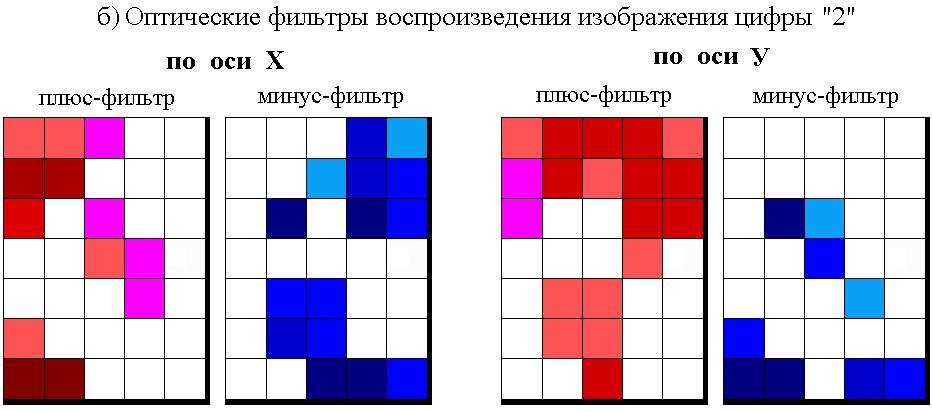
Как видно из рис.2.24, весовые коэффициенты обучаемой системы управления (резисторные или оптические) не содержат эталонов ситуаций обучаемой выборки, а отражают весь процесс обучения. Если данные оптические фильтры выполнить в виде позитивов, то они реально могут быть использованы в оптической обучаемой системе управления для воспроизведения цифр “8” и “2” (см.раздел 5.1).
Из рисунка видно так же, как обучаемые системы управления решают проблему выделения так называемых значимых и незначимых признаков, весьма сложную для теории распознавания образов. Нет необходимости заранее определять степени значимости признаков (как это делается при распознавании образов), их значимость формируется автоматически в процессе обучения. Те рецепторы, весовые коэффициенты которых, сформированные в процессе обучения, имеют большее абсолютное значение – более значимы, и наоборот. Рецепторы, весовые коэффициенты которых равны нулю, воспринимают признаки, незначимые для решения данной задачи (рецепторы 16 и 20 – для воспроизведения образа цифры “8”; рецепторы 16, 17, 20, 21, 25, 29, 30 – для воспроизведения образа цифры “2”). Причем, наличие этих рецепторов, т.е. избыточность информации, никак не влияет на способность обучаемой системы выполнять поставленную задачу.
2.3.3. Имитационное моделирование процесса обучения
распознаванию образов (ситуаций) В процессе управления подвижным объектом обучаемой системой управления процедура распознавания образов отсутствует, однако существуют задачи, для которых распознавание является конечным результатом и имеет самостоятельное значение, например в экспертных системах.
Обучаемые системы управления могут быть использованы для решения таких задач, которые относятся к задачам распознавания образов [64, 65], например для распознавания букв и цифр. Точнее будет назвать это не распознаванием, а формированием выходного сигнала, соответствующего коду образа. Рассмотрим это на примере обучения распознаванию цифр 1, 2, 3 различного написания (см.рис.2.25 а, б).
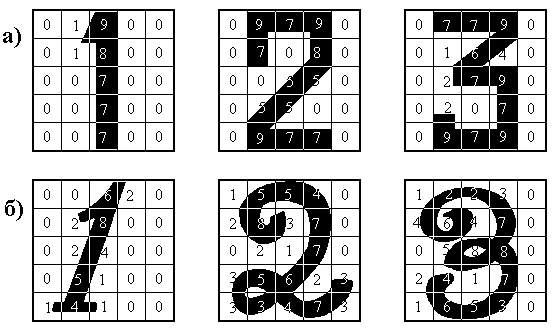
Представим изображения цифр в виде наборов чисел, характеризующих степень затемнения изображением рецепторов сетчатки 5х5. Представим полученные числа в порядке их соответствия рецепторам сетчатки – слева-направо и сверху-вниз (возможен и любой другой порядок, но одинаковый для всех изображений). Зададим для каждого изображения требуемый выходной сигнал обучаемой системы, равный значению изображенной цифры. Получим следующие ситуации обучаемой выборки:
1а)
__ 0__1__9__0__0__0__1__2__0__0__0__0__7__0__0__0__0__7__0__0__0__0__7__0__0; ___E1 = 1;Процесс обучения, проводимый в соответствии с алгоритмом обучения, будем считать законченным после того, как отклонения выходных сигналов не будут превышать значения d
E=± 0,001. Полученные значения весовых коэффициентов рецепторов сетчатки (слева-направо и сверху-вниз):
– гарантированно обеспечивают заданные значения выходных сигналов для изображений, которые использовались при обучении. Однако следует сказать, что близкие значения выходных сигналов будут получены и при других вариантах написания этих же цифр, но примерно того же размера и толщины линии. Допустимое отклонение здесь можно принять равным d
E = ± 0,5.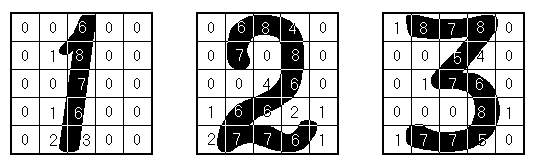
Перемножив степень затемнения каждой ячейки (рис.2.26) с ее весовым коэффициентом и просуммировав полученные 25 чисел, получим: для первого образа выходной сигнал
E=1,034477, для второго образа E=2,135356 и для третьего образа E=2,574109. Как видим, полученные значения выходных сигналов находятся в пределах допустимых значений.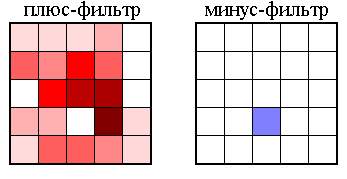
Как видно из рис.2.27, весовые коэффициенты обучаемой системы управления (резисторные или оптические) не содержат эталонов образов цифр “1”, “2” и “3”. Если данные оптические фильтры выполнить в виде позитивов, то они реально могут быть использованы в оптической обучаемой системе управления для распознавания изображений цифр “1”, “2” и “3” (см.раздел 5.1).
Следует особо отметить, что результат распознавания никак не связан с общей площадью затемнения сетчатки изображением цифры. Так для изображений цифры “3” можно задать выходной сигнал равный единице, а для изображений цифры “1” – равный трем и провести обучение системы. В результате при предъявлении изображения цифр “3”, система будет формировать выходной сигнал близкий к единице, а при предъявлении изображений цифр “1” – близкий к трем.
Способность обучаемых систем распознавать образы может быть использована для построения обучаемых экспертных систем [69]. Экспериментальный вариант такой системы был реализован в рамках хозяйственного договора “Разработка и внедрение диагностики оборудования листопрокатного производства ЛПЦ-5” между ЛипПИ и НЛМК (1987–1988 гг) при распознавании состояния узлов и деталей прокатного стана и печей обжига по их тепловым портретам, полученным с помощью тепловизора ТВ-03. Результаты работы отражены в разделе “Обучаемые системы диагностики” заключительного отчета о НИР.


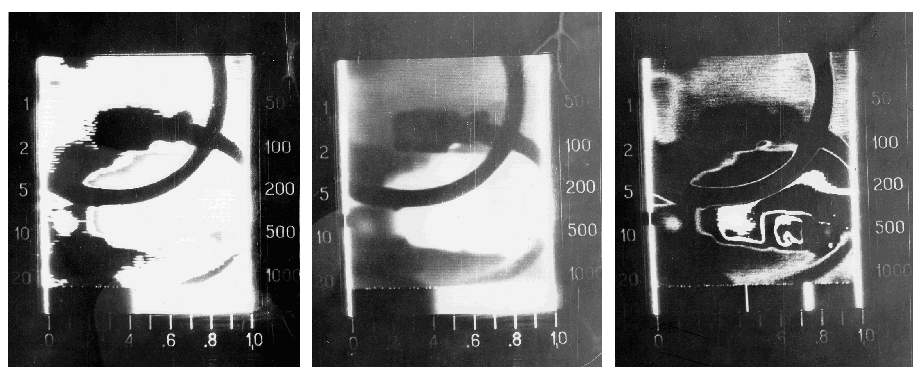
Тепловые портреты (рис.2.28) являются высоко информативными с точки зрения характеристики работы оборудования, в то же время их информация сильно зашумлена и носит избыточный характер. Обучаемые системы не чувствительны к избыточности и зашумленности информации, поэтому использование их в этом случае является эффективным.
Для каждого объекта формируется обучаемая выборка из тепловых портретов в различном его состоянии. Для каждого теплового портрета задается определенный код, который обозначает состояние объекта. Тепловые портреты разбиваются на участки, и чем мельче эти участки, тем большую точность распознавания можно получить. Для каждого участка по алгоритму обучения рассчитывается его весовой коэффициент. В процессе работы произведения степени затемненности участков помноженные на их весовые коэффициенты суммируются, и полученное значение сравнивается с набором кодов обучаемой выборки. Наиболее близкое значение кода характеризует текущее состояние объекта.
Следует отметить, что при решении задач распознавания образов обучаемые системы управления являются только частью распознающей системы, формирующей код предъявленного образа, по которому другое устройство, например компьютер, относит образ к определенному классу. Такую систему можно рассматривать как один из множества возможных вариантов систем распознавания образов.
Способность обучаемых систем управления решать задачи распознавания образов может быть использована в системе управления робота для оценки окружающей его ситуации. Это позволит, к примеру, отключать робот при попадании в его рабочую зону человека, обеспечивая его безопасность, иными словами, совершать акт управления роботом.
Таким образом, для обучаемых систем управления задача распознавания образов является частной задачей управления, но не является необходимым этапом для управления подвижным объектом в недетерминированной окружающей его обстановке.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|